平衡搜尋樹(AVL樹)
AVL樹是由GM Adelson - Velsky和EM Landis於1962年發明的。為了紀念其發明者,這樹結構被命名為AVL。
AVL樹可以定義為高度平衡二元搜尋樹,其中每個節點與平衡因子相關聯,該平衡因子通過從其左子樹的子樹中減去其右子樹的高度來計算。
如果每個節點的平衡因子在-1到1之間,則稱樹是平衡的,否則,樹將是不平衡的並且需要平衡。
平衡係數(k)=高度(左(k)) - 高度(右(k))
如果任何節點的平衡因子為1,則意味著左子樹比右子樹高一級。
如果任何節點的平衡因子為0,則意味著左子樹和右子樹包含相等的高度。
如果任何節點的平衡因子是-1,則意味著左子樹比右子樹低一級。
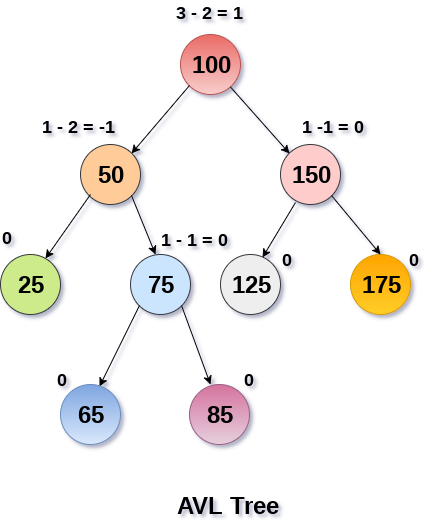
AVL樹如下圖所示。 可以看到,與每個節點相關的平衡因子介於-1和+1之間。 因此,它是AVL樹的一個例子。
複雜性
| 演算法 | 平均情況 | 最壞情況 |
|---|---|---|
| 空間 | o(n) | o(n) |
| 搜尋 | o(log n) | o(log n) |
| 插入 | o(log n) | o(log n) |
| 刪除 | o(log n) | o(log n) |
AVL樹上的操作
由於AVL樹也是二元搜尋樹,所有操作都以與在二元搜尋樹中執行的相同方式執行。 搜尋和遍歷不會導致AVL樹違反屬性。 但是,插入和刪除操作可能會違反此屬性,因此樹可能需要平衡。
| 編號 | 操作 | 說明 |
|---|---|---|
| 1 | 插入 | AVL樹中的插入的執行方式與在二元搜尋樹中執行的方式相同。但是,它可能會導致違反AVL樹屬性,因此樹可能需要平衡。可以通過應用旋轉來平衡樹。 |
| 2 | 刪除 | 刪除也可以按照在二元搜尋樹中執行的相同方式執行。 刪除也可能會擾亂樹的平衡,因此,使用各種型別的旋轉來重新平衡樹。 |
為什麼要使用AVL樹
AVL樹通過不讓它傾斜來控制二元搜尋樹的高度。 高度為h的二元搜尋樹中的所有操作所花費的時間是O(h)。 但是,如果二元搜尋樹變得偏斜(即最壞的情況),它可以擴充套件到O(n)。 通過將該高度限制為log n,AVL樹將每個操作的上限強加為O(log n),其中n是節點的數量。