在平衡搜尋樹中刪除元素

從AVL樹中刪除節點類似於二元搜尋樹中刪除節點。 刪除可能會干擾AVL樹的平衡因子，因此需要重新平衡樹以保持AVL樹平衡。 因此需要進行旋轉。 兩種型別的旋轉是L旋轉和R旋轉。 在這裡將討論R旋轉。L旋轉是它們的映象。

如果要刪除的節點存在於關鍵節點的左子樹中，則需要應用L旋轉，否則，如果要刪除的節點存在於關鍵節點的右子樹中 ，將執行R旋轉。

考慮一下，A是關鍵節點，B是其左子樹的根節點。 如果要刪除存在於A的右子樹中的節點X，則可能存在三種不同的情況：

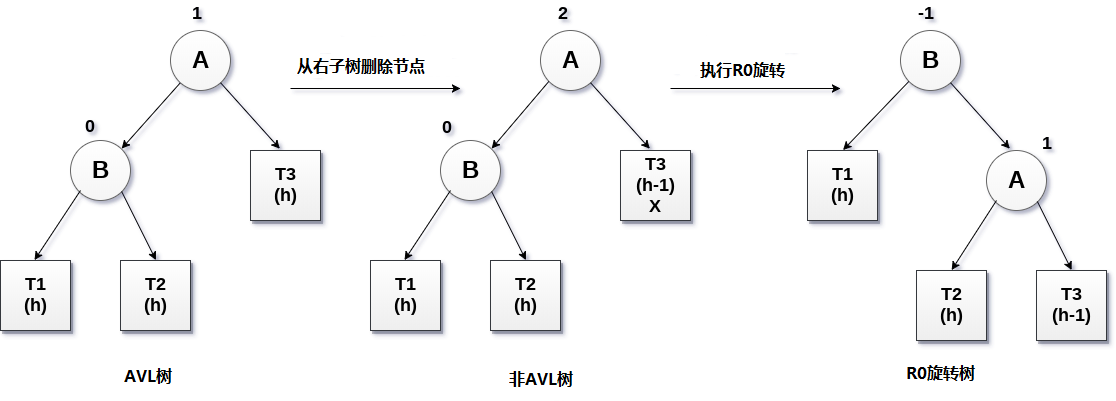
1. R0旋轉(節點B的平衡係數為0)

如果節點B具有0平衡因子，並且在刪除節點X時節點A的平衡因子受到干擾，則將通過使用R0旋轉旋轉樹來重新平衡樹。

關鍵節點A向右移動，節點B成為樹的根，T1為左子樹。 子樹T2和T3成為節點A的左右子樹，R0旋轉中涉及的過程如下圖所示。

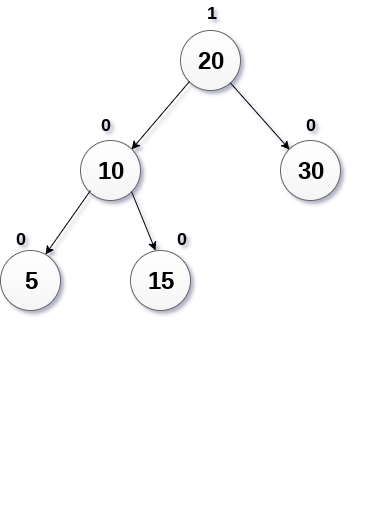
範例：
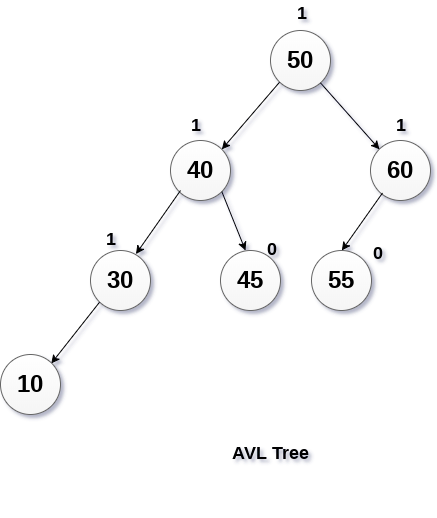
從下圖中顯示的AVL樹中刪除節點30。

解釋

在這種情況下，節點B具有平衡因子0，因此將通過使用R0旋轉來旋轉樹，如下圖所示。 節點B(10)成為根，而節點A向右移動。 節點B的右子節點現在將成為節點A的左子節點。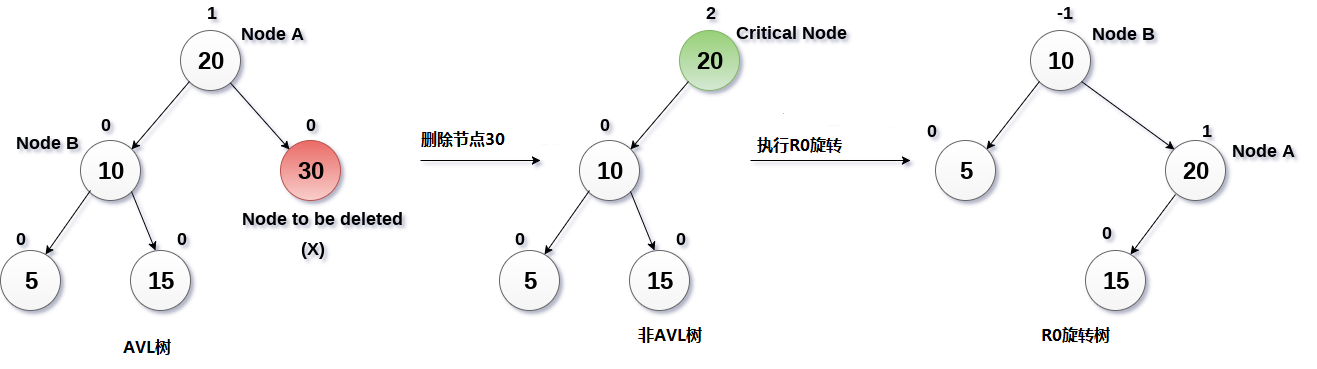

2. R1旋轉(節點B具有平衡因子1)

如果節點B的平衡因子是1，則執行R1旋轉。在R1旋轉中，關鍵節點A向右移動，子樹T2和T3分別作為其左和右子節點。 T1將被放置為節點B的左子樹。

R1旋轉涉及的過程如下圖所示。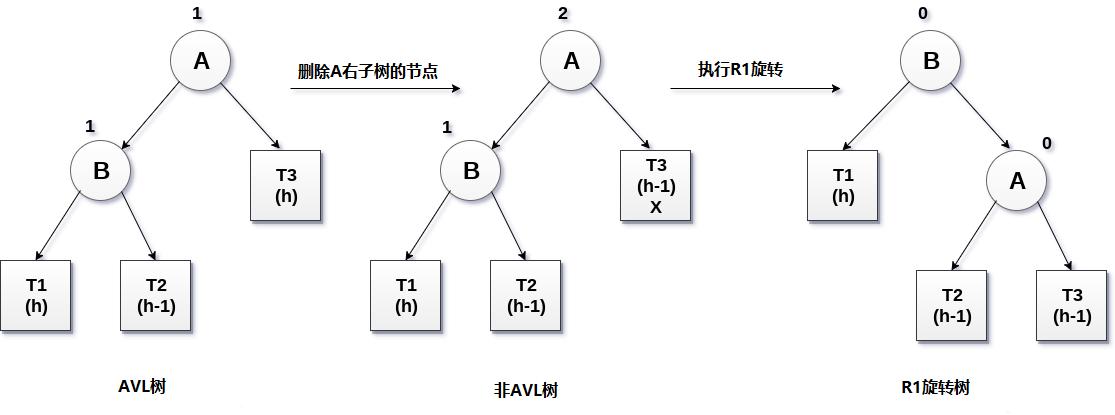

範例

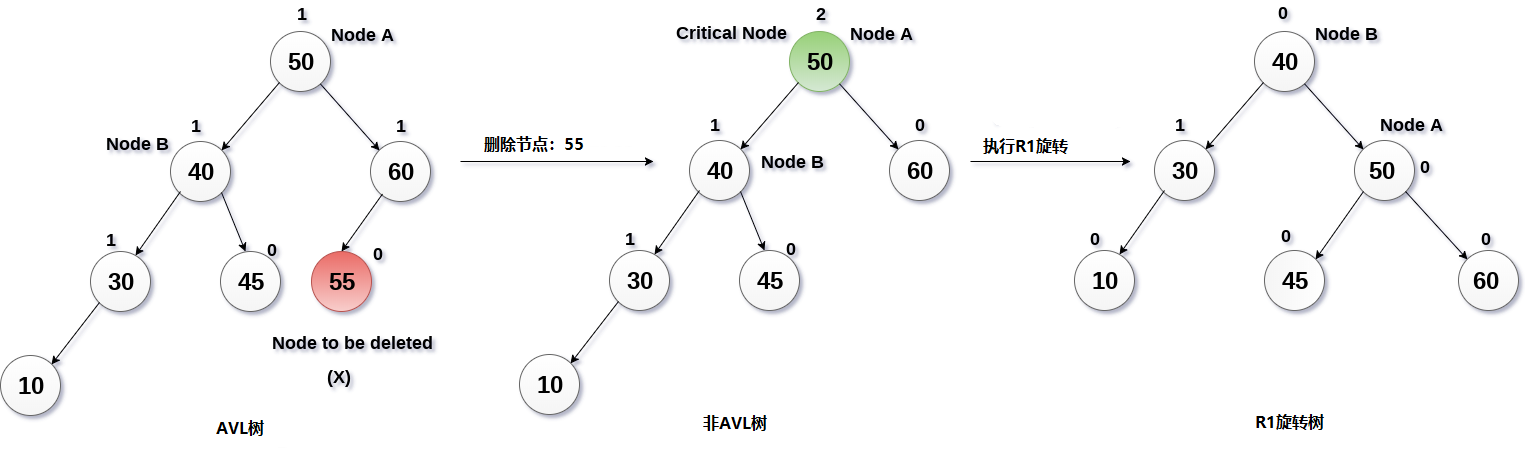
從下圖中顯示將要刪除AVL樹中的節點55。

方案：

從AVL樹中刪除55節點，擾亂了節點50的平衡因子，即成為關鍵節點的節點A. 這是R1旋轉的條件，其中節點A將向右移動(如下圖所示)。 B的右側現在變為A的左邊(即45)。

解決方案中涉及的過程如下圖所示。

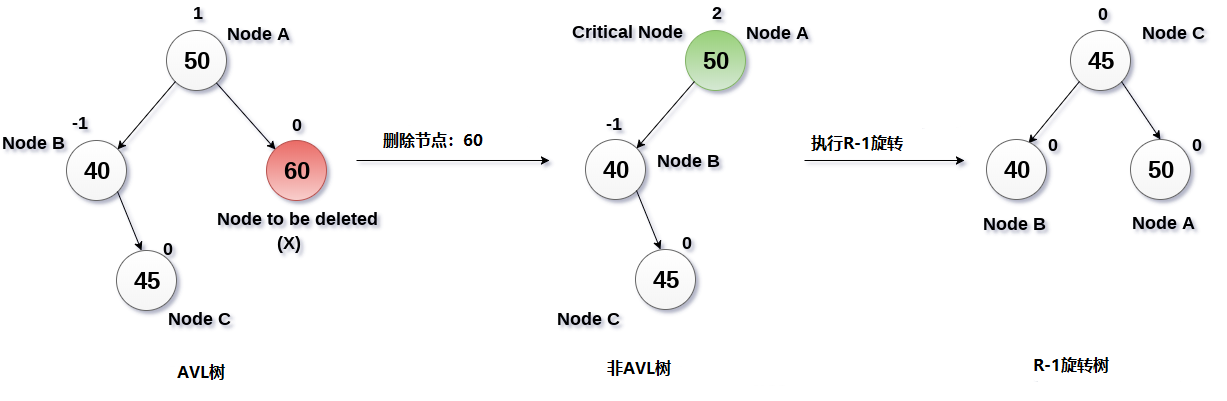
3. R-1旋轉(節點B具有平衡因子-1)

如果節點B具有平衡因子-1，則執行R-1旋轉。 這種情況的處理方式與LR旋轉相同。 在這種情況下，作為節點B的右子節點的節點C成為樹的根節點，其中B和A分別作為其左和右子節點。

子樹T1，T2成為B的左右子樹，而T3，T4成為A的左右子樹。

R-1旋轉涉及的過程如下圖所示。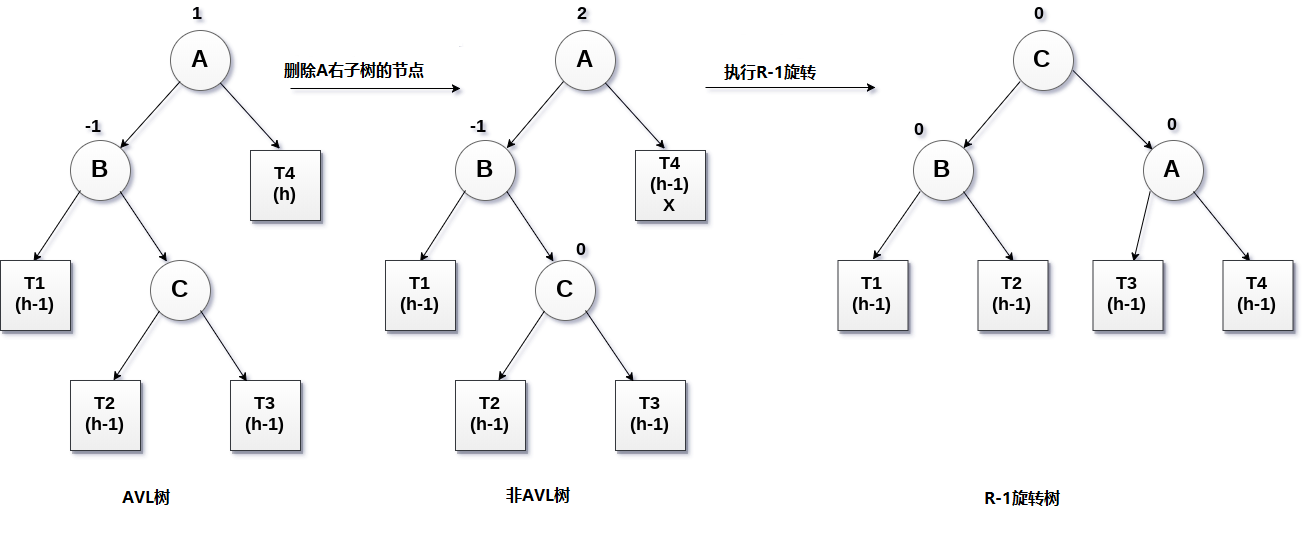

範例

從下圖所示的AVL樹中刪除節點60。

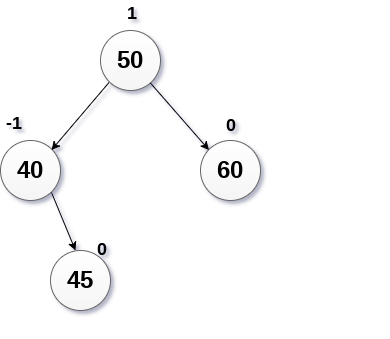
解答：

在這種情況下，節點B具有平衡因子-1。 因此，刪除節點60會擾亂節點50的平衡因子，需要執行R-1旋轉。 節點C即45成為樹的根，節點B(40)和A(50)作為其左右子節點。