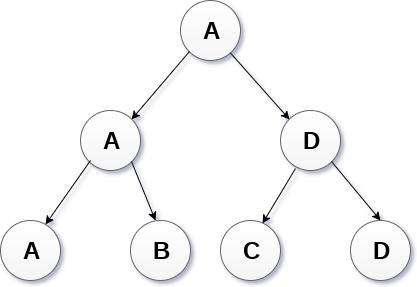
樹

• 樹是一種遞回資料結構，包含一個或多個資料節點的集合，其中一個節點被指定為樹的根，而其餘節點被稱為根的子節點。
• 除根節點之外的節點被劃分為非空集，其中每個節點將被稱為子樹。
• 樹的節點要麼保持它們之間的父子關係，要麼它們是姐妹節點。
• 在通用樹中，一個節點可以具有任意數量的子節點，但它只能有一個父節點。
• 下圖顯示了一棵樹，其中節點A是樹的根節點，而其他節點可以看作是A的子節點。

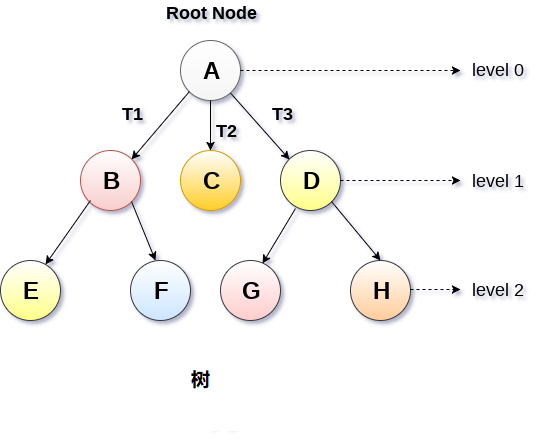
基本術語

• 根節點 ： 根節點是樹層次結構中的最頂層節點。 換句話說，根節點是沒有任何父節點的節點。
• 子樹： 如果根節點不為空，則樹T1，T2和T3稱為根節點的子樹。
• 葉節點： 樹的節點，沒有任何子節點，稱為葉節點。 葉節點是樹的最底部節點。 一般樹中可以存在任意數量的葉節點。 葉節點也可以稱為外部節點。
• 路徑： 連續邊的序列稱為路徑。 在上圖所示的樹中，節點E的路徑為A→B→E。
• 祖先節點： 節點的祖先是從根到該節點的路徑上的任何前節點。根節點沒有祖先節點。 在上圖所示的樹中，節點F的祖先是B和A。
• 度： 節點的度數等於子節點數，節點數。 在上圖所示的樹中，節點B的度數為2。葉子節點的度數總是0，而在完整的二元樹中，每個節點的度數等於2。
• 級別編號： 為樹的每個節點分配一個級別編號，使得每個節點都存在於高於其父級的一個級別。樹的根節點始終是級別0。

樹的靜態表示

#define MAXNODE 500
struct treenode {
    int root;
    int father;
    int son;
    int next;
}

樹的動態表示

struct treenode
{
    int root;  
    struct treenode *father;
    struct treenode *son
    struct treenode *next;
}

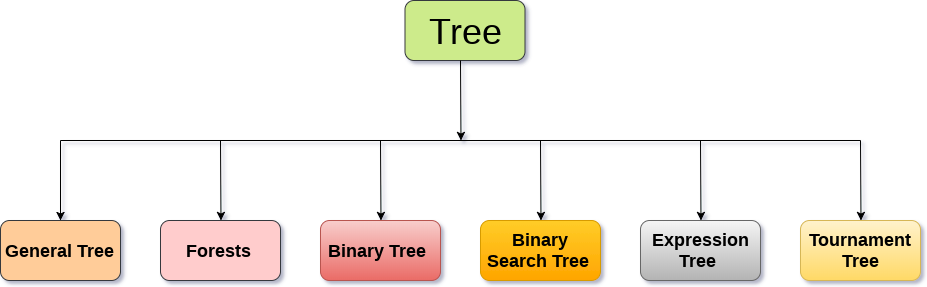
樹的型別

樹資料結構可以分為六個不同的類別。

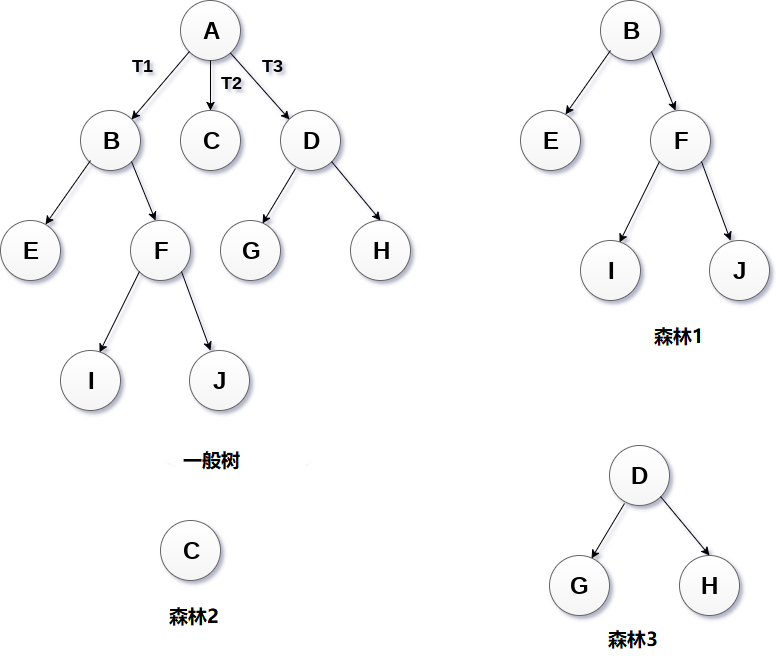
1.一般樹

一般樹(General Tree)按層次順序儲存元素，其中頂級元素始終以0級作為根元素。 除根節點之外的所有節點都以級別數存在。 存在於同一級別的節點稱為兄弟節點，而存在於不同級別的節點表現出它們之間的父子關係。 節點可以包含任意數量的子樹。 每個節點包含3個子樹的樹稱為三元樹。

2.森林

可以將森林(Forests)定義為可以通過刪除根節點並將根節點連線到第一級節點的邊緣來獲得的不相交樹的集合。

3.二元樹

二元樹是一種資料結構，其中每個節點最多可以有2個子節點。 存在於最頂層的節點稱為根節點。 具有0個子節點的節點稱為葉節點。 二元樹用於表示式評估等應用程式。 我們將在本教學後面詳細討論二元樹。

4.二元搜尋樹

二元搜尋樹是有序二元樹。 左子樹中的所有元素都小於根，而右子樹中存在的元素大於或等於根節點元素。 二進位制搜尋樹用於電腦科學領域的大多數應用，如搜尋，排序等。

5.表達樹

表示式樹用於評估簡單的算術表示式。表示式樹基本上是二元樹，其中內部節點由運算子表示，而葉節點由運算元表示。表示式樹被廣泛用於解決代數表示式，如(a + b)*(a-b)。 請考慮以下範例。

使用以下代數表示式構造表示式樹:

(a + b) / (a*b - c) + d

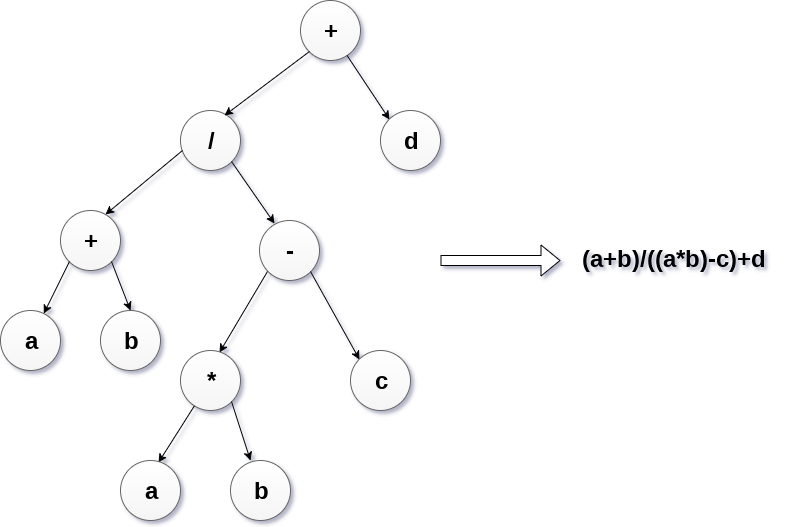
6.競賽樹

競賽樹用於記錄兩名比賽者之間每輪比賽的勝者。 比賽樹也可以稱為選擇樹或獲勝者樹。 外部節點表示正在播放匹配的比賽者，而內部節點表示所播放的匹配的勝者。 在最頂層，比賽的獲勝者作為樹的根節點出現。

例如，在4個比賽者之間進行的比賽樹如下所示。 但是，左子樹中的獲勝者將與右子樹的獲勝者對戰。