資料結構漸近分析
在數學分析中,演算法的漸近分析是一種定義執行時效能的數學邊界的方法。 使用漸近分析,可以很容易地得出關於演算法的平均情況,最佳情況和最壞情況的結論。
它用於計算演算法內任何操作的執行時間。
範例:一個操作的執行時間為x(n),另一個操作的執行時間計算為f(n2)。 它指的是執行時將隨著第一次操作n的增加而線性增加,並且執行時間將以指數方式增加以進行第二次操作。 類似地,如果n非常小,則兩個操作的執行時間將相同。
通常,演算法所需的時間有三種型別:
- 最壞情況:它定義了演算法占用大量時間的輸入。
- 平均情況:程式執行需要平均時間。
- 最佳情況:它定義演算法佔用最少時間的輸入。
漸近符號
用於計算演算法執行時複雜度的常用漸近符號,如下:
- 大歐符號(Ο)
- 歐米茄符號(Ω)
- 西塔表示法(θ)
大歐符號(Ο)
它是表達演算法執行時間上限的正式方法,它測量時間複雜度的最壞情況或最長時間,演算法完成其操作所需的時間。 它表示如下: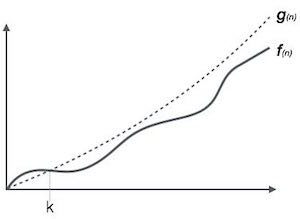
歐米茄符號(Ω)
它是表示演算法執行時間下限的正式方法。 它衡量演算法可能完成的最佳時間量或最佳的案例時間複雜度。
如果要求演算法在不使用上限的情況下花費至少一定的時間,使用大Ω表示法,即希臘字母「omega」。它用於限制輸入大小的執行時間的增長。
如果執行時間是Ω(f(n)),則對於較大的n值,對於常數(k),執行時間至少為k * f(n)。 它表示如下:
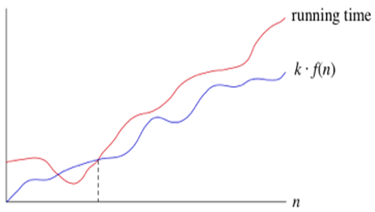
西塔符號(θ)
它是表達演算法執行時間的上限和下限的正式方式。
考慮演算法的執行時間是θ(n),如果一次(n)變得足夠大,則對於某些常數k1和k2,執行時間最多為k2-n並且至少為k1≤n。 它表示如下:
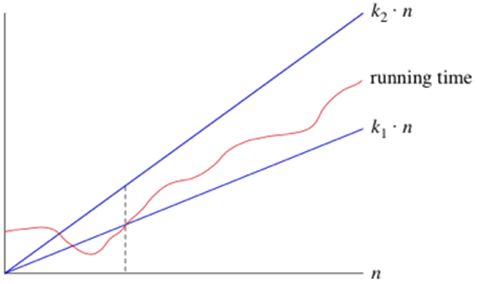
常見的漸近符號
| 變數 | ?(1) |
|---|---|
| 線性 | ?(n) |
| 對數 | ?(log n) |
| n log n | ?(n log n) |
| 指數 | 2?(n) |
| 立方 | ?(n3) |
| 多項式 | n?(1) |
| 二次方 | ?(n2) |