在平衡搜尋樹中插入元素
2019-10-16 22:02:20
AVL樹中的插入的執行方式與在二元搜尋樹中執行的方式相同。 新節點作為葉節點新增到AVL樹中。 但是,它可能會導致違反AVL樹屬性,因此樹可能需要平衡。
可以通過應用旋轉來平衡樹。 僅當插入新節點時任何節點的平衡因子受到干擾時才需要旋轉,否則不需要旋轉。
根據插入的型別,旋轉分為四類。
| 編號 | 旋轉 | 描述 |
|---|---|---|
| 1 | LL旋轉 | 新節點被插入到關鍵節點的左子樹的左子樹中。 |
| 2 | RR旋轉 | 新節點被插入到關鍵節點的右子樹的右子樹中。 |
| 3 | LR旋轉 | 新節點被插入到關鍵節點的左子樹的右子樹中。 |
| 4 | RL旋轉 | 新節點被插入到關鍵節點的右子樹的左子樹中。 |
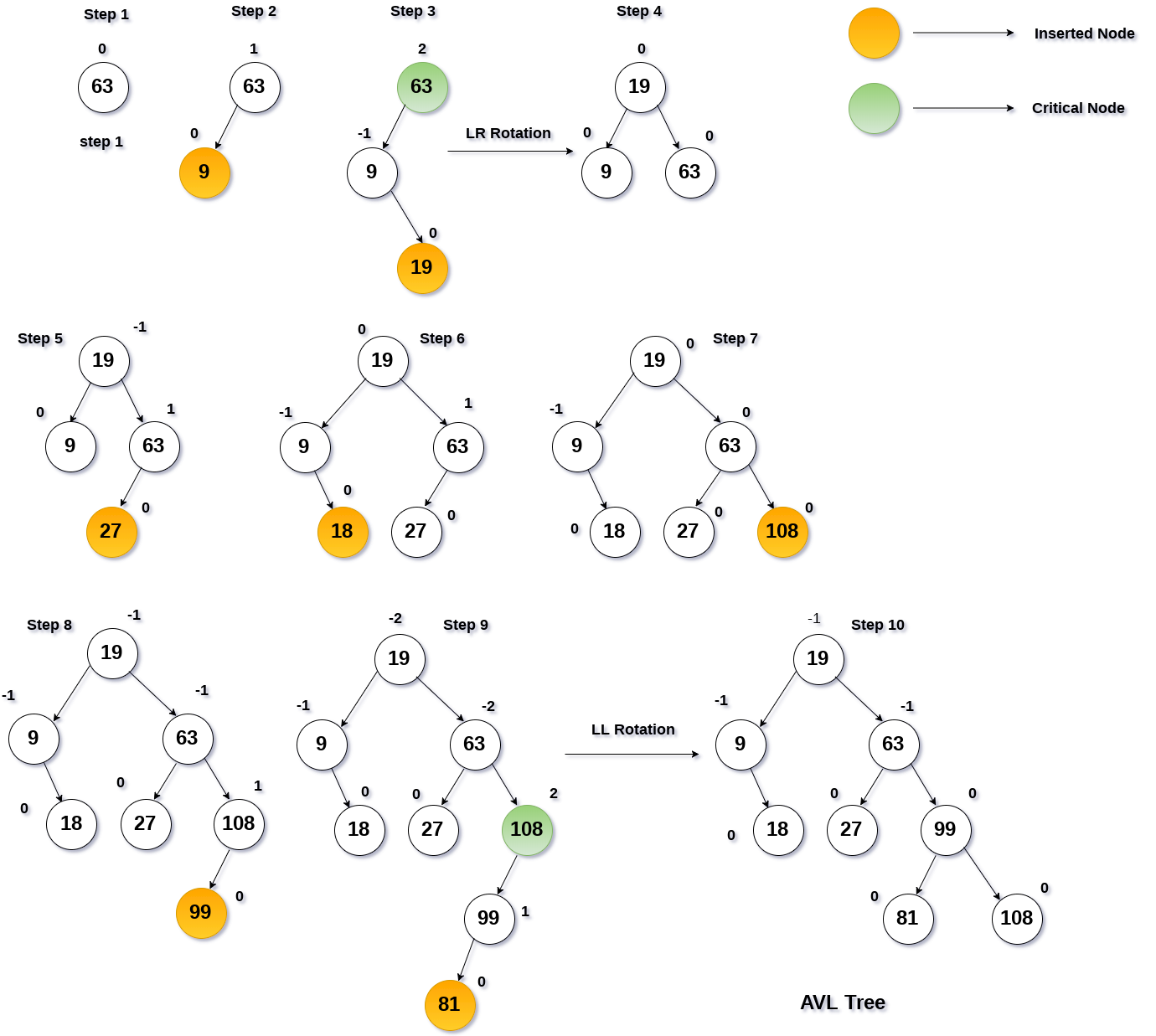
範例: 通過以給定順序插入以下元素來構造AVL樹。
63, 9, 19, 27, 18, 108, 99, 81
從給定元素集構造AVL樹的過程如下圖所示。
在每一步,必須計算每個節點的平衡因子,如果發現它大於2或小於-2,那麼需要一個旋轉來重新平衡樹。 旋轉型別將通過插入元素相對於關鍵節點的位置來估計。
插入所有元素以維持二元搜尋樹的順序。