左左（LL）旋轉

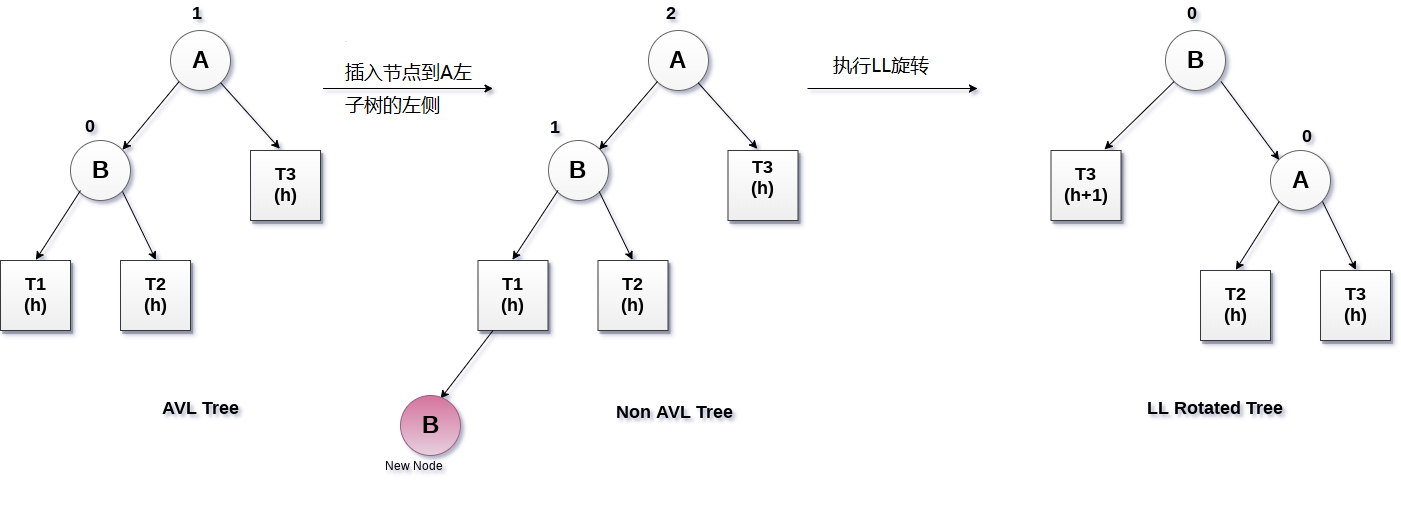
下圖所示的樹是AVL樹，但是，需要在A的左子樹的左側插入一個元素。樹可能會因關鍵節點A的存在而變得不平衡。

平衡因子不在-1和1之間的節點稱為關鍵節點。要重新平衡樹，執行LL旋轉，如下圖所示。

節點B成為根，A和T3作為其左右子節點。 T1和T2成為A的左右子樹。

範例：

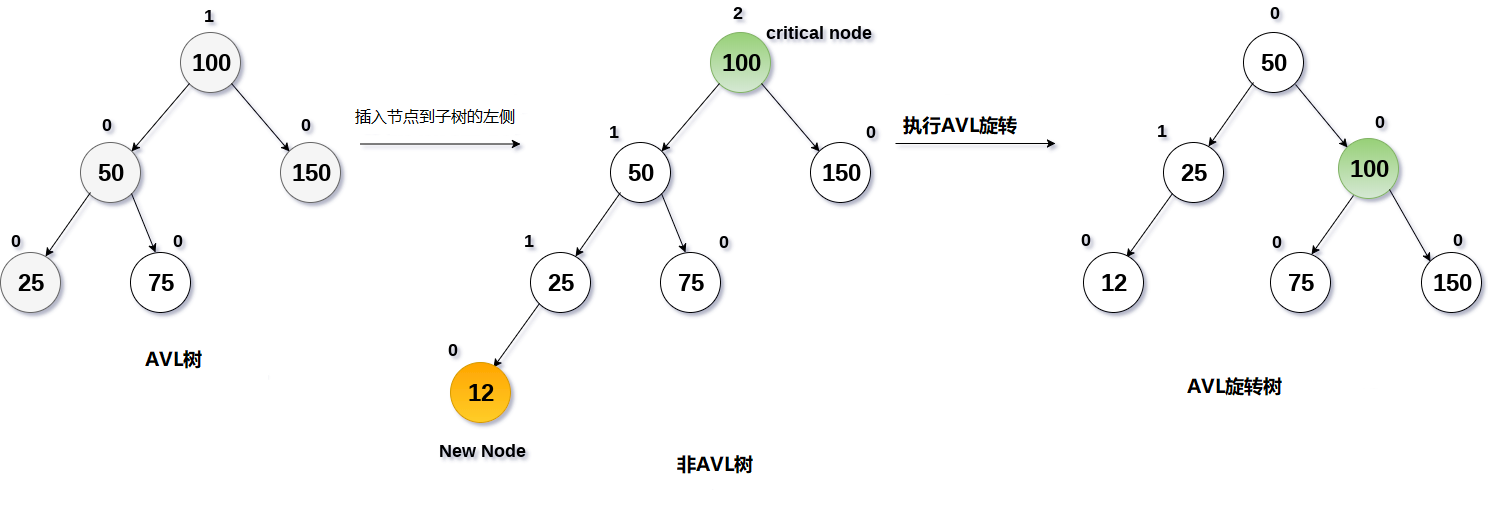
將值為12的節點插入下圖所示的樹中。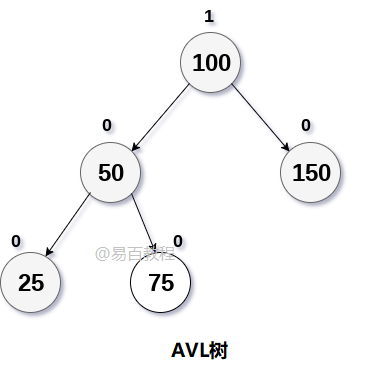

解決：
12將被插入25的左側，因此，它擾亂了AVL樹的平衡。 樹需要通過LL旋轉旋轉來重新平衡。

這裡，關鍵節點100將移動到其右側，並且其左子樹(B)的根將是樹的新根節點。

B的右子樹，即T2(具有根節點75)將位於節點A的左側(值為100)。

通過遵循此過程，樹將被重新平衡，因此，它將是在插入12之後生成的AVL樹。