左右（LR）旋轉

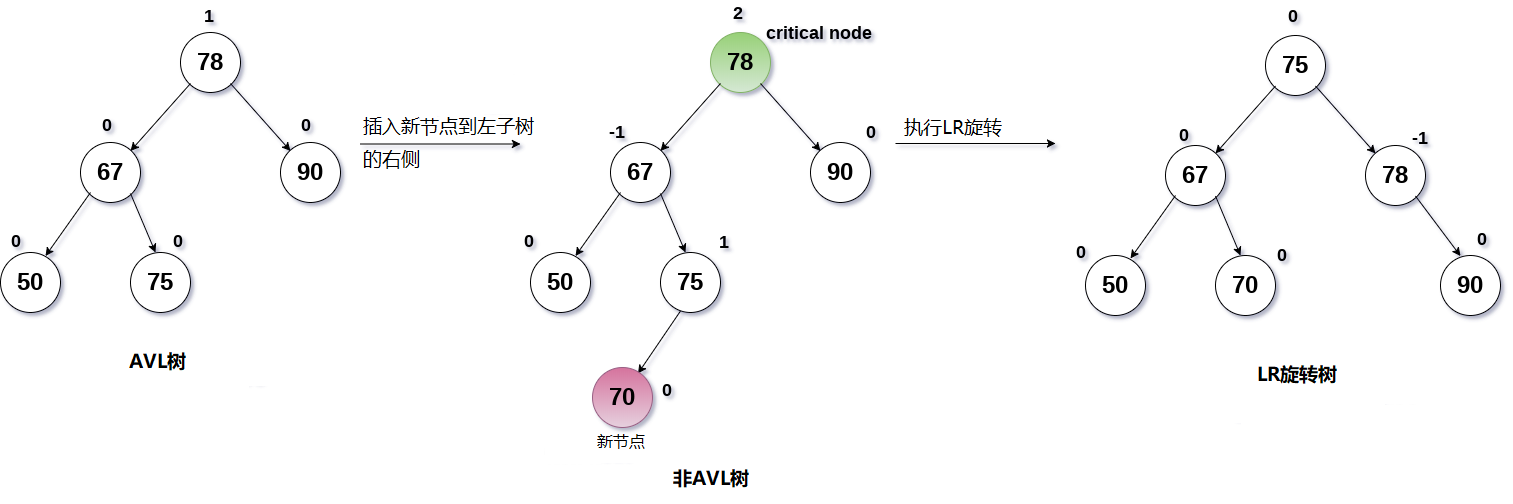
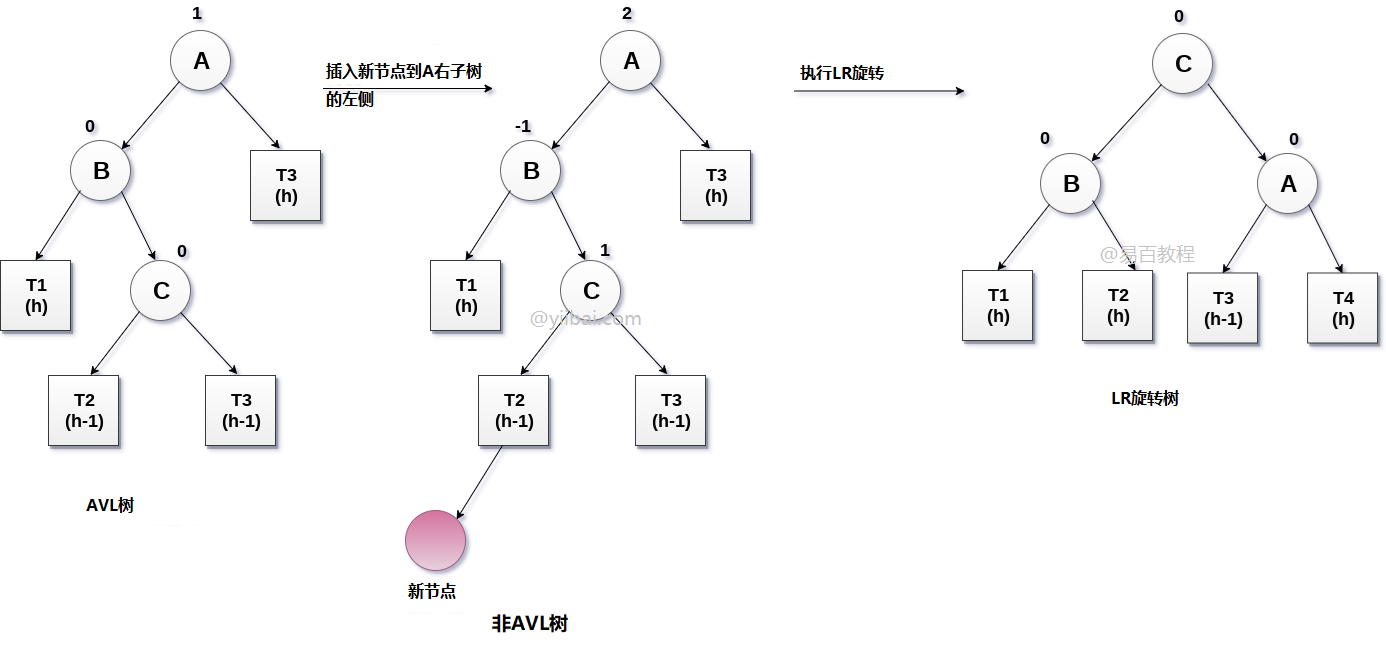
如果將新節點插入節點A的左子樹的右側，則執行LR旋轉。

在LR旋轉中，節點C(如圖所示)成為樹的根節點，而節點B和A分別成為其左右子節點。

T1和T2分別成為節點B的左右子樹，而T3和T4成為節點A的左右子樹。

範例：

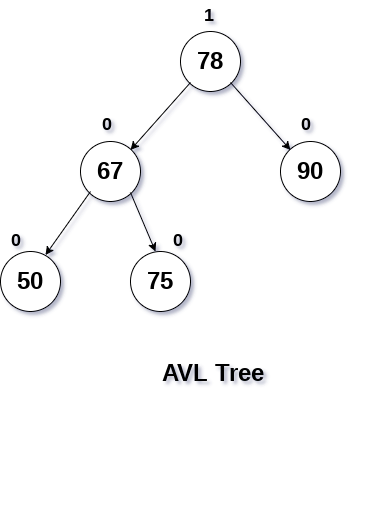
將值為70的節點插入到以下資料結構顯示的樹中。

解決方案：

根據二元搜尋樹的屬性，將值為70的節點插入到樹根的左子樹的右側。

如圖所示，插入70時根節點的平衡因子受到干擾，這成為關鍵節點A。

要重新平衡樹，將執行LR旋轉。 節點C即75將成為樹的新根節點，其中B和A分別作為其左和右子節點。

子樹T1，T2成為B的左右子樹，而子樹T3，T4成為A的左右子樹。

該過程如下圖所示。