遞回基礎知識

一些計算機程式設計語言允許一個模組或函式來呼叫自身。這種技術被稱為遞回。在遞回函式α直接呼叫自己或呼叫函式β，反過來呼叫原函式α。該函式α被稱為遞回函式。

特性

遞回函式可以無限執行就類似一個迴圈。為了避免遞回函式的無窮執行，一個遞回函式必須具備有兩個屬性 -

• 基本準則 ? 必須有至少一個基本的標準或條件，例如，當滿足此條件時函式停止遞回呼叫自身。

• 由淺入深 ? 遞回呼叫應該在那個遞迴呼叫作出每次涉及靠近基標準這樣的方式前進。

實現

許多程式設計語言通過堆疊的方式實現遞回。一般來說，當一個函式（呼叫者）呼叫另一個函式（被呼叫者）或本身作為被呼叫， 呼叫者傳送函式執行控制權被呼叫。

這意味著，呼叫方函式具有暫停其執行並在稍後繼續時從被呼叫函式的執行控制返回。在這裡，呼叫函式需要從執行的角度入手正是它把自己擱置。它也需要完全相同的資料值執行。為此，活動記錄（或堆疊影格）可以建立呼叫函式。

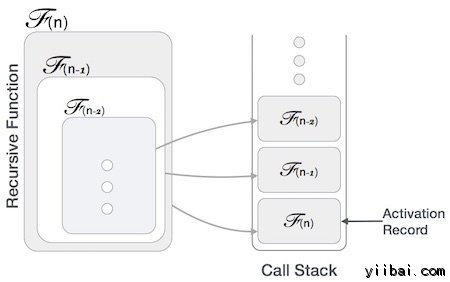
此活動記錄保留區域性變數的資訊，形式引數，返回地址並傳遞給呼叫函式的所有資訊。

遞回分析

有人可能會認為，作為同樣的任務可以反復地來完成，為什麼使用遞迴？第一個原因是遞迴使得程式更具可讀性，並因為今天的提升 CPU 系統中，遞回比迭代更加高效。

時間複雜度

如果是疊代，我們採取疊代次數來計算的時間複雜度。同樣，在遞回的情況下，假設一切都不變，我們試著找出遞回呼叫的次數。 呼叫一個函式是 Ο(1), 因此（n）數量是遞迴呼叫作出遞回函式的時間 Ο(n)。

空間複雜度

空間複雜度是算作所需要的執行模組的額外空間量。如遇迭代，編譯器幾乎不要求任何額外的空間。 編譯器不斷更新並反復使用的變數值。 但如遇到遞迴，系統需要的遞迴呼叫作出每次儲存啟用記錄。因此可以認為，空間遞回函式的複雜性可能比用疊代的函式去更高。