佇列優先順序

優先順序佇列比佇列更專業的資料結構。像普通佇列，優先順序佇列中有相同的方法，但在使用上是有比較大的區別的。在優先順序佇列資料項都受到鍵值排序，以便與最低鍵的值，資料項在前方，鍵的最高值的資料項在後方，反之亦然。因此，我們根據它的鍵值分配的優先項。數值越低，優先順序越高。以下是優先順序佇列的主要方法。

基本操作

• 插入/入隊 ? 增加資料項到佇列的後部。

• 刪除/出隊 ? 從佇列的前面刪除一個資料項。

優先順序佇列表示

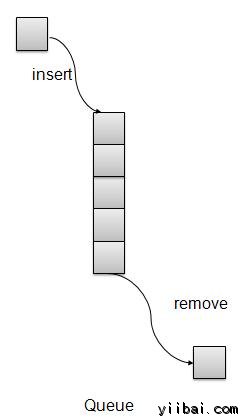
我們將在本文中使用陣列來實現佇列。還有一些通過佇列支援更多的操作如下。

• Peek ? 獲得在佇列前面的元素。

• isFull ? 檢查佇列是否已滿。

• isEmpty ? 檢查佇列是否為空。

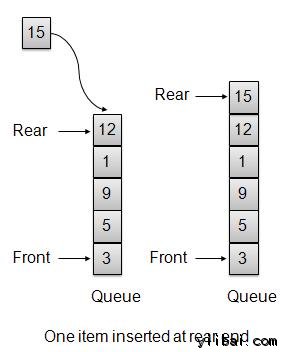
插入/入隊操作

每當一個元素被插入佇列時，優先順序佇列根據其順序插入對應的資料項。在這裡，我們假設高值的資料具有低優先順序。

void insert(int data){
   int i = 0;

   if(!isFull()){
      // if queue is empty, insert the data 
		
      if(itemCount == 0){
         intArray[itemCount++] = data;        
      }else{
         // start from the right end of the queue 
         for(i = itemCount - 1; i >= 0; i-- ){
            // if data is larger, shift existing item to right end 
            if(data > intArray[i]){
               intArray[i+1] = intArray[i];
            }else{
               break;
            }            
         }   
         // insert the data 
         intArray[i+1] = data;
         itemCount++;
      }
   }
}

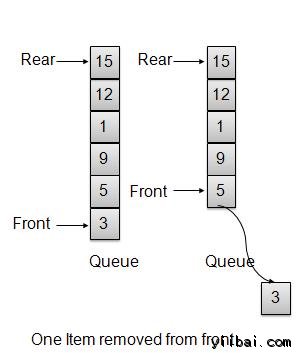
刪除/解列操作

每當一個元素是從佇列中刪除，佇列使用專案計數得到元素。一旦元素被移除，專案計數減一。

int removeData(){
   return intArray[--itemCount]; 
}

演示程式

PriorityQueueDemo.c

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6

int intArray[MAX];
int itemCount = 0;

int peek(){
   return intArray[itemCount - 1];
}

bool isEmpty(){
   return itemCount == 0;
}

bool isFull(){
   return itemCount == MAX;
}

int size(){
   return itemCount;
}  

void insert(int data){
   int i = 0;

   if(!isFull()){
      // if queue is empty, insert the data 
      if(itemCount == 0){
         intArray[itemCount++] = data;        
      }else{
         // start from the right end of the queue 
			
         for(i = itemCount - 1; i >= 0; i-- ){
            // if data is larger, shift existing item to right end 
            if(data > intArray[i]){
               intArray[i+1] = intArray[i];
            }else{
               break;
            }            
         }  
			
         // insert the data 
         intArray[i+1] = data;
         itemCount++;
      }
   }
}

int removeData(){
   return intArray[--itemCount]; 
}

int main() {
   /* insert 5 items */
   insert(3);
   insert(5);
   insert(9);
   insert(1);
   insert(12);

   // ------------------
   // index : 0  1 2 3 4 
   // ------------------
   // queue : 12 9 5 3 1 
   insert(15);

   // ---------------------
   // index : 0  1 2 3 4  5 
   // ---------------------
   // queue : 15 12 9 5 3 1
	
   if(isFull()){
      printf("Queue is full!\n");   
   }

   // remove one item 
   int num = removeData();
   printf("Element removed: %d\n",num);
	
   // ---------------------
   // index : 0  1  2 3 4 
   // ---------------------
   // queue : 15 12 9 5 3  

   // insert more items
   insert(16);

   // ----------------------
   // index :  0  1 2 3 4  5
   // ----------------------
   // queue : 16 15 12 9 5 3

   // As queue is full, elements will not be inserted. 
   insert(17);
   insert(18);

   // ----------------------
   // index : 0   1  2 3 4 5
   // ----------------------
   // queue : 16 15 12 9 5 3
   printf("Element at front: %d\n",peek());

   printf("----------------------\n");
   printf("index : 5 4 3 2  1  0\n");
   printf("----------------------\n");
   printf("Queue:  ");
	
   while(!isEmpty()){
      int n = removeData();           
      printf("%d ",n);
   }   
}

如果我們編譯並執行上述程式，那麼這將產生以下結果 -

Queue is full!
Element removed: 1
Element at front: 3
----------------------
index : 5 4 3 2 1 0
----------------------
Queue: 3 5 9 12 15 16