圖資料結構

圖是一個集合，其中一些對物件都是通過鏈路連線的物件的圖形表示。互聯的物件是通過頂點來表示，以及連線所述頂點的連結被稱為邊緣。

形式上，曲線圖是一對集(V, E), 其中V是頂點組及E是邊集，連線頂點的對。看看下面的圖 -

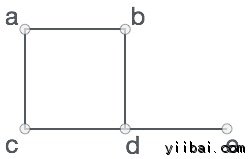
另外，在上述圖中，

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

圖資料結構

數學圖可在資料結構中表示。我們可以使用頂點陣列和邊緣的二維陣列來表示圖。 在進一步前進學習前，讓我們熟悉一下一些重要術語?

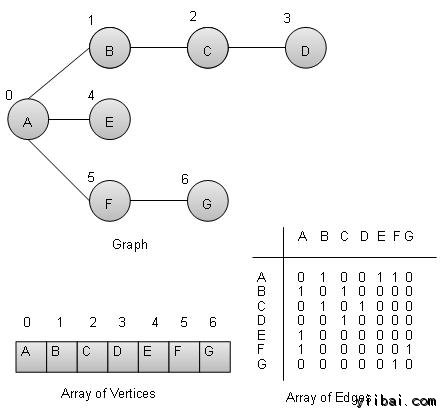
• 頂點 ? 圖的每個節點被表示為頂點。在下面的例子中給出，標記圓圈代表頂點。因此，A至G的頂點。使用陣列，如下面的圖片我們可以代表他們。這裡A可以通過索引0，B可以使用索引1等來識別。

• 邊緣 ? 邊表示兩個頂點之間的線的兩個頂點之間的路徑。在下面的例子中給出，線路從A到B，B到C等代表邊緣。我們可以用一個二維陣列來表示陣列所示圖如下。這裡AB可以表示為1，在第0行，第1列，BC為1，在第1行，列2等等，保持其他的組合為0。

• 相鄰 ? 兩個節點或頂點相鄰當它們通過一個邊彼此連線。在下面的例子給出，B是相鄰的A，C是相鄰B等。

• 通路 ? 路徑代表兩個頂點之間的邊的序列。在下面的例子給出ABCD表示從A到D的路徑。

基本操作

以下是遵循圖的基本操作。

• 新增頂點 ? 新增一個頂點到圖。

• 新增邊緣 ? 圖的兩個頂點之間新增邊線。

• 顯示頂點 ? 顯示一個圖形的頂點。

新增頂點操作

//add vertex to the vertex list
void addVertex(char label){
   struct vertex* vertex = (struct vertex*) malloc(sizeof(struct vertex));
   vertex->label = label;  
   vertex->visited = false;     
   lstVertices[vertexCount++] = vertex;
}

新增邊緣操作

//add edge to edge array
void addEdge(int start,int end){
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}

顯示邊緣操作

//display the vertex
void displayVertex(int vertexIndex){
   printf("%c ",lstVertices[vertexIndex]->label);
}