TensorFlow數學基礎

在TensorFlow中建立基本應用程式之前，了解TensorFlow所需的數學概念非常重要。數學是任何機器學習演算法的核心。在數學核心概念的幫助下，定義了特定機器學習演算法的解決方案。

向量

將數位陣列(連續或離散)定義為向量。機器學習演算法處理固定長度向量以產生更好的輸出。

機器學習演算法處理多維資料，因此向量起著至關重要的作用。

向量模型的圖形表示如下所示 -

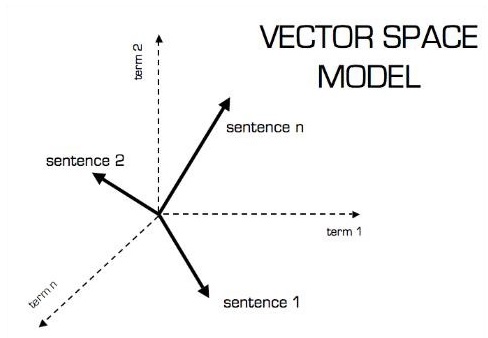
標量

標量可以定義為一維向量。標量是那些僅包括大小而沒有方向的標量。對於標量，我們只關注幅度。

標量的範例：兒童的體重和身高引數。

矩陣

矩陣可以定義為多維陣列，以行和列的格式排列。矩陣的大小由行長度和列長度定義。下圖顯示了任何指定矩陣的表示。

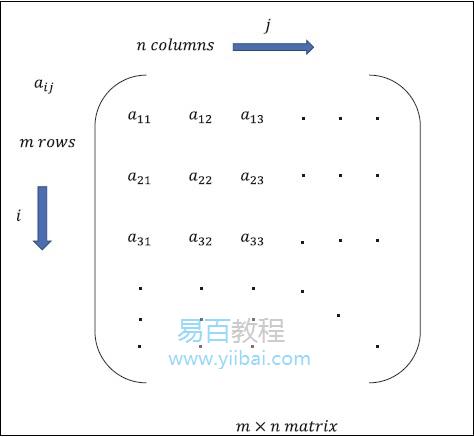
考慮如上所述的具有「m」行和「n」列的矩陣，矩陣表示將指定為「m * n矩陣」，其也定義了矩陣的長度。

數學計算

在本節中，我們將了解TensorFlow中的數學計算。

矩陣相加
如果矩陣具有相同的尺寸，則可以相加兩個或更多個矩陣。相加表示根據給定位置新增每個元素。

請考慮以下範例以了解矩陣的相加方式是如何工作的 -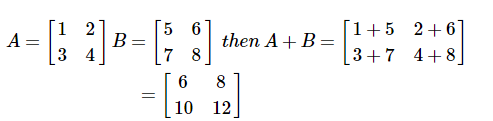

矩陣減法
矩陣的減法以類似於新增兩個矩陣的方式操作。如果尺寸相等，使用者可以減去兩個矩陣。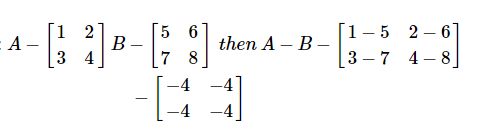

矩陣乘法
對於兩個矩陣A m * n和B p * q是可乘的，n應該等於p。得到的矩陣是 -

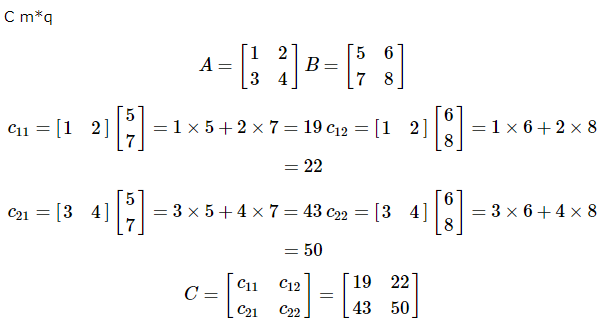
矩陣的轉置
矩陣A，m * n的轉置通常由AT(轉置)n * m表示，並且通過將列向量轉置為行向量而獲得。

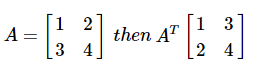
向量的點積
尺寸n的任何向量可以表示為矩陣v = R ^ n * 1。

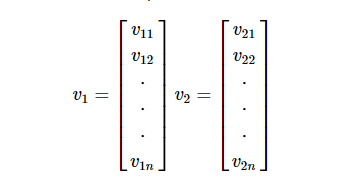
兩個向量的點積是相應元件的乘積之和 - 沿相同維度的元件，可以表示為：

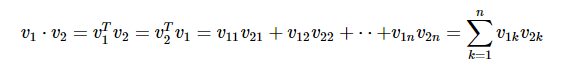
向量點積的例子如下 -