Scipy ODR

ODR代表正交距離回歸，用於回歸研究。 基本線性回歸通常用於通過在圖上繪製最佳擬合線來估計兩個變數y和x之間的關係。

用於此的數學方法稱為最小平方，旨在最小化每個點的平方誤差總和。 這裡的關鍵問題是如何計算每個點的誤差(也稱為殘差)？

在一個標準的線性回歸中，目的是從X值預測Y值 - 因此明智的做法是計算Y值的誤差(如下圖所示的灰線所示)。 但是，有時考慮X和Y的誤差(如下圖中的紅色虛線所示)更為明智。

例如 - 當知道對X的測量是不確定的，或者當不想關注一個變數相對於另一個變數的錯誤時。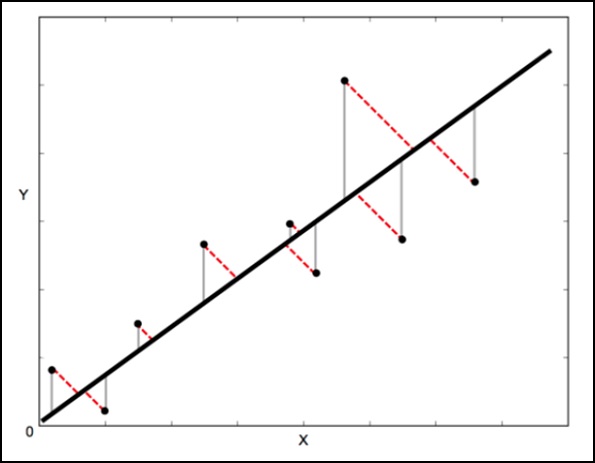

正交距離回歸(ODR)是一種可以做到這一點的方法(正交在這裡表示為垂直 - 所以它計算垂直於線的誤差，而不僅僅是’垂直’)。

單變數回歸的scipy.odr實現

以下範例演示單變數回歸的scipy.odr實現。

import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random

# Initiate some data, giving some randomness using random.random().
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i**2 + random.random() for i in x])

# Define a function (quadratic in our case) to fit the data with.
def linear_func(p, x):
   m, c = p
   return m*x + c

# Create a model for fitting.
linear_model = Model(linear_func)

# Create a RealData object using our initiated data from above.
data = RealData(x, y)

# Set up ODR with the model and data.
odr = ODR(data, linear_model, beta0=[0., 1.])

# Run the regression.
out = odr.run()

# Use the in-built pprint method to give us results.
out.pprint()

上述程式將生成以下輸出 -

Beta: [ 5.50355382 -3.88825011]
Beta Std Error: [ 0.77904626  2.33231797]
Beta Covariance: [[  1.92223609  -4.80559051]
 [ -4.80559051  17.22882877]]
Residual Variance: 0.31573284521355344
Inverse Condition #: 0.1465848083469268
Reason(s) for Halting:
  Sum of squares convergence