Scipy積分
當一個函式不能被分析積分,或者很難分析積分時,通常會轉向數值積分方法。 SciPy有許多用於執行數值積分的程式。 它們中的大多數都在同一個scipy.integrate庫中。 下表列出了一些常用函式。
| 編號 | 範例 | 描述 |
|---|---|---|
| 1 | quad |
單積分 |
| 2 | dblquad |
二重積分 |
| 3 | tplquad |
三重積分 |
| 4 | nquad |
n倍多重積分 |
| 5 | fixed_quad |
高斯積分,階數n |
| 6 | quadrature |
高斯正交到容差 |
| 7 | romberg |
Romberg積分 |
| 8 | trapz |
梯形規則 |
| 9 | cumtrapz |
梯形法則累計計算積分 |
| 10 | simps |
辛普森的規則 |
| 11 | romb |
Romberg積分 |
| 12 | polyint |
分析多項式積分(NumPy) |
| 13 | poly1d |
輔助函式polyint(NumPy) |
單積分
Quad函式是SciPy積分函式的主力。 數值積分有時稱為正交積分,因此稱為名稱。 它通常是在a到b給定的固定範圍內執行函式f(x)的單個積分的預設選擇。
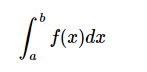
quad的一般形式是scipy.integrate.quad(f,a,b),其中'f'是要積分的函式的名稱。 而'a'和'b'分別是下限和上限。 下面來看看一個高斯函式的例子,它的積分範圍是0和1。
首先需要定義這個函式: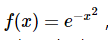
這可以使用lambda表示式完成,然後在該函式上呼叫四方法。
import scipy.integrate
from numpy import exp
f= lambda x:exp(-x**2)
i = scipy.integrate.quad(f, 0, 1)
print (i)
執行上面範例程式碼,得到以下結果 -
(0.7468241328124271, 8.291413475940725e-15)
四元函式返回兩個值,其中第一個數位是積分值,第二個數值是積分值絕對誤差的估計值。
註 - 由於
quad需要函式作為第一個引數,因此不能直接將exp作為引數傳遞。 Quad函式接受正和負無窮作為限制。 Quad函式可以積分單個變數的標準預定義NumPy函式,如exp,sin和cos。
多重積分
雙重和三重積分的機制已被包含到函式dblquad,tplquad和nquad中。 這些函式分別積分了四個或六個引數。 所有內積分的界限都需要定義為函式。
雙重積分
dblquad的一般形式是scipy.integrate.dblquad(func,a,b,gfun,hfun)。 其中,func是要積分函式的名稱,'a'和'b'分別是x變數的下限和上限,而gfun和hfun是定義變數y的下限和上限的函式名稱。
看看一個執行雙重積分方法的範例。
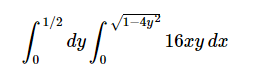
使用lambda表示式定義函式f,g和h。 請注意,即使g和h是常數,它們可能在很多情況下必須定義為函式,正如在這裡為下限所做的那樣。
import scipy.integrate
from numpy import exp
from math import sqrt
f = lambda x, y : 16*x*y
g = lambda x : 0
h = lambda y : sqrt(1-4*y**2)
i = scipy.integrate.dblquad(f, 0, 0.5, g, h)
print (i)
執行上面範例程式碼,得到以下結果 -
(0.5, 1.7092350012594845e-14)
除上述例程外,scipy.integrate還有許多其他積分的程式,其中包括執行n次多重積分的nquad以及實現各種整合演算法的其他例程。 但是,quad和dblquad將滿足對數值積分的大部分需求。