Matlab轉換

MATLAB提供了處理轉換的命令，如拉普拉斯和傅里葉變換。轉換在科學和工程中被用作簡化分析和從另一個角度看待資料的工具。

例如，傅里葉(Fourier)轉換允許我們將表示為時間的函式的信號轉換為頻率的函式。 拉普拉斯變換允許我們將微分方程轉換為代數方程。

MATLAB提供了laplace，fourier和fft命令來處理拉普拉斯，傅立葉和快速傅里葉轉換。

拉普拉斯變換

時間f(t)函式的拉普拉斯轉換由以下積分 -

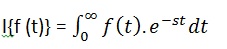
拉普拉斯變換也表示為f(t)到F(s)的變換。 可以看到此變換或整合過程將f(t)，符號變數t的函式轉換為另一個函式F(s)與另一個變數s。

拉普拉斯變換將微分方程轉換為代數方程。要計算函式f(t)的拉普拉斯變換，參考以下程式碼 -

laplace(f(t))

範例

在這個例子中，我們將計算一些常用函式的拉普拉斯變換。

建立指令碼檔案並鍵入以下程式碼 -

syms s t a b w
laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))

MATLAB執行檔案程式碼時，得到以下結果 -

Trial>> syms s t a b w
laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))

ans =

1/s^2


ans =

2/s^3


ans =

362880/s^10


ans =

1/(b + s)


ans =

w/(s^2 + w^2)


ans =

s/(s^2 + w^2)

逆拉普拉斯變換

MATLAB中可使用命令ilaplace來計算逆拉普拉斯變換。

例如，

ilaplace(1/s^3)

MATLAB執行上述程式碼語句得到以下結果 -

ans =
 t^2/2

範例
建立指令碼檔案並鍵入以下程式碼 -

syms s t a b w
ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))

MATLAB執行上述程式碼語句得到以下結果 -

ans =
t^6/720

 ans =
 2*exp(-t*w)

 ans =
 cos(2*t)

 ans =
 ilaplace(exp(-b*t), t, x)

 ans =
 sin(t*w)

 ans =
 cos(t*w)

傅里葉變換

傅里葉變換通常將時間f(t)的數學函式轉換成有時由F表示的新函式，其引數是以周期/ s(赫茲)或每秒弧度為單位的頻率。新功能被稱為傅立葉變換和/或函式f的頻譜。

範例

建立指令碼檔案並在其中鍵入以下程式碼 -

syms x 
f = exp(-2*x^2);  %our function
ezplot(f,[-2,2])  % plot of our function
FT = fourier(f)    % Fourier transform

MATLAB執行上述程式碼語句得到以下結果 -

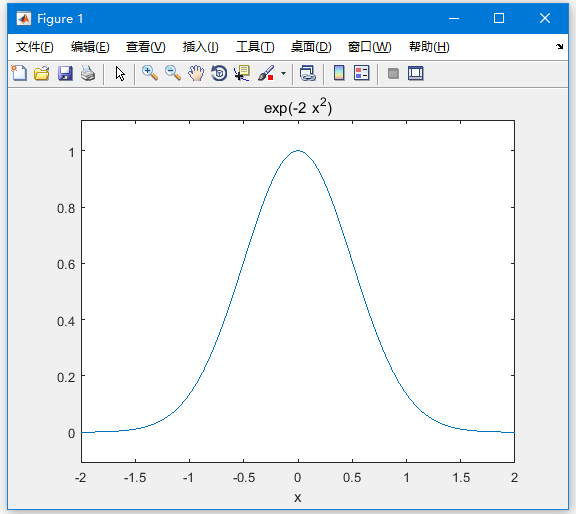
同時也會輸出以下結果 -

Trial>> syms x 
f = exp(-2*x^2);  %our function
ezplot(f,[-2,2])  % plot of our function
FT = fourier(f)    % Fourier transform

FT =

(2^(1/2)*pi^(1/2)*exp(-w^2/8))/2

繪製傅里葉變換為 -

syms x 
f = exp(-2*x^2);  %our function
% ezplot(f,[-2,2])  % plot of our function
FT = fourier(f)    % Fourier transform
ezplot(FT)

MATLAB執行上述程式碼語句得到以下結果 -

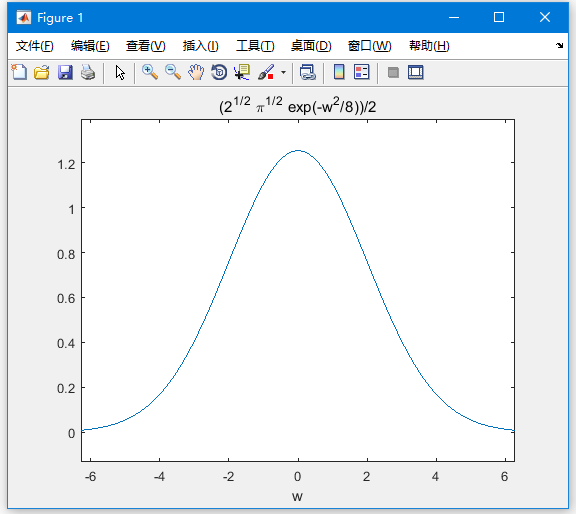
逆傅里葉變換

MATLAB提供了用於計算函式的逆傅里葉變換的ifourier命令。 例如，

f = ifourier(-2*exp(-abs(w)))

MATLAB將執行上述語句並顯示結果 -

f =
-2/(pi*(x^2 + 1))