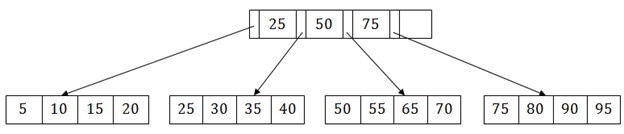
DBMS B+樹

B+樹 是一個平衡的二元搜尋樹，它遵循多級索引格式。

• 在B+樹中，葉節點表示實際的資料指標，B+樹確保所有葉節點保持在相同的高度。
• 在B+樹中，葉節點使用連結串列連結，因此，B+樹可以支援隨機存取以及順序存取。

B+樹的結構

在B+樹中，每個葉節點與根節點的距離相等。B+樹的順序為n，其中n對於每個B+樹是固定的。
它包含內部節點和葉節點。

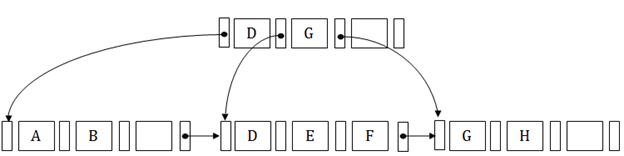
內部節點

• B+樹的內部節點可以包含除根節點之外的至少 n/2 個記錄指標。
• 最多，樹的內部節點包含n 個指標。

葉節點

• B+樹的葉節點可以包含至少n/2 個記錄指標和n/2個鍵值。
• 葉節點最多包含n個記錄指標和n個鍵值。
• B+樹的每個葉節點包含一個塊指標P以指向下一個葉節點。

在B+樹中搜尋記錄

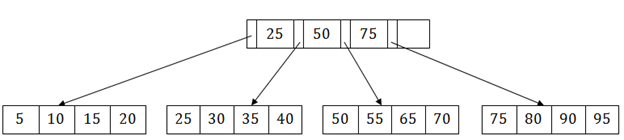
假設要在下面的B+樹結構中搜尋55。 首先，獲取中間節點，該節點將指向可包含55的記錄的葉節點。

因此，在中間節點中，將找到50到75個節點之間的分支。 然後在最後，重定向到第三個葉節點。這裡DBMS將執行順序搜尋以找到55。

B+樹插入

假設要在下面的結構中插入記錄60。 它將在55之後轉到第3個葉子節點。它是一個平衡樹，並且該樹的葉節點已經滿了，所以不能在那裡插入60。

在這種情況下，必須要拆分葉節點，以便可以將其插入樹中而不會影響填充因子，平衡和順序。

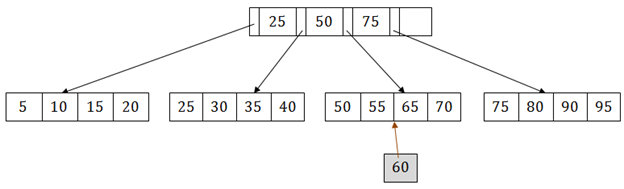
第3個葉節點具有值(50,55,60,65,70)，其當前根節點為50。在中間拆分樹的葉節點，以便不改變其平衡。 因此，可以將(50,55)和(60,65,70)分組為2個葉節點。

這兩個必須是葉節點，則中間節點不能從50分支。它應該新增60，然後有一個指向新葉節點的指標。

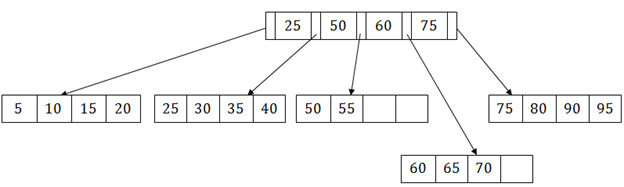
這是在有溢位時插入條目的方法。 在正常情況下，很容易找到它所適合的節點，然後將其放在該葉節點中。

B+樹刪除

假設要從上面的例子中刪除60。 在這種情況下需要從中間節點以及第4葉節點中刪除60。 如果從中間節點中刪除它，那麼樹將不滿足B+樹的規則。 所以需要修改它以獲得平衡的樹。

從B+樹上方刪除節點60並重新排列節點後，將顯示如下：