開啟可變或嚴格的交替方式

Turn Variable或Strict Alternation Approach是在使用者模式下實現的軟體機制。 這是一個繁忙的等待解決方案，只能為兩個進程實施。 在這種方法中，使用實際上是鎖的轉彎變數。

這種方法只能用於兩個進程。 一般來說，讓兩個進程是:Pi和Pj。 它們共用一個稱為轉變數的變數。 程式的虛擬碼可以給出如下。

對於進程Pi

Non - CS   
while (turn ! = i);   
Critical Section   
turn = j;   
Non - CS

對於進程Pj

Non - CS   
while (turn ! = j);  
Critical Section   
turn = i ;  
Non - CS

鎖變數方法的實際問題是只有當鎖變數為1時進程才進入臨界區。不止一個進程可以同時看到鎖變數為1，因此互斥不能得到保證。

這個問題在轉向變數方法中得到解決。 現在，只有當轉向變數的值等於進程的PID時，進程才能進入臨界區。

只有兩個可能的值是可變的，i或j。 如果它的值不是i，那麼肯定會是j，反之亦然。

在入口部分，一般來說，進程Pi不會進入臨界區，直到它的值為j，或者進程Pj將不會進入臨界區，直到其值為i。

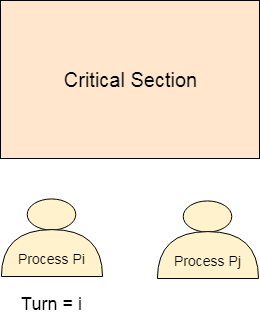
最初，兩個進程Pi和Pj可用並且想要執行到臨界區。

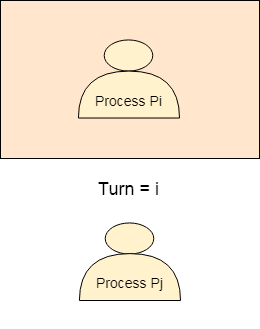
轉向變數等於i，因此Pi將有機會進入臨界區。 在Pi完成臨界區之前，Pi的值仍然為I。

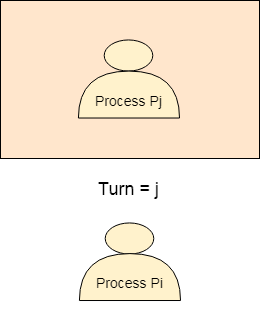
Pi完成其臨界區並指定j轉變。 Pj將有機會進入臨界區。 轉變值仍然是j直到Pj完成其臨界區。

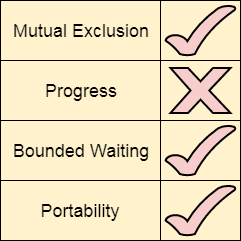
嚴格交替法分析

讓我們根據四個要求分析嚴格交替方法。

相互排斥
嚴格的交替方法在每種情況下都提供相互排斥。 此過程僅適用於兩個進程。 這兩個進程的虛擬碼是不同的。 只有在看到轉彎變數等於其過程ID時才會進入該過程，否則不會進入。因此，無論進程如何，進程都不能進入臨界區。

進程

這一機制無法保證進展。 如果Pi不想進入臨界區，那麼Pj被無限期阻擋。 Pj必須等待很長時間，因為轉向變數將保持為0，直到Pi將其分配給j。

可移植性
該解決方案提供了便攜性。 它是在使用者模式下實現的純粹的軟體機制，不需要作業系統的任何特殊指令。