人工智慧的最小最大演算法
人工智慧中的最小最大演算法:
- Mini-max演算法是一種遞回或回溯演算法,用於決策和博弈論。它為玩家提供了一個最佳的動作,假設對手也在玩最佳狀態。
- Mini-Max演算法使用遞回來搜尋遊戲樹。
- Min-Max演算法主要用於AI中的遊戲。如Chess,Checkers,tic-tac-toe,go和各種拖車玩家遊戲。該演算法計算當前狀態的最小極大決策。
- 在該演算法中,兩個玩家玩遊戲,一個叫做MAX,另一個叫做MIN。
- 當對手玩家獲得最大利益時,兩個玩家都會對抗它。
- 遊戲的兩個玩家都是彼此的對手,其中MAX將選擇最大化值,MIN將選擇最小化值。
- minimax演算法執行深度優先搜尋演算法以探索完整的遊戲樹。
- minimax演算法一直向下到樹的終端節點,然後作為遞回回溯樹。
MiniMax演算法的虛擬碼:
function minimax(node, depth, maximizingPlayer) is
if depth ==0 or node is a terminal node then
return static evaluation of node
if MaximizingPlayer then // for Maximizer Player
maxEva= -infinity
for each child of node do
eva= minimax(child, depth-1, false)
maxEva= max(maxEva,eva) //gives Maximum of the values
return maxEva
else // for Minimizer player
minEva= +infinity
for each child of node do
eva= minimax(child, depth-1, true)
minEva= min(minEva, eva) //gives minimum of the values
return minEva
初始呼叫:
Minimax(node, 3, true)
Min-Max演算法的工作
- 使用範例可以容易地描述minimax演算法的工作。下面舉一個代表雙人遊戲的遊戲樹的例子。
- 在這個例子中,有兩個玩家,一個叫做Maximizer,另一個叫做Minimizer。
- Maximizer將嘗試獲得最大可能分數,而Minimizer將嘗試獲得最低分數。
- 這個演算法適用於DFS,因此在這個遊戲樹中,必須一直通過葉子到達終端節點。
- 在終端節點處,給出終端值,因此將比較這些值並回溯樹,直到初始狀態發生。以下是解決雙人遊戲樹所涉及的主要步驟:
第1步: 在第一步中,演算法生成整個遊戲樹並應用效用函式來獲取終端狀態的效用值。在下面的樹形圖中,下面來看看A是樹的初始狀態。假設Maximizer採用具有最壞情況初始值 = -無窮大的第一次轉彎,並且Minimizer將採用具有最壞情況初始值=+無窮大的下一轉彎。
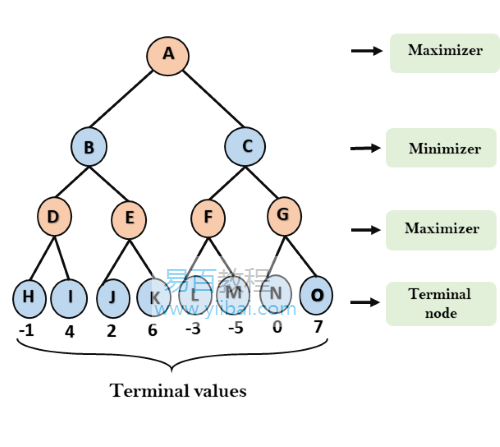
第2步:現在,首先我們找到Maximizer的效用值,它的初始值是-∞,因此將比較終端狀態中的每個值和Maximizer的初始值,並確定更高的節點值。它將在所有人中找到最大值。
- 對於節點 D max(-1,- -∞) => max(-1,4)= 4
- 對於節點 E max(2, -∞) => max(2, 6)= 6
- 對於節點 F max(-3, -∞) => max(-3,-5) = -3
- 對於節點 G max(0, -∞) = max(0, 7) = 7
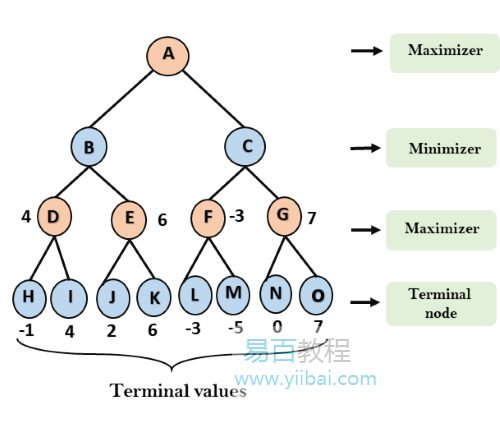
第3步:現在輪到Maximizer,它將再次選擇所有節點的最大值並找到根節點的最大值。在這個遊戲樹中,只有4層,因此我們立即到達根節點,但在真實遊戲中,將有超過4層。
- 對於節點A ,max(4, -3)= 4
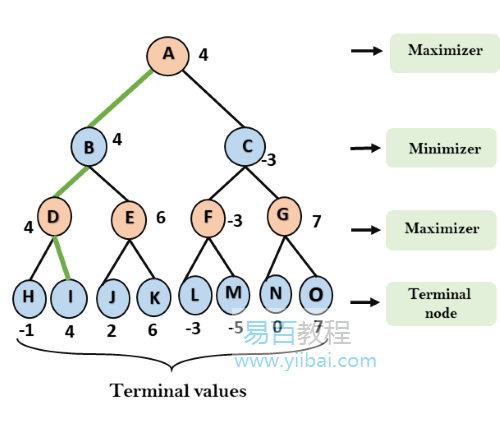
上面就是minimax雙人遊戲的完整工作流程。
Mini-Max演算法的屬性
- Complete-Min-Max演算法是完整的。它肯定會在有限搜尋樹中找到解決方案(如果存在)。
- 如果兩個對手都以最佳方式進行遊戲,則Optimal-Min-Max演算法是最佳的。
- 時間複雜度 - 當它為遊戲樹執行DFS時,Min-Max演算法的時間複雜度為O(b^m),其中b是遊戲樹的分支因子,m是樹的最大深度。
- 空間複雜度 - Mini-max演算法的空間複雜度也類似於DFS,即O(bm)。
極小極大演算法的侷限性
- minimax演算法的主要缺點是它物件棋,go等複雜遊戲來說非常慢。這種型別的遊戲有很大的分支因素,玩家有很多選擇可以決定。minimax演算法的這種限制可以通過我們在下一個主題中討論的alpha-beta修剪來改進。