人工智慧爬山演算法

爬山(Hill Climbing)演算法是一種區域性搜尋演算法，它在增加高度/值的方向上連續移動，以找到山峰或最佳解決問題的方法。它在達到峰值時終止，其中沒有鄰居具有更高的值。
爬山演算法是一種用於優化數學問題的技術。其中一個廣泛討論的爬山演算法的例子是旅行商問題，其中我們需要最小化推銷員的行進距離。
它也稱為貪婪的本地搜尋，因為它只關注其良好的直接鄰居狀態而不是超越它。爬山演算法的節點有兩個組成部分，即狀態和值。
Hill Climbing主要用於有良好啟發式的時候。在此演算法中，不需要維護和處理搜尋樹或圖形，因為它只保留單個當前狀態。

爬山演算法的特點

以下是爬山演算法的一些主要特徵：

• 生成和測試變體：Hill Climbing是Generate和Test方法的變體。生成和測試方法產生反饋，有助於確定在搜尋空間中移動的方向。
• 貪婪的方法：爬山演算法搜尋朝著優化成本的方向發展。
• 沒有回溯：它不會回溯蒐尋空間，因為它不記得以前的狀態。

爬山的國家空間圖

狀態空間景觀是爬山演算法的圖形表示，其示出了演算法的各種狀態和目標函式/成本之間的圖。

在Y軸上，我們採用了可以是目標函式或成本函式的函式，以及x軸上的狀態空間。如果Y軸上的函式是成本，那麼搜尋的目標是找到全域性最小值和區域性最小值。如果Y軸的函式是目標函式，那麼搜尋的目標是找到全域性最大值和區域性最大值。

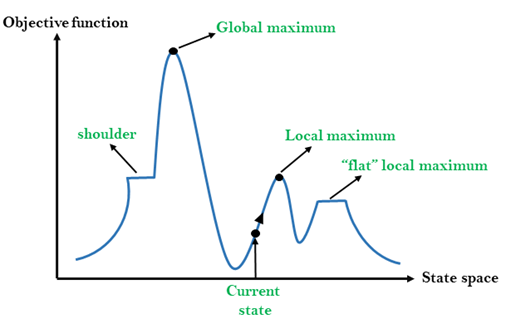
狀態的不同區域

區域性最大值：區域性最大值是一個比其鄰居狀態更好的狀態，但也有另一個高於它的狀態。
全域性最大值：全域性最大值是狀態空間最佳狀態。它具有最高的目標函式值。
當前狀態：它是當前存在代理的橫向圖中的狀態。
平局區域性最大值：它是景觀中的平坦空間，其中當前狀態的所有鄰居狀態具有相同的值。
肩部：這是一個具有上坡邊緣的高原地區。

爬山型別演算法：

• 簡單爬山
• Steepest-Ascent爬山
• 隨機爬山

1 簡單爬山

簡單的爬山是實現爬山演算法的最簡單方法。它一次只評估鄰居節點狀態，並選擇第一個優化當前成本並將其設定為當前狀態的狀態。它只檢查它的一個後繼狀態，如果它發現優於當前狀態，則移動其他狀態。該演算法具有以下特徵：

• 減少耗時
• 不太保證不太理想的解決方案和解決方案

簡易爬山演算法：

• 步驟1：評估初始狀態，如果是目標狀態，則返回成功並停止。
• 步驟1：迴圈直到找到解決方案或沒有新的運算子可供應用。
• 步驟3：選擇並將運算子應用於當前狀態。

• 步驟4：檢查新狀態：

  • 如果是目標狀態，則返回成功並退出。
  • 否則，如果它優於當前狀態，則將新狀態指定為當前狀態。
  • 否則如果不比當前狀態好，則返回步驟2。
• 步驟5：退出

Steepest-Ascent爬坡：

最陡峭的Ascent演算法是簡單爬山演算法的變體。該演算法檢查當前狀態的所有相鄰節點，並選擇最接近目標狀態的一個鄰居節點。該演算法在搜尋多個鄰居時會消耗更多時間

最速爬坡爬山演算法：

• 步驟1：評估初始狀態，如果是目標狀態，則返回成功並停止，否則將當前狀態作為初始狀態。
• 步驟2：迴圈直到找到解決方案或當前狀態不變。
  • 讓SUCC成為一個狀態，使得當前狀態的任何繼承者都會比它更好。
  • 對於適用於當前狀態的每個運算子：
    • 應用new運算子並生成新狀態。
    • 評估新的狀態。
    • 如果是目標狀態，則返回並退出，否則將其與SUCC進行比較。
    • 如果它優於SUCC，則將新狀態設定為SUCC。
    • 如果SUCC優於當前狀態，則將當前狀態設定為SUCC。
• 步驟3：退出

隨機爬山：

隨機爬山在移動之前不會檢查其所有鄰居。相反，該搜尋演算法隨機選擇一個鄰居節點並決定是將其選擇為當前狀態還是檢查另一個狀態。

爬山演算法存在的問題

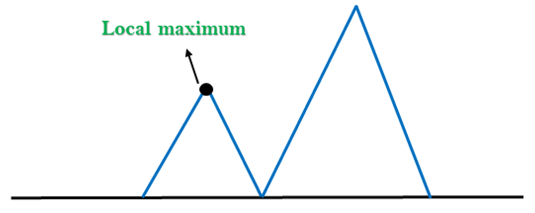
1. 區域性最大值：區域性最大值是景觀中的峰值狀態，其優於每個相鄰狀態，但是還存在另一個高於區域性最大值的狀態。

解決方案：回溯技術可以解決狀態空間景觀中的區域性最大值。建立有前途的路徑列表，以便演算法可以回溯蒐尋空間並探索其他路徑。

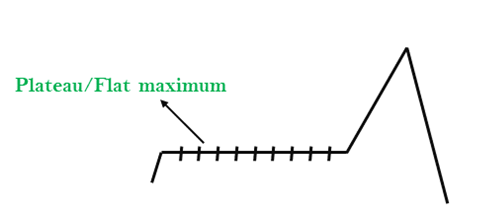
2.高原：高原是搜尋空間的平坦區域，其中當前狀態的所有鄰居狀態包含相同的值，因為該演算法沒有找到任何最佳移動方向。在高原地區可能會失去爬山搜尋。

解決方案：高原的解決方案是在搜尋時採取大步驟或非常小的步驟來解決問題。隨機選擇遠離當前狀態的狀態，因此演算法可能找到非平穩區域。

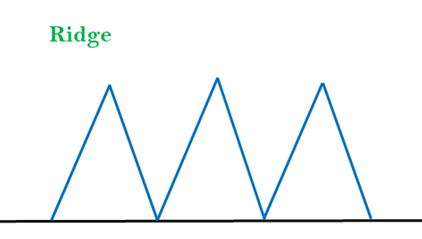
3.山脊：山脊是區域性最大值的特殊形式。它的面積高於周圍區域，但本身有一個斜坡，一次搬不到。

解決方案：通過使用雙向搜尋或向不同方向移動，可以改善此問題。

模擬退火

爬山演算法從不會向較低的值移動，因此可以保持不完整，因為它可能會卡在區域性最大值上。如果演算法應用隨機游走，通過移動後繼，那麼它可能完成但效率不高。模擬退火是一種既能提高效率又能實現完整性的演算法。

在機械術語中，退火是將金屬或玻璃硬化至高溫然後逐漸冷卻的過程，因此這允許金屬達到低能晶態。在模擬退火中使用相同的過程，其中演算法選擇隨機移動，而不是選擇最佳移動。如果隨機移動改善了狀態，則它遵循相同的路徑。否則，演算法遵循概率小於1的路徑或者下坡移動並選擇另一條路徑。