知情搜尋演算法

在前面章節中，我們已經討論了不知情搜尋演算法，該搜尋演算法通過搜尋空間查詢問題的所有可能解決方案，而無需任何關於搜尋空間的額外知識。但是，知情搜尋(Informed Search)演算法包含一系列知識，例如我們離目標有多遠，路徑成本，如何到達目標節點等。這些知識有助於代理人更少地探索搜尋空間並更有效地找到目標節點。

知情搜尋演算法對於大型搜尋空間更有用。知情搜尋演算法使用啟發式思想，因此也稱為啟發式搜尋。

啟發式函式：啟發式是一種在Informed Search中使用的函式，它找到了最有希望的路徑。它將代理的當前狀態作為其輸入，並生成估計代理與目標的接近程度。然而，啟發式方法可能並不總是提供最佳解決方案，但它保証在合理的時間內找到一個好的解決方案。啟發式函式估計狀態與目標的接近程度。它由h(n)表示，它計算這對狀態之間的最佳路徑的成本。啟發式函式的值始終為正值。

啟發函式的可接受性如下：

h(n) <= h*(n)

這裡h(n)是啟發式成本，h *(n)是估計成本。因此，啟發式成本應小於或等於估計成本。

純啟發式搜尋

純啟發式搜尋是最簡單的啟發式搜尋演算法。它根據啟發式值h(n)擴充套件節點。它維護兩個列表，OPEN和CLOSED列表。在CLOSED列表中，它放置那些已經擴充套件的節點，並在OPEN列表中放置尚未展開的節點。

在每次疊代中，具有最低啟發式值的每個節點n被擴充套件並生成其所有後繼者，並且n被放置到閉合列表中。該演算法繼續單元找到目標狀態。

在知情搜尋中，我們將討論以下兩種主要演算法：

• 最佳搜尋演算法(貪婪搜尋)
• A *搜尋演算法

1. 最佳搜尋演算法(貪婪搜尋)

貪心最佳優先搜尋演算法總是選擇當時最佳的路徑。它是深度優先搜尋和廣度優先搜尋演算法的組合。它使用啟發式功能和搜尋。最佳優先搜尋允許我們利用這兩種演算法的優勢。借助最佳優先搜尋，在每一步，我們都可以選擇最有前途的節點。在最好的第一搜尋演算法中，我們擴充套件最接近目標節點的節點，並且通過啟發函式估計最接近的成本，即 -

f(n)= g(n)

是，h(n)= 從節點n到目標的估計成本。

貪婪最佳優先演算法由優先順序佇列實現。

最佳優先搜尋演算法：

• 步驟1：將起始節點放入OPEN列表。
• 步驟2：如果OPEN列表為空，則停止並返回失敗。
• 步驟3：從具有最低值h(n)的OPEN列表中刪除節點n，並將其放在CLOSED列表中。
• 步驟4：展開節點n，並生成節點n的後繼節點。
• 步驟5：檢查節點n的每個後繼節點，並查詢是否有任何節點是目標節點。如果任何後繼節點是目標節點，則返回成功並終止搜尋，否則繼續執行步驟6。
• 步驟6：對於每個後繼節點，演算法檢查評估函式f(n)，然後檢查節點是否已處於OPEN或CLOSED列表中。如果節點未在兩個列表中，則將其新增到OPEN列表中。
• 步驟7：返回步驟2。

優點：

• 最佳優先搜尋可以通過獲得兩種演算法的優勢在BFS和DFS之間切換。
• 該演算法比BFS和DFS演算法更有效。

缺點：

• 在最壞的情況下，它可以表現為無指導的深度優先搜尋。
• 它可以像DFS一樣陷入迴圈。
• 該演算法不是最優的。

範例：

考慮下面的搜尋問題，我們將使用貪婪的最佳優先搜尋來遍歷它。在每次疊代時，使用評估函式f(n)= h(n)擴充套件每個節點，該函式在下表中給出。

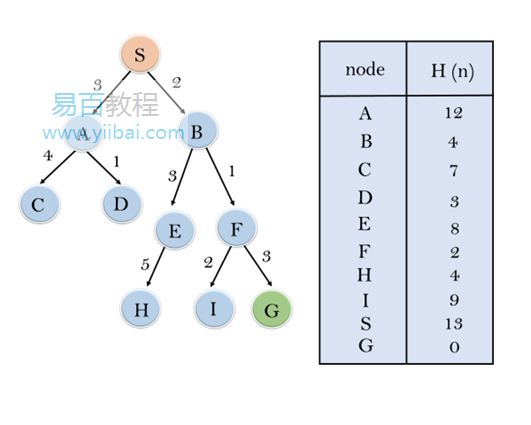
在此搜尋範例中，我們使用兩個列表，即OPEN和CLOSED列表。以下是遍歷上述範例的疊代。

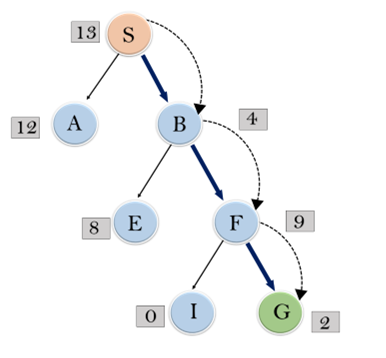
展開S的節點並放入CLOSED列表

初始:

Open [A, B], Closed [S]

疊代 1:

Open [A], Closed [S, B]

疊代 2:

Open [E, F, A], Closed [S, B]
                  : Open [E, A], Closed [S, B, F]

疊代 3:

Open [I, G, E, A], Closed [S, B, F]
                  : Open [I, E, A], Closed [S, B, F, G]

因此最終的解決方案路徑為：S ——> B ——-> F ——> G.

時間複雜性：最佳優先搜尋的最壞情況時間複雜度是O(bm)。
空間複雜性：最佳優先搜尋的最壞情況空間複雜度是O(bm)。其中，m是搜尋空間的最大深度。
完成：即使給定的狀態空間是有限的，貪婪最佳優先搜尋也是不完整的。
最優：貪心最佳優先搜尋演算法不是最優的。

2. A *搜尋演算法：

A *搜尋是最常見的最佳優先搜尋形式。它使用啟發函式h(n)，並且從開始狀態g(n)到達節點n的成本。它結合了UCS和貪婪的最佳優先搜尋功能，可以有效地解決問題。A *搜尋演算法使用啟發式函式找到通過搜尋空間的最短路徑。此搜尋演算法擴充套件了較少的搜尋樹並更快地提供最佳結果。A *演算法類似於UCS，除了它使用g(n)+ h(n)而不是g(n)。

在A *搜尋演算法中，我們使用搜尋啟發式以及到達節點的成本。因此可以將兩種成本結合起來，並將此總和稱為適合度數。

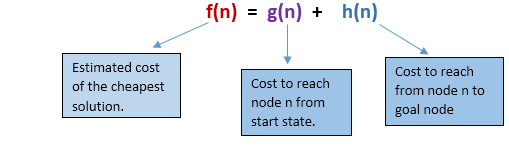
在搜尋空間中的每個點處，僅擴充套件具有最小值f(n)的那些節點，並且演算法在找到目標節點時終止。

A *搜尋演算法過程

• 步驟1：將起始節點放在OPEN列表中。
• 步驟2：檢查OPEN列表是否為空，如果列表為空則返回失敗並停止。
• 步驟3：從OPEN列表中選擇具有最小評估函式值(g + h)的節點，如果節點n是目標節點則返回成功並停止，否則繼續。
• 步驟4：展開節點n並生成其所有後繼節點，並將n放入關閉列表中。對於每個後來者n’，檢查n’是否已經在OPEN或CLOSED列表中，如果沒有，則檢查n’的評估函式並放入開啟列表。
• 步驟5：否則如果節點n’已經處於OPEN和CLOSED狀態，那麼它應該連線到反向最低g(n’)值的後向指標。
• 步驟6：返回步驟2。

優點：

• A * 搜尋演算法是比其他搜尋演算法更好的演算法。
• A * 搜尋演算法是最佳和完整的。
• 該演算法可以解決非常複雜的問題。

缺點：

• 它並不總是產生最短路徑，因為它主要基於啟發式和近似。
• A * 搜尋演算法存在一些複雜性問題。
• A * 主要缺點是記憶體需求，因為它將所有生成的節點儲存在記憶體中，因此對於各種大規模問題是不實際的。

範例：

在這個例子中，我們將使用A * 演算法遍歷給定的圖形。所有狀態的啟發式值在下表中給出，因此將使用公式f(n)= g(n)+ h(n)計算每個狀態的f(n)，其中g(n)是成本 從開始狀態到達任何節點。
下面是將使用OPEN和CLOSED列表。

解決方案

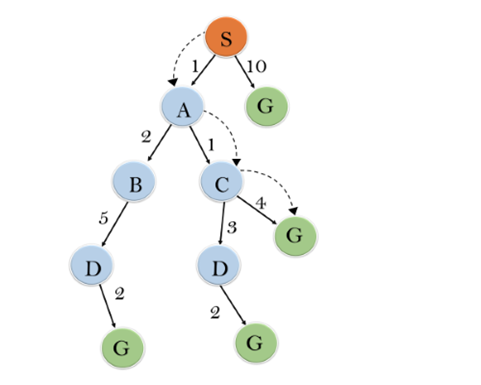
初始化: {(S, 5)}
疊代1: {(S—> A, 4), (S—>G, 10)}
疊代2: {(S—> A—>C, 4), (S—> A—>B, 7), (S—>G, 10)}
疊代3: {(S—> A—>C—->G, 6), (S—> A—>C—->D, 11), (S—> A—>B, 7), (S—>G, 10)}
疊代4將給出最終結果，如： S—->A—->C—->G 它提供了成本6的最佳路徑。

要記住的要點：

• A * 演算法返回首先發生的路徑，並且不搜尋所有剩餘路徑。
• A * 演算法的效率取決於啟發式的品質。
• A * 演算法擴充套件滿足條件f(n)的所有節點

完成：

A * 演算法完成，只要：

• 分支因子是有限的。
• 每項行動的成本都是固定的。

最佳：

如果遵循以下兩個條件，A *搜尋演算法是最佳的：

• 可接受：第一個要求最優的條件是h(n)應該是A * 樹搜尋的可接受的啟發式演算法。可接受的啟發式演算法本質上是樂觀的。
• 一致性：第二個必需條件是僅A * 圖搜尋的一致性。

如果啟發式函式是可接受的，則A * 樹搜尋將始終找到最低成本路徑。

時間複雜度：A * 搜尋演算法的時間複雜度取決於啟發式函式，並且擴充套件的節點數量是指數d的深度的指數。因此，時間複雜度為O(b ^ d)，其中b是分支因子。

空間複雜度：A *搜尋演算法的空間複雜度為O(b ^ d)