PyTorch遞回神經網路

遞迴神經網路是一種遵循順序方法的深度學習導向演算法。在神經網路中，我們總是假設每個輸入和輸出都獨立於所有其他層。這些型別的神經網路被稱為迴圈，因為它們以順序方式執行數學計算，完成一個接一個的任務。

下圖說明了迴圈神經網路的完整方法和工作 -

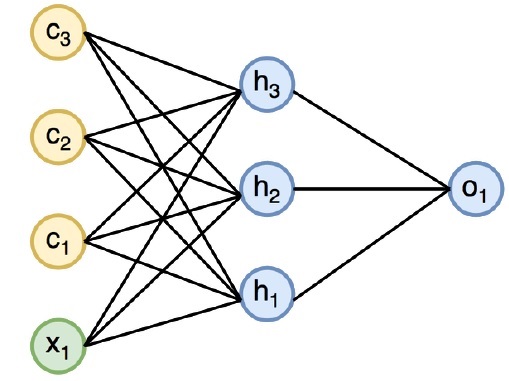
在上圖中，c1，c2，c3和x1是包括一些隱藏輸入值的輸入，即輸出o1的相應輸出的h1，h2和h3。現在將專注於實現PyTorch，以在遞回神經網路的幫助下建立正弦波。

在訓練期間，將遵循模型的培訓方法，一次只有一個資料點。輸入序列x由20個資料點組成，並且目標序列與輸入序列相同。

第1步

使用以下程式碼匯入實現遞回神經網路的必要包 -

import torch
from torch.autograd import Variable
import numpy as np
import pylab as pl
import torch.nn.init as init

第2步
設定模型超引數，輸入層的大小設定為7。將有6個上下文神經元和1個輸入神經元用於建立目標序列。

dtype = torch.FloatTensor
input_size, hidden_size, output_size = 7, 6, 1
epochs = 300
seq_length = 20
lr = 0.1
data_time_steps = np.linspace(2, 10, seq_length + 1)
data = np.sin(data_time_steps)
data.resize((seq_length + 1, 1))

x = Variable(torch.Tensor(data[:-1]).type(dtype), requires_grad=False)
y = Variable(torch.Tensor(data[1:]).type(dtype), requires_grad=False)

我們將生成訓練資料，其中x是輸入資料序列，y是所需的目標序列。

第3步

使用具有零均值的正態分布在遞回神經網路中初始化權重。W1表示接受輸入變數，w2表示生成的輸出，如下所示 -

w1 = torch.FloatTensor(input_size, 
hidden_size).type(dtype)
init.normal(w1, 0.0, 0.4)
w1 = Variable(w1, requires_grad = True)
w2 = torch.FloatTensor(hidden_size, output_size).type(dtype)
init.normal(w2, 0.0, 0.3)
w2 = Variable(w2, requires_grad = True)

第4步

現在，建立一個唯一定義神經網路的前饋功能非常重要。

def forward(input, context_state, w1, w2):
   xh = torch.cat((input, context_state), 1)
   context_state = torch.tanh(xh.mm(w1))
   out = context_state.mm(w2)
   return (out, context_state)

第5步

下一步是開始迴圈神經網路正弦波實現的訓練過程。外迴圈遍歷每個迴圈，內迴圈遍歷序列元素。在這裡，還將計算均方誤差(MSE)，它有助於預測連續變數。

for i in range(epochs):
   total_loss = 0
   context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = True)
   for j in range(x.size(0)):
      input = x[j:(j+1)]
      target = y[j:(j+1)]
      (pred, context_state) = forward(input, context_state, w1, w2)
      loss = (pred - target).pow(2).sum()/2
      total_loss += loss
      loss.backward()
      w1.data -= lr * w1.grad.data
      w2.data -= lr * w2.grad.data
      w1.grad.data.zero_()
      w2.grad.data.zero_()
      context_state = Variable(context_state.data)
   if i % 10 == 0:
      print("Epoch: {} loss {}".format(i, total_loss.data[0]))

context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = False)
predictions = []

for i in range(x.size(0)):
   input = x[i:i+1]
   (pred, context_state) = forward(input, context_state, w1, w2)
   context_state = context_state
   predictions.append(pred.data.numpy().ravel()[0])

第6步
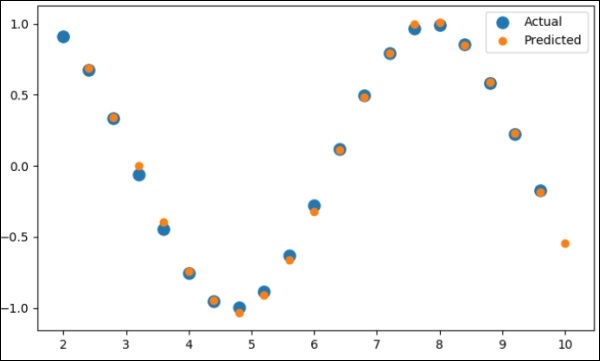
現在，以正確的方式繪製正弦波。

pl.scatter(data_time_steps[:-1], x.data.numpy(), s = 90, label = "Actual")
pl.scatter(data_time_steps[1:], predictions, label = "Predicted")
pl.legend()
pl.show()

上述過程的輸出如下 -