一.基本形式

給定由d個屬性描述的範例 x= (x1; x2; …; xd) ,其中 xi 是 x 在第 i 個屬性上的取值, 線性模型(inear model) 試圖學得一個通過屬性的線性組合來進行預測的函數,即: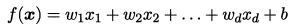

一般用向量形式寫成：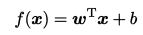

其中 w= (w1;w;…;wd). w和b學得之後，模型就得以確定.

線性模型具有良好的可解釋性（comprehensibility），每個屬性對應的權重可以理解爲它對預測的重要性，並且建模較爲簡單，許多功能更爲強大的非線性模型（nonlinear model）都是線上性模型的基礎上引入層級結構或高維對映得到的。

本章介紹幾種經典的線性模型.我們先從迴歸任務開始，然後討論二分類和多分類任務.

二.線性迴歸

給定數據集 D = {(x1,y1), (x2,y2))…,.(xm,ym)} ,其中 xi = (xi1;xi…;xid), yi∈R .「 線性迴歸」(linear regression) 試圖學得一個線性模型以儘可能準確地預測實值輸出標記.

2.1 離散屬性連續化

由於不同模型對數據的要求不一樣，在建模之前，我們需要對數據做相應的處理。一般的線性迴歸模型要求屬性的數據型別爲連續值，故需要對離散屬性進行連續化。

具體分兩種情況：

1. 屬性值之間有序：也即屬性值有明確的大小關係，比方說把二值屬性「身高」的取值 {高，矮} 可轉化爲 {1.0，0.0}，三值屬性 「高度」的取值 {高，中，低} 轉換（編碼）爲 {1.0，0.5，0.0}；

2. 屬性值之間無序：若該屬性有 k 個屬性值，則通常把它轉換爲 k 維向量（把1個屬性擴充套件爲k個屬性），比方說把無序離散屬性 「商品」 的取值 {牙膏，牙刷，毛巾} 轉換爲 (0，0，1)，(0，1，0)，(1，0，0)。 這種做法在 自然語言處理 和 推薦系統 實現中很常見，屬性 「單詞」 和 「商品」 都是無序離散變數，在建模前往往需要把這樣的變數轉換爲啞變數，否則會引入不恰當的序關係，從而影響後續處理（比如距離的計算 。

補充：對應於離散屬性連續化，自然也有 連續屬性離散化，比方說決策樹建模就需要將連續屬性離散化。此外，在作圖觀察數據分佈特徵時，往往也需要對連續屬性進行離散化處理（比方說畫直方圖）。

2.2 最小二乘法

迴歸任務最常用的效能度量是 均方誤差（mean squared error, MSE），亦稱 平方損失（square loss）。首先介紹 單變數線性迴歸，試想我們要在二維平面上擬合一條曲線，則每個樣例（即每個點）只包含一個實值屬性（x值）和一個實值輸出標記（y值），此時均方誤差可定義爲：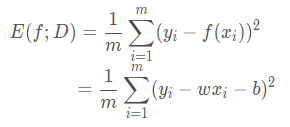

有時我們會把這樣描述模型總誤差的式子稱爲 損失函數 或者 目標函數（當該式是優化目標的時候）。這個函數的自變數是模型的參數 w 和 b。由於給定訓練集時，樣本數 m 是一個確定值，也即常數，所以可以把 1/m這一項拿走。

最小二乘法（least square method） 就是基於均方誤差最小化來進行模型求解的一種方法，尋找可使損失函數值最小的參數 w 和 b 的過程稱爲最小二乘 參數估計（parameter estimation）。線上性迴歸中，最小二乘法就是試圖找到一條直線，使所有樣本到直線上的歐氏距離之和最小。

通過對損失函數分別求參數 w 和 b 的偏導，並且令導數爲0，可以得到這兩個參數的 閉式（closed-form）解（也即解析解）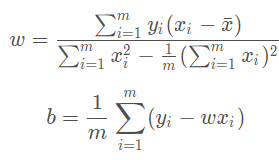

關於最小二乘法的詳細推導過程，可以去看下面 下麪這篇文章：

• 最小二乘法求迴歸直線方程的詳細推導過程: https://blog.csdn.net/qq_43328040/article/details/106930113

2.3 多元線性迴歸

前面是直線擬合，樣例只有一個屬性。對於樣例包含多個屬性的情況，我們就要用到 多元線性迴歸（multivariate linear regression）（又稱作多變數線性迴歸）了。

令^w = (W; b)，把數據集表示爲 m * (d + 1) 大小的矩陣 X，
每一行對應一個樣例，前 d 列是樣例的 d 個屬性，最後一列恆置爲1，對應偏置項。樣例的實值標記也寫作向量形式，記作 y。則此時損失函數爲：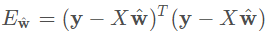

同樣使用最小二乘法進行參數估計，首先對 ^w 求導：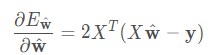

解析

令該式值爲0可得到 ^w 的閉式解：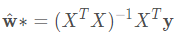

這就要求 (XT)X 必須是可逆矩陣, 也即必須是 滿秩矩陣（full-rank matrix） 或者是 正定矩陣（positive definite matrix），這是線性代數方面的知識，書中並未展開討論。但是！現實任務中 (XT)X 往往不是滿秩的, 很多時候 X 的列數很多，甚至超出行數（例如 推薦系統，商品數是遠遠超出使用者數的），此時 (XT)X 顯然不滿秩，會解出多個 ^w。這些解都能使得均方誤差最小化，選擇哪一個解作爲輸出，這時就需要由學習演算法的 歸納偏好決定了，常見的做法是引入 正則化（regularization） 項。

2.4 廣義線性模型

除了直接讓模型預測值逼近實值標記 y，我們還可以讓它逼近 y 的衍生物，這就是 廣義線性模型（generalized linear model） 的思想，也即：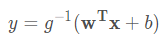

其中 g(.) 稱爲 聯繫函數（link function），要求單調可微。使用廣義線性模型我們可以實現強大的 非線性函數對映 功能。比方說 對數線性迴歸（log-linear regression），令 g(.) = ln(.)，此時模型預測值對應的是 實值標記在指數尺度上的變化：

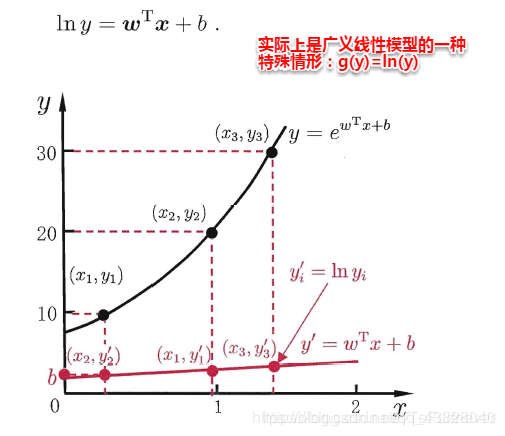
三.對數機率迴歸（邏輯迴歸）

前面說的是線性模型在迴歸學習方面的應用，這節開始就是討論分類學習了。

線性模型的輸出是一個實值，而分類任務的標記是離散值，怎麼把這兩者聯繫起來呢？

其實廣義線性模型已經給了我們答案，我們要做的就是 找到一個單調可微的聯繫函數，把兩者聯繫起來。

對於一個二分類任務，比較理想的聯繫函數是 單位階躍函數（unit-step function）：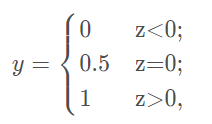

但是單位階躍函數不連續，所以不能直接用作聯繫函數。這時思路轉換爲 如何在一定程度上近似單位階躍函數 呢？對數機率函數（logistic function） 正是我們所需要的常用的替代函數（注意這裏的 y 依然是實值）：

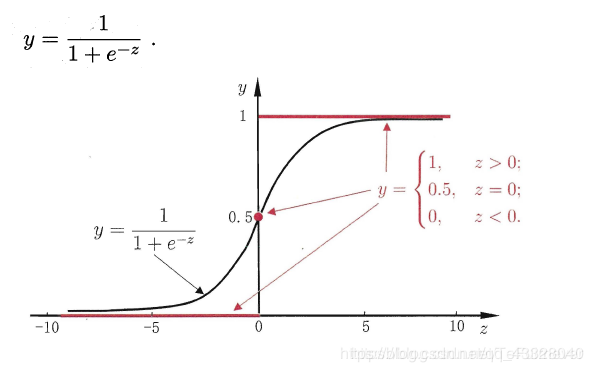
對數機率函數有時也稱爲對率函數，是一種 Sigmoid函數（即形似S的函數）。將它作爲 g(.) 代入廣義線性模型可得：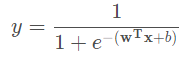

該式可以改寫爲：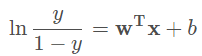

其中，y / (1 - y) 稱作 機率（odds） 我們可以把 y 理解爲該樣本是正例的概率，把 1−y 理解爲該樣本是反例的概率，而機率表示的就是 該樣本作爲正例的相對可能性。 若機率大於1，則表明該樣本更可能是正例。對機率取對數就得到 對數機率（log odds，也稱爲logit）。機率大於1時，對數機率是正數。

由此可以看出，對數機率迴歸的實質使用線性迴歸模型的預測值逼近分類任務真實標記的對數機率。

它有幾個優點：

1. 直接對分類的概率建模，無需事先假設數據分佈，從而避免了假設分佈不準 不準確所帶來的問題；
2. 不僅可預測出「類別」，還能得到該預測的近似概率，這對一些利用概率輔助決策的任務很有用；
3. 對數機率函數是任意階可導的凸函數，有很好的數學性質，有許多數值優化演算法都可以求出最優解。

3.1 最大似然估計

有了預測函數之後，我們需要關心的就是怎樣求取模型參數了。這裏介紹一種與最小二乘法異曲同工的辦法，叫做 極大似然法（maximum likelihood method）。

前面說到可以把 y 理解爲一個樣本是正例的概率，把 1 - y 理解爲一個樣本是反例的概率。而所謂極大似然，就是最大化預測事件發生的概率，也即 最大化所有樣本的預測概率之積。 令 p(c = 1|x) 和 p(c = 0|x) 分別表示 y 和 1 - y。

簡單變換一下公式，可以得到：

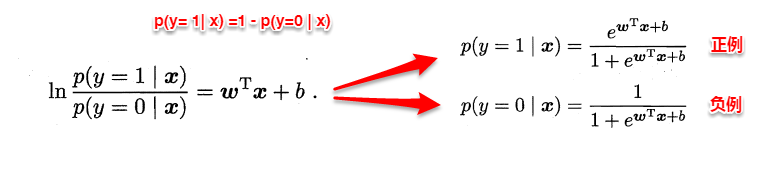
但是！由於預測概率都是小於1的，如果直接對所有樣本的預測概率求積，所得的數會非常非常小，當樣例數較多時，會超出精度限制。所以，一般來說會對概率取對數，得到 對數似然（log-likelihood），此時 求所有樣本的預測概率之積就變成了求所有樣本的對數似然之和。對率迴歸模型的目標就是最大化對數似然，對應的似然函數是：

可以理解爲若標記爲正例，則加上預測爲正例的概率，否則加上預測爲反例的概率。其中 β = (w；b)。

對該式求導，令導數爲0可以求出參數的最優解。特別地，我們會發現似然函數的導數和損失函數是等價的，所以說 最大似然解等價於最小二乘解。最大化似然函數等價於最小化損失函數：

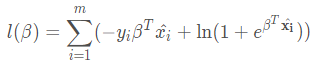
解析：

 

四.線性判別分析（LDA）

 

線性判別分析(Linear Discriminant Analysis, 簡稱LDA) 是一種經典的線性學習方法，在二分類問題上因爲最早由(Fisher, 1936] 提出，亦稱「Fisher 判別分析」

LDA的思想非常樸素:給定訓練樣例集, 設法將樣例投影到一條直線上, 使得同類樣例的投影點儘可能接近、異類樣例的投影點儘可能遠離;在對新樣本進行分類時，將其投影到同樣的這條直線上，再根據投影點的位置來確定新樣本的類別.圖3.3給出了一個二維示意圖.

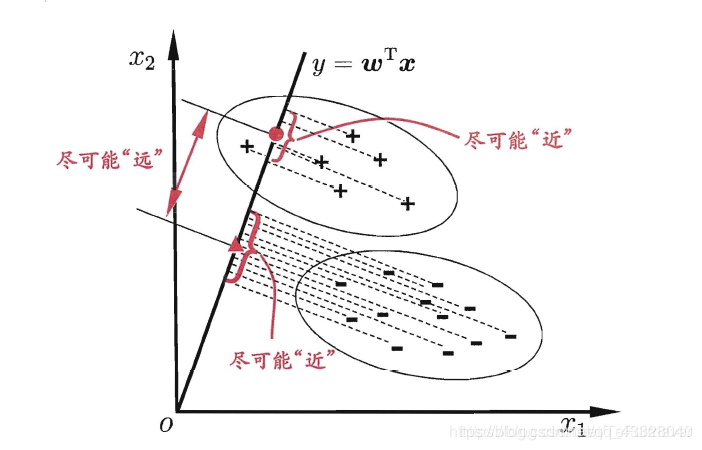
如何實現呢？

• 首先，同類樣例的投影值儘可能相近意味着 同類樣例投影值的協方差應儘可能小；
• 然後，異類樣例的投影值儘可能遠離意味着 異類樣例投影值的中心應儘可能大。
• 合起來，就等價於最大化：
  

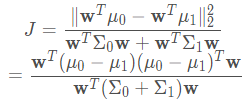
其中，分子的 μi 表示第 i 類樣例的 均值向量（即表示爲向量形式後對各維求均值所得的向量）。分子表示的是兩類樣例的均值向量投影點（也即類中心）之差的 ℓ2 範數的平方，這個值越大越好。 分母中的 Σi 表示第 i 類樣例的 協方差矩陣。 分母表示兩類樣例投影後的協方差之和，這個值越小越好。

定義 類內散度矩陣（within-class scatter matrix）：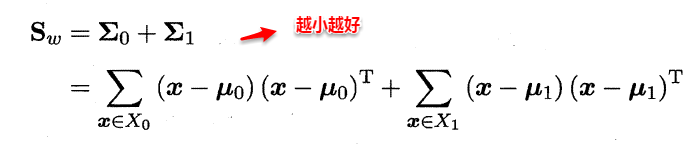

定義 類間散度矩陣（between-class scatter matrix）：

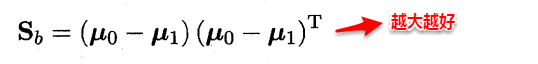
這兩個矩陣的規模都是 d×d ，其中 d 是樣例的維度（屬性數目）。於是可以重寫目標函數爲：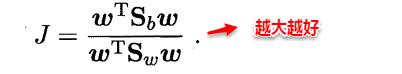
也即 Sb 和 Sw的 廣義瑞利熵（generalized Rayleigh quotient）。

可以注意到，分子和分母中 w 都是二次項，因此，最優解與 w 的大小無關，只與方向有關。令分母爲1，用拉格朗日乘子法把約束轉換爲方程，再稍加變換我們便可以得出：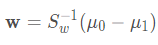

但一般不直接對矩陣 Sw 求逆，而是採用奇異值分解的方式。

從而分類問題轉化爲最佳化求解w的問題，當求解出w後，對新的樣本進行分類時，只需將該樣本點投影到這條直線上，根據與各個類別的中心值進行比較，從而判定出新樣本與哪個類別距離最近。

求解w的方法如下所示，使用的方法爲λ乘子。

五.類別不平衡問題

**類別不平衡（class-imbalance） **問題非常普遍，比方說推薦系統中使用者購買的商品（通常視作正例）和使用者未購買的商品（通常視作反例）比例是極爲懸殊的。如果直接用類別不平衡問題很嚴重的數據集進行訓練，所得模型會嚴重偏向所佔比例較大的類別。本節預設正類樣例較少，負類樣例較多。

這裏主要介紹三種做法：

5.1 欠採樣

欠採樣（undersampling） 針對的是負類，也即移取訓練集的部分反例，使得正類和負類的樣例數目相當。由於丟掉了大量反例，所以 時間開銷也大大減少。但是帶來一個問題就是，隨機丟棄反例可能會丟失一些重要資訊。書中提到一種解決方法是利用 整合學習機制 機製，將反例劃分爲多個集合，用於訓練不同的模型，從而使得 對每個模型來說都進行了欠採樣，但全域性上並無丟失重要資訊。

5.2 過採樣

過採樣（oversampling） 針對的是正類，也即增加訓練集的正例，使得正類和負類的樣例數目相當。過採樣的時間開銷會增大很多， 因爲需要引入很多正例。注意！過採樣 不能簡單地通過重複正例來增加正例的比例，這樣會引起嚴重的過擬合問題。一種較爲常見的做法是對已有正例進行 插值 來產生新的正例。

5.3闕值移動

閾值移動（threshold-moving） 利用的是 再縮放 思想。回想前面對數機率迴歸中，機率 y / (1 - y) 表示正例的相對可能性，我們預設以1作爲閾值，其實是假設了樣本的真實分佈爲正例反例各一半。但這可能不是真相，假設我們有一個存在類別不平衡問題的訓練集，正例數目爲 m+, 反例數目爲 m-，可以重定義：

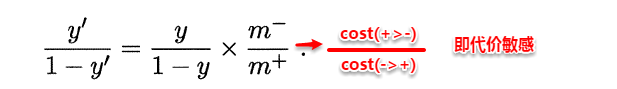
這就是 再縮放（rescaling）。 當機率大於 m+ / m- 時就預測爲正例。但必須注意，這種思想是 基於觀測機率近似真實機率這一假設 的，現實任務中這一點未必成立。

如果對軟體測試有興趣，想瞭解更多的測試知識，解決測試問題,以及入門指導，
幫你解決測試中遇到的困惑，我們這裏有技術高手。如果你正在找工作或者剛剛學校出來，
又或者已經工作但是經常覺得難點很多，覺得自己測試方面學的不夠精想要繼續學習的，
想轉行怕學不會的，都可以加入我們644956177。
羣內可領取最新軟體測試大廠面試資料和Python自動化、介面、框架搭建學習資料！