【論文翻譯】Deep learning

論文題目：Deep learning
論文來源：Deep learning
翻譯人：BDML@CQUT實驗室

Deep learning

Yann LeCun, Yoshua Bengio & Geoffrey Hinton

Abstract

Deep learning allows computational models that are composed of multiple processing layers to learn representations of data with multiple levels of abstraction. These methods have dramatically improved the state-of-the-art in speech rec­ognition, visual object recognition, object detection and many other domains such as drug discovery and genomics. Deep learning discovers intricate structure in large data sets by using the backpropagation algorithm to indicate how a machine should change its internal parameters that are used to compute the representation in each layer from the representation in the previous layer. Deep convolutional nets have brought about breakthroughs in processing images, video, speech and audio, whereas recurrent nets have shone light on sequential data such as text and speech.

摘要

深度學習能夠讓那些由多個處理層組成的計算模型學習如何表示高度抽象的數據。這些方法極大地改善了語音識別，視覺物件識別，物件檢測以及許多其他領域的最新技術，例如藥物發現和基因組學。深度學習通過使用BP演算法來指示機器如何更改用於計算每層表示的內部參數，這些參數用於計算前一層的表示，從而發現大數據中的複雜結構。深層折積網路在處理影象，視訊，語音和音訊方面帶來了突破，而遞回網路則在諸如文字和語音之類的序列數據等方面展現潛力。

正文

Machine-learning technology powers many aspects of modern society: from web searches to content filtering on social net­works to recommendations on e-commerce websites, and it is increasingly present in consumer products such as cameras and smartphones. Machine-learning systems are used to identify objects in images, transcribe speech into text, match news items, posts or products with users’ interests, and select relevant results of search. Increasingly, these applications make use of a class of techniques called deep learning.

機器學習技術爲現代社會的各個方面提供了強大的動力：從網路搜尋到社羣網路上的內容過濾，再到電子商務網站上的推薦，並且它在諸如相機和智慧手機之類的消費產品中越來越多地出現。 機器學習系統用於識別影象中的物件，將語音轉換爲文字，匹配新聞元素，根據使用者興趣匹配職位和產品，選擇相關的搜尋結果。這些應用程式越來越多地使用一類稱爲深度學習的技術。

Conventional machine-learning techniques were limited in their ability to process natural data in their raw form. For decades, con­structing a pattern-recognition or machine-learning system required careful engineering and considerable domain expertise to design a fea­ture extractor that transformed the raw data (such as the pixel values of an image) into a suitable internal representation or feature vector from which the learning subsystem, often a classifier, could detect or classify patterns in the input.

傳統的機器學習技術在處理未加工過的數據方面受到限制。幾十年來，構建一個模式識別或機器學習系統需要仔細的工程設計和相當多的專業知識來設計一個特徵提取器，它將原始數據（例如影象的畫素值）轉換成合適的內部表示或特徵向量，子學習系統通常是分類器，可以檢測或分類輸入的樣本。

Representation learning is a set of methods that allows a machine to be fed with raw data and to automatically discover the representations needed for detection or classification. Deep-learning methods are representation-learning methods with multiple levels of representa­tion, obtained by composing simple but non-linear modules that each transform the representation at one level (starting with the raw input) into a representation at a higher, slightly more abstract level. With the composition of enough such transformations, very complex functions can be learned. For classification tasks, higher layers of representation amplify aspects of the input that are important for discrimination and suppress irrelevant variations. An image, for example, comes in the form of an array of pixel values, and the learned features in the first layer of representation typically represent the presence or absence of edges at particular orientations and locations in the image. The second layer typically detects motifs by spotting particular arrangements of edges, regardless of small variations in the edge positions. The third layer may assemble motifs into larger combinations that correspond to parts of familiar objects, and subsequent layers would detect objects as combinations of these parts. The key aspect of deep learning is that these layers of features are not designed by human engineers: they are learned from data using a general-purpose learning procedure.

特徵學習是一組方法，能讓機器通過未加工數據自動發現並總結檢測和分類所需的「特徵描述」。而深度學習就是具有多層次「特徵描述」的特徵學習，通過一些簡單但非線性的模組將每一層「特徵描述」（從未加工的數據開始）轉化爲更高一層的、稍微更抽象一些的「特徵描述」。使用足夠多的這樣的轉化，那些非常複雜的函數也可以被學習。對於分型別任務而言，更高層次的「特徵描述」能增強對識別能力非常重要的輸入數據的各個方面，同時削弱（輸入數據裡）無關緊要的變化因素。比如一個影象以畫素陣列的形式輸入，第一層的「特徵描述」通常會表示影象的特定位置或方向是否存在邊界，第二層可能會將圖案拼湊起來以使它們和一些熟悉的物體的某部分相一致，之後的層次則會將這些部分組合起來並據此識別物體。深度學習的關鍵在於這些層次的特徵不是人工設計的：它們是使用一種通用的學習步驟從數據中學習的。

Deep learning is making major advances in solving problems that have resisted the best attempts of the artificial intelligence commu­nity for many years. It has turned out to be very good at discovering intricate structures in high-dimensional data and is therefore applica­ble to many domains of science, business and government. In addition to beating records in image recognition and speech recognition, it has beaten other machine-learning techniques at predicting the activ­ity of potential drug molecules, analysing particle accelerator data, reconstructing brain circuits, and predicting the effects of mutations in non-coding DNA on gene expression and disease. Perhaps more surprisingly, deep learning has produced extremely promising results for various tasks in natural language understanding, particularly topic classification, sentiment analysis, question answering and language translation.

在解決人工智慧界多年來盡最大努力都無法解決的問題方面，深度學習正在取得重大進展。 事實證明，它非常善於發現高維數據中的複雜結構，因此適用於科學，商業和政府的許多領域。除了在影象識別和語音識別中打破記錄外，它在預測潛在藥物分子的活性，分析粒子加速器數據，重建腦回路以及預測非編碼DNA突變對基因表達和疾病的影響方面還擊敗了其他機器學習技術。也許更令人驚訝的是，深度學習爲自然語言理解中的各種任務（尤其是主題分類，情感分析，問題解答和語言翻譯）取得了了非常有希望的結果。

We think that deep learning will have many more successes in the near future because it requires very little engineering by hand, so it can easily take advantage of increases in the amount of available com­putation and data. New learning algorithms and architectures that are currently being developed for deep neural networks will only acceler­ate this progress.

我們認爲深度學習將在不久的將來取得更多的成功，因爲它只需要很少的手工操作，因此可以輕鬆利用可用計算和數據量的增加。 當前正在爲深度神經網路開發的新的學習演算法和體系結構只會加速這一進展。

Supervised learning

The most common form of machine learning, deep or not, is super­vised learning. Imagine that we want to build a system that can classify images as containing, say, a house, a car, a person or a pet. We first collect a large data set of images of houses, cars, people and pets, each labelled with its category. During training, the machine is shown an image and produces an output in the form of a vector of scores, one for each category. We want the desired category to have the highest score of all categories, but this is unlikely to happen before training. We compute an objective function that measures the error (or dis­tance) between the output scores and the desired pattern of scores. The machine then modifies its internal adjustable parameters to reduce this error. These adjustable parameters, often called weights, are real numbers that can be seen as ‘knobs’ that define the input–output func­tion of the machine. In a typical deep-learning system, there may be hundreds of millions of these adjustable weights, and hundreds of millions of labelled examples with which to train the machine.

監督學習

機器學習最常見的形式，無論深度與否，都是監督學習。想象一下，我們想建立一個可以將影象分類爲包含房屋，汽車，人或寵物的系統。我們首先收集了房子，汽車，人和寵物大量的影象的數據集，每一個都有其分類的標籤。在訓練過程中，機器會顯示一個影象，並以向量形式的分數生成輸出，每個類別對應一個分數。我們希望理想的類別在所有類別中得分最高，但這不可能在訓練前發生。我們計算一個目標函數來度量輸出分數和期望的分數模式之間的誤差（或距離）。然後，機器修改其內部可調參數以減少此誤差。這些可調參數，通常稱爲權重，是一個實數，可以看作是定義機器輸入輸出功能的「旋鈕」。在典型的深度學習系統中，可能有數以億計的可調權重和標籤樣本，以用於訓練機器。

To properly adjust the weight vector, the learning algorithm com­putes a gradient vector that, for each weight, indicates by what amount the error would increase or decrease if the weight were increased by a tiny amount. The weight vector is then adjusted in the opposite direc­tion to the gradient vector.

爲了正確地調整權重向量，該學習演算法計算每個權重的梯度向量，表示如果權重稍微增加一點，誤差會增加或減少多少。然後在與梯度向量相反的方向上調整權重向量。

The objective function, averaged over all the training examples, can be seen as a kind of hilly landscape in the high-dimensional space of weight values. The negative gradient vector indicates the direction of steepest descent in this landscape, taking it closer to a minimum, where the output error is low on average.

在所有訓練樣本上取平均值的目標函數，可以看作是一種高維權重空間中的多變地形。負梯度向量表示該地形中下降最快的方向，使其更接近最小值，平均輸出誤差最低。

In practice, most practitioners use a procedure called stochastic gradient descent (SGD). This consists of showing the input vector for a few examples, computing the outputs and the errors, computing the average gradient for those examples, and adjusting the weights accordingly. The process is repeated for many small sets of examples from the training set until the average of the objective function stops decreasing. It is called stochastic because each small set of examples gives a noisy estimate of the average gradient over all examples. This simple procedure usually finds a good set of weights surprisingly quickly when compared with far more elaborate optimization tech­niques. After training, the performance of the system is measured on a different set of examples called a test set. This serves to test the generalization ability of the machine — its ability to produce sensible answers on new inputs that it has never seen during training.

實際上，大多數從業者使用稱爲隨機梯度下降（SGD）的演算法。它包括了提供一些樣本的輸入向量，計算輸出和誤差，計算這些樣本的平均梯度，並相應地調整權重。從訓練集中的許多小樣本重複這個過程，直到目標函數的平均值停止下降。之所以被稱爲隨機的，是因爲每個小樣本集都給出了所有樣本的平均梯度的噪聲估計。與其他精心設計的優化技術相比，這個簡單的過程通常以驚人的速度找到一組好的權重。在訓練之後，系統的效能將在一組稱爲測試集的不同樣本上進行測量。這用於測試機器的泛化能力，即它對新輸入產生合理答案的能力，而這是在訓練中從未見過的。

Many of the current practical applications of machine learning use linear classifiers on top of hand-engineered features. A two-class linear classifier computes a weighted sum of the feature vector components. If the weighted sum is above a threshold, the input is classified as belonging to a particular category.

目前機器學習的許多實際應用是在手工設計的特徵之上使用線性分類器。兩類線性分類器計算特徵向量分量的加權和。如果加權和高於閾值，則輸入被歸類爲一個特定的類別中。

Since the 1960s we have known that linear classifiers can only carve their input space into very simple regions, namely half-spaces sepa­rated by a hyperplane19. But problems such as image and speech recog­nition require the input–output function to be insensitive to irrelevant variations of the input, such as variations in position, orientation or illumination of an object, or variations in the pitch or accent of speech, while being very sensitive to particular minute variations (for example, the difference between a white wolf and a breed of wolf-like white dog called a Samoyed). At the pixel level, images of two Samoyeds in different poses and in different environments may be very different from each other, whereas two images of a Samoyed and a wolf in the same position and on similar backgrounds may be very similar to each other. A linear classifier, or any other ‘shallow’ classifier operating on raw pixels could not possibly distinguish the latter two, while putting the former two in the same category. This is why shallow classifiers require a good feature extractor that solves the selectivity–invariance dilemma — one that produces representations that are selective to the aspects of the image that are important for discrimination, but that are invariant to irrelevant aspects such as the pose of the animal. To make classifiers more powerful, one can use generic non-linear features, as with kernel methods, but generic features such as those arising with the Gaussian kernel do not allow the learner to general­ize well far from the training examples. The conventional option is to hand design good feature extractors, which requires a consider­able amount of engineering skill and domain expertise. But this can all be avoided if good features can be learned automatically using a general-purpose learning procedure. This is the key advantage of deep learning.

從1960年以來我們發現線性分類器只能把它們的輸入空間分割成非常簡單的區域，也就是用一個超平面把輸入空間對半分開。但類似於影象識別和語音識別的問題需要一個對輸入數據中那些不重要的變化不敏感的輸入-輸出函數，比如物體的位置、方向或者是光照情況，又或者是語音識別中音高或口音的差異，但同時，所得的函數還需要對一些非常微小的變化特別敏感（比如，一隻白色的狼和一隻和狼很相似的白色大狗薩摩耶）。在畫素的層次上，不同影象上的姿勢和所處環境不同的薩摩耶或許也會顯得非常不同，然而不同影象上處於相同位置和相似背景中的薩摩耶和狼卻可能非常相似。線性分類器，或者是任何其他在原始畫素上進行操作的淺層分類器都不太可能在區別後兩者的同時把前兩者歸爲一類。這就是爲什麼淺層分類器需要一個好的特徵提取器，通過提供對識別重要的但對無關變數不敏感的（例如動物的姿勢）、嚴格篩選的影象特徵來解決選擇不變性的困難。爲了讓分類器效能更強，我們可以使用一些通用的非線性特徵，比如通過核方法得到的（譯註：此處原文對「核方法」有第20個參照說明，可在原文檢視或直接搜尋關鍵詞），但如高斯核得到的通用特徵無法讓學習器得到很好的泛化概括結果。傳統的選擇是，手工設計一個良好的特徵提取器，這需要大量的工程技巧和專業知識。但如果能用通用的學習步驟自動地學習出一些良好的特徵，這些（麻煩）都可以被避免。這就是深度學習最關鍵的優勢。

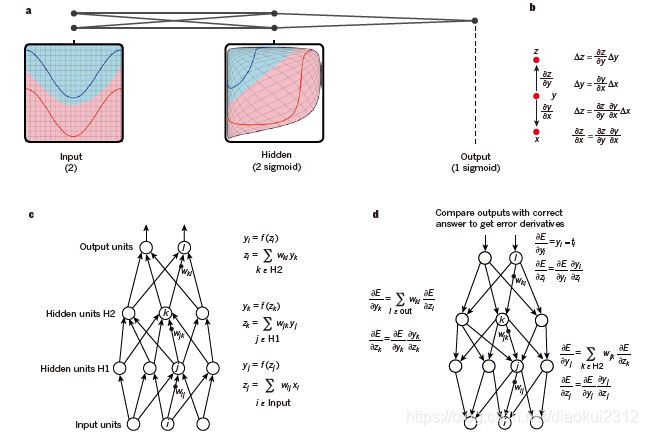
Figure 1 | Multilayer neural networks and backpropagation.

a, A multi-layer neural network (shown by the connected dots) can distort the input space to make the classes of data (examples of which are on the red and blue lines) linearly separable. Note how a regular grid (shown on the left) in input space is also transformed (shown in the middle panel) by hidden units. This is an illustrative example with only two input units, two hidden units and one output unit, but the networks used for object recognition or natural language processing contain tens or hundreds of thousands of units. Reproduced with permission from C. Olah (http://colah.github.io/).

b, The chain rule of derivatives tells us how two small effects (that of a small change of x on y, and that of y on z) are composed. A small change Δx in x gets transformed first into a small change Δy in y by getting multiplied by ∂y/∂x (that is, the definition of partial derivative). Similarly, the change Δy creates a change Δz in z. Substituting one equation into the other gives the chain rule of derivatives — how Δx gets turned into Δz through multiplication by the product of ∂y/∂x and ∂z/∂x. It also works when x, y and z are vectors (and the derivatives are Jacobian matrices).

c, The equations used for computing the forward pass in a neural net with two hidden layers and one output layer, each constituting a module through which one can backpropagate gradients. At each layer, we first compute the total input z to each unit, which is a weighted sum of the outputs of the units in the layer below. Then a non-linear function f(.) is applied to z to get the output of the unit. For simplicity, we have omitted bias terms. The non-linear functions used in neural networks include the rectified linear unit (ReLU) f(z) = max(0,z), commonly used in recent years, as well as the more conventional sigmoids, such as the hyberbolic tangent, f(z) = (exp(z) − exp(−z))/(exp(z) + exp(−z)) and logistic function logistic, f(z) = 1/(1 + exp(−z)).

d, The equations used for computing the backward pass. At each hidden layer we compute the error derivative with respect to the output of each unit, which is a weighted sum of the error derivatives with respect to the total inputs to the units in the layer above. We then convert the error derivative with respect to the output into the error derivative with respect to the input by multiplying it by the gradient of f(z). At the output layer, the error derivative with respect to the output of a unit is computed by differentiating the cost function. This gives yl − tl if the cost function for unit l is 0.5(yl − tl)2, where tl is the target value. Once the ∂E/∂zk is known, the error-derivative for the weight wjk on the connection from unit j in the layer below is just yj ∂E/∂zk.

圖1 多層神經網路和反向傳播

a、多層神經網路（由連線點表示）可以扭曲輸入空間，使數據類別（紅色和藍色線表示的樣本）線性可分離。注意輸入空間中的規則網格（如左圖所示）是如何通過隱層進行變換的（如中間面板所示）。這是一個說明性的例子，只有兩個輸入節點，兩個隱節點和一個輸出節點，但是用於物件識別或自然語言處理的網路包含成千上萬個節點。經C.Olah許可(http://colah.github.io/)可重新構建這個圖.

b、導數的鏈式法則告訴我們兩個小效應（x對y的微小變化，y對z的微小變化）是如何組織到一起的。首先將x中的微小變化Δx通過乘以∂y/∂x（即偏導數的定義）轉換爲y的變化量Δy。類似地，變化量Δy會在z中產生一個變化量Δz。將一個方程代入另一個方程就得到了導數的鏈式規則——Δx是如何通過∂y/∂x 和∂z/∂x相乘而變成Δz的。當x、y和z是向量（導數是雅可比矩陣）時，它同樣適用。

c、 用於計算神經網路前向傳播的公式，該神經網路有兩個隱層和一個輸出層，每一層構成一個模組，通過該模組可以反向傳播梯度。在每一層，我們首先計算每個節點的總輸入z，這是下一層節點輸出的加權和。然後將一個非線性函數f（.）應用於z得到節點的輸出。爲了簡單起見，我們省略了偏差項。神經網路中使用的非線性函數包括近年來常用的校正線性單元(ReLU) f(z)=max(0,z)，以及更傳統的sigmoid，如雙曲線正切函數f(z) = (exp(z) − exp(−z))/(exp(z) + exp(−z))和logistic函數，f(z) = 1/(1 + exp(−z)).

d、計算反向傳播的公式。在每個隱層，我們計算每個單元的輸出的誤差導數，它是相對於上一層單元的總輸入的誤差導數的加權和。然後我們將輸出層的誤差導數乘以f(z)的梯度，將其轉換爲輸入層的誤差導數。在輸出層，通過對成本函數的微分，計算出輸出單元的誤差導數。如果單元l的成本函數爲0.5(yl − tl)^2，則單元誤差爲yl − tl，其中tl是期望值。一旦∂E/∂zk已知，下一層中來自單元j的連線上的權重wjk的誤差導數僅爲yj∂E/∂zk。

A deep-learning architecture is a multilayer stack of simple mod­ules, all (or most) of which are subject to learning, and many of which compute non-linear input–output mappings. Each module in the stack transforms its input to increase both the selectivity and the invariance of the representation. With multiple non-linear layers, say a depth of 5 to 20, a system can implement extremely intricate func­tions of its inputs that are simultaneously sensitive to minute details — distinguishing Samoyeds from white wolves — and insensitive to large irrelevant variations such as the background, pose, lighting and surrounding objects.

深度學習體系結構是簡單模組的多層棧，其中所有（或大部分）模組都需要學習，還有許多模組計算非線性輸入-輸出對映。棧中的每個模組轉換其輸入，以提高表達的選擇性和不變性。有了一個5到20層的非線性層系統可以實現其輸入的極其複雜的功能，如輸入數據對細節很敏感——區分薩摩耶犬和白狼——並且對大的無關變化不敏感，比如背景、姿勢、光照和周圍的物體。

Backpropagation to train multilayer architectures

From the earliest days of pattern recognition, the aim of research­ers has been to replace hand-engineered features with trainable multilayer networks, but despite its simplicity, the solution was not widely understood until the mid 1980s. As it turns out, multilayer architectures can be trained by simple stochastic gradient descent. As long as the modules are relatively smooth functions of their inputs and of their internal weights, one can compute gradients using the backpropagation procedure. The idea that this could be done, and that it worked, was discovered independently by several different groups during the 1970s and 1980s.

反向傳播來訓練多層體系結構

從模式識別的早期開始，研究人員的目的就是用可訓練的多層網路代替人工設計的特徵，但是儘管多層神經網路很簡單，但直到1980年代中期，該解才被廣泛理解。 事實證明，可以通過簡單的隨機梯度下降來訓練多層體系結構。只要模組是其輸入及其內部權重的相對平滑函數，就可以使用反向傳播過程來計算梯度。在20世紀70年代和80年代，幾個不同的研究小組獨立地發現了可以做到這一點並且起作用的想法。

The backpropagation procedure to compute the gradient of an objective function with respect to the weights of a multilayer stack of modules is nothing more than a practical application of the chain rule for derivatives. The key insight is that the derivative (or gradi­ent) of the objective with respect to the input of a module can be computed by working backwards from the gradient with respect to the output of that module (or the input of the subsequent module) (Fig. 1). The backpropagation equation can be applied repeatedly to propagate gradients through all modules, starting from the output at the top (where the network produces its prediction) all the way to the bottom (where the external input is fed). Once these gradients have been computed, it is straightforward to compute the gradients with respect to the weights of each module.

用反向傳播演算法計算一個目標函數相對於一個多層模組棧的權重的梯度，不過是鏈式求導規則的一個實際應用。核心思想是，目標相對於模組輸入的導數（或梯度）可以通過從相對於模組輸出（或下一層模組輸入）從梯度進行反向運算（圖1）。反向傳播演算法可重複應用於在傳播梯度通過多層體系結構的每一層，從頂部的輸出（網路產生其預測）一直到底部（外部輸入被饋送）。一旦計算出這些梯度，就很容易計算出相對於每個模組權重的梯度。

Many applications of deep learning use feedforward neural net­work architectures (Fig. 1), which learn to map a fixed-size input (for example, an image) to a fixed-size output (for example, a prob­ability for each of several categories). To go from one layer to the next, a set of units compute a weighted sum of their inputs from the previous layer and pass the result through a non-linear function. At present, the most popular non-linear function is the rectified linear unit (ReLU), which is simply the half-wave rectifier f(z) = max(z, 0). In past decades, neural nets used smoother non-linearities, such as tanh(z) or 1/(1 + exp(−z)), but the ReLU typically learns much faster in networks with many layers, allowing training of a deep supervised network without unsupervised pre-training. Units that are not in the input or output layer are conventionally called hidden units. The hidden layers can be seen as distorting the input in a non-linear way so that categories become linearly separable by the last layer (Fig. 1).

深度學習的許多應用使用前饋式神經網路架構（圖1），該神經網路學習將固定大小的輸入（例如，影象）對映到固定大小的輸出（例如，幾個類別中的每一個的概率）。爲了從一層到下一層，計算上一層神經元輸入數據的加權和，並將結果傳遞給一個非線性函數。目前最流行的非線性函數是線性整流函數（ReLU），即半波整流器f（z）=max（z，0）。在過去的幾十年裡，神經網路使用更平滑的非線性函數，例如tanh（z）和1/(1 + exp(−z))，但ReLU通常在多層神經網路中學習得更快，允許在無監督預訓練的情況下訓練有監督的深度網路。不在輸入或輸出層的神經單元通常稱爲隱單元。隱層可以被視爲以非線性方式扭曲輸入數據，使得輸入數據的類別可以在最後一層線性分離（圖1）。

In the late 1990s, neural nets and backpropagation were largely forsaken by the machine-learning community and ignored by the computer-vision and speech-recognition communities. It was widely thought that learning useful, multistage, feature extractors with lit­tle prior knowledge was infeasible. In particular, it was commonly thought that simple gradient descent would get trapped in poor local minima — weight configurations for which no small change would reduce the average error.

在20世紀90年代末，神經網路和反向傳播演算法在很大程度上被機器學習團隊所拋棄，也被計算機視覺和語音識別團隊所忽視。人們普遍認爲，學習有用的、多階段的、具有少量先驗知識的特徵提取器是不可行的。特別是，人們普遍認爲簡單的梯度下降會陷入不良的區域性最小值——權重設定，任何小的變化都會降低平均誤差。

In practice, poor local minima are rarely a problem with large net­works. Regardless of the initial conditions, the system nearly always reaches solutions of very similar quality. Recent theoretical and empirical results strongly suggest that local minima are not a serious issue in general. Instead, the landscape is packed with a combinato­rially large number of saddle points where the gradient is zero, and the surface curves up in most dimensions and curves down in the remainder. The analysis seems to show that saddle points with only a few downward curving directions are present in very large numbers, but almost all of them have very similar values of the objec­tive function. Hence, it does not much matter which of these saddle points the algorithm gets stuck at.

實際上，對於大型網路而言，較差的區域性最小值並不是問題。不管初始條件如何，該系統幾乎總是能獲得效果非常相似的解。最近的理論和經驗結果表明，區域性極小值通常不是一個嚴重的問題。相反，解空間中填充了大量的鞍點（梯度爲零），並且曲面在大多數維度上向上彎曲，而在其餘維度上向下彎曲。分析似乎表明，只有很少幾個向下彎曲方向的鞍點存在很多，但是幾乎所有鞍點的目標函數值都非常相似。因此，演算法陷入這些鞍點中的哪一個都沒關係。

Interest in deep feedforward networks was revived around 2006 by a group of researchers brought together by the Cana­dian Institute for Advanced Research (CIFAR). The researchers intro­duced unsupervised learning procedures that could create layers of feature detectors without requiring labelled data. The objective in learning each layer of feature detectors was to be able to reconstruct or model the activities of feature detectors (or raw inputs) in the layer below. By ‘pre-training’ several layers of progressively more complex feature detectors using this reconstruction objective, the weights of a deep network could be initialized to sensible values. A final layer of output units could then be added to the top of the network and the whole deep system could be fine-tuned using standard backpropaga­tion. This worked remarkably well for recognizing handwritten digits or for detecting pedestrians, especially when the amount of labelled data was very limited.

2006年左右，由加拿大高階研究所（CIFAR）召集的一組研究人員重新喚起了人們對深度前饋式神經網路的興趣。研究人員引入了無監督的學習方法，這種方法可以在不需要帶標籤的數據的情況下建立特徵檢測器層。學習每一層特徵檢測器的目的是能夠重建或模擬下一層特徵檢測器（或原始輸入）的活動。通過使用該重構目標對多個逐步複雜的特徵檢測器進行「預訓練」，可以將深度網路的權值初始化爲合理值。最後一個輸出層可以新增到網路的頂部，整個深度系統可以使用標準反向傳播演算法進行微調。這對於識別手寫數位或檢測行人非常有效，尤其是在標籤數據量非常有限的情況下。

The first major application of this pre-training approach was in speech recognition, and it was made possible by the advent of fast graphics processing units (GPUs) that were convenient to program and allowed researchers to train networks 10 or 20 times faster. In 2009, the approach was used to map short temporal windows of coef­ficients extracted from a sound wave to a set of probabilities for the various fragments of speech that might be represented by the frame in the centre of the window. It achieved record-breaking results on a standard speech recognition benchmark that used a small vocabu­lary and was quickly developed to give record-breaking results on a large vocabulary task. By 2012, versions of the deep net from 2009 were being developed by many of the major speech groups and were already being deployed in Android phones. For smaller data sets, unsupervised pre-training helps to prevent overfitting, leading to significantly better generalization when the number of labelled exam­ples is small, or in a transfer setting where we have lots of examples for some ‘source’ tasks but very few for some ‘target’ tasks. Once deep learning had been rehabilitated, it turned out that the pre-training stage was only needed for small data sets.

這種預訓練方法的第一次主要應用出現在語音識別領域，便於程式設計並且能讓研究者以10倍到20倍的速度進行訓練的快速影象處理單元（GPUs）的出現讓這一切成爲可能。2009年，這個方法被用來獲得將從聲波中提取的短時間視窗對映爲不同的語音片段的概率。它用少量的發音樣本給出了創紀錄的語音識別結果，並且很快通過使用更多的發音樣本得到了發展。2009到2012年之間，深度網路經許多主要的語音識別團隊發展並被使用到了安卓手機中。對於更少的數據集，無監督的預訓練可以幫助減少過度擬合情況的發生，在數據數量很少或者有大量輸入樣本卻缺少目標樣本的情況下具有顯著更好的泛化概括能力。但深度學習恢復了名譽之後，事實證明其實只有數據集很小的情況下才需要預訓練階段。

There was, however, one particular type of deep, feedforward net­work that was much easier to train and generalized much better than networks with full connectivity between adjacent layers. This was the convolutional neural network (ConvNet). It achieved many practical successes during the period when neural networks were out of favour and it has recently been widely adopted by the computer-vision community.

然而，有一種特殊型別的深度前饋式神經網路比相鄰層之間完全連通的神經網路更容易訓練且泛化效能更好。這就是折積神經網路（ConvNet）。它在人們對神經網路失去興趣的時候取得了許多成功，如今被計算機視覺團隊廣泛採用。

Convolutional neural networks

ConvNets are designed to process data that come in the form of multiple arrays, for example a colour image composed of three 2D arrays containing pixel intensities in the three colour channels. Many data modalities are in the form of multiple arrays: 1D for signals and sequences, including language; 2D for images or audio spectrograms; and 3D for video or volumetric images. There are four key ideas behind ConvNets that take advantage of the properties of natural signals: local connections, shared weights, pooling and the use of many layers.

折積神經網路

折積神經網路被設計用於處理多維陣列數據，例如由三個包含了畫素值2D影象組成的具有三個顏色通道的彩色影象。許多數據形態都是以多維陣列的形式存在：1D用於信號和序列，包括語言；2D用於影象或音訊；3D用於視訊或有聲音的影象。折積神經網路利用了自然信號的特性，其背後有四個關鍵思想：區域性連線、權重共用、池化和多網路層的使用。

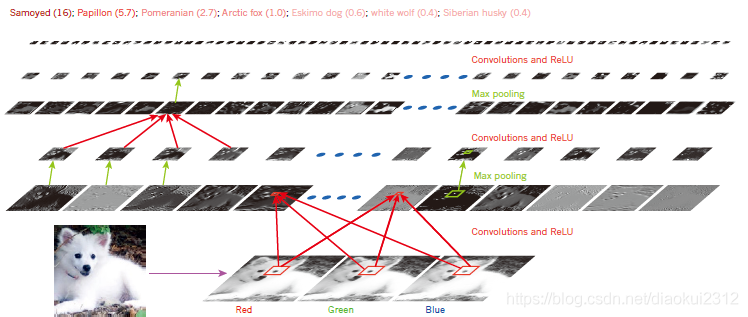
Figure 2 | Inside a convolutional network. The outputs (not the filters) of each layer (horizontally) of a typical convolutional network architecture applied to the image of a Samoyed dog (bottom left; and RGB (red, green, blue) inputs, bottom right). Each rectangular image is a feature map corresponding to the output for one of the learned features, detected at each of the image positions. Information flows bottom up, with lower-level features acting as oriented edge detectors, and a score is computed for each image class in output. ReLU, rectified linear unit.

圖2 折積神經網路內部

一個典型的折積網路結構的每一層（水平）的輸出（不是濾波器）應用於薩摩耶犬的影象（左下；RGB（紅、綠、藍）輸入，右下）。每個矩形影象是對應於在每個影象位置檢測到的學習特徵中的一個輸出的特徵對映。資訊流自下而上，低層特徵作爲定向邊緣檢測器，併爲輸出的每個影象類計算分數。ReLU，整流線性函數。

The architecture of a typical ConvNet (Fig. 2) is structured as a series of stages. The first few stages are composed of two types of layers: convolutional layers and pooling layers. Units in a convolu­tional layer are organized in feature maps, within which each unit is connected to local patches in the feature maps of the previous layer through a set of weights called a filter bank. The result of this local weighted sum is then passed through a non-linearity such as a ReLU. All units in a feature map share the same filter bank. Differ­ent feature maps in a layer use different filter banks. The reason for this architecture is twofold. First, in array data such as images, local groups of values are often highly correlated, forming distinctive local motifs that are easily detected. Second, the local statistics of images and other signals are invariant to location. In other words, if a motif can appear in one part of the image, it could appear anywhere, hence the idea of units at different locations sharing the same weights and detecting the same pattern in different parts of the array. Mathemati­cally, the filtering operation performed by a feature map is a discrete convolution, hence the name.

一個典型的折積神經網路由一系列階段組成（如圖2）。最初的幾個階段由兩種層次結構組成：折積層和池化層。折積層的單元被組織在不同特徵圖中，每個單元都通過過濾器形式的權重連線着前面層次的特徵圖的一小塊。隨後將該層的加權和輸入到如ReLU之類的非線性函數。同一個特徵圖中的每個單元都共用着同樣的過濾器形式的權重。每一層中不同的特徵圖使用不同的過濾器組。之所以設計成這樣有兩點原因：第一，在影象之類的陣列數據中，區域性的一組值通常高度相關，組成了特殊的且檢測方便的區域性圖案；第二，對影象或其它信號的區域性統計與其統計位置無關。換句話說，如果一個圖案能在一個部分出現，那它應該能在任何地方出現，因此不同部分的單元應當共用着同樣的權重並在陣列不同的部分檢測相同的模式。數學上來說，這種用特徵圖進行的過濾操作是一種離散折積，折積神經網路也因此得名。

Although the role of the convolutional layer is to detect local con­junctions of features from the previous layer, the role of the pooling layer is to merge semantically similar features into one. Because the relative positions of the features forming a motif can vary somewhat, reliably detecting the motif can be done by coarse-graining the posi­tion of each feature. A typical pooling unit computes the maximum of a local patch of units in one feature map (or in a few feature maps). Neighbouring pooling units take input from patches that are shifted by more than one row or column, thereby reducing the dimension of the representation and creating an invariance to small shifts and dis­tortions. Two or three stages of convolution, non-linearity and pool­ing are stacked, followed by more convolutional and fully-connected layers. Backpropagating gradients through a ConvNet is as simple as through a regular deep network, allowing all the weights in all the filter banks to be trained.

儘管折積層的作用是探測前一層特徵的區域性連線，但池化層的作用是將語意相似的特徵合併爲一個。因爲構成一個主題的特徵的相對位置可能會有所不同，所以可以通過粗粒化每個特徵的位置來可靠地探測到主題。一個典型的池化單元計算一個特徵圖（或幾個特徵圖）中一個的區域性塊的最大值。相鄰的池化單元從移動一行或一列的小塊獲取輸入數據，從而減少了表達的維數，並建立了對數據的不變性。兩個或三個階段的折積，非線性和池化，然後是更多的折積和完全連線層。通過折積神經網路的反向傳播演算法就像通過常規的深層網路一樣，允許訓練所有濾波器組中的所有權重。

Deep neural networks exploit the property that many natural sig­nals are compositional hierarchies, in which higher-level features are obtained by composing lower-level ones. In images, local combi­nations of edges form motifs, motifs assemble into parts, and parts form objects. Similar hierarchies exist in speech and text from sounds to phones, phonemes, syllables, words and sentences. The pooling allows representations to vary very little when elements in the previ­ous layer vary in position and appearance.

深度神經網路利用了許多自然信號都是分層次結構的特性，在這種結構中，高層次的特徵是通過合成較低層次的特徵來獲得的。在影象中，邊緣的區域性組合形成圖案，圖案組合成部分，部分形成物體。從電話中的聲音、音素、音節、單詞和句子，語音和文字中都存在類似的層次結構。當輸入數據前一層中的在位置和外觀上發生變化時，池化操作允許表示的變化很小。

The convolutional and pooling layers in ConvNets are directly inspired by the classic notions of simple cells and complex cells in visual neuroscience, and the overall architecture is reminiscent of the LGN–V1–V2–V4–IT hierarchy in the visual cortex ventral path­way. When ConvNet models and monkeys are shown the same pic­ture, the activations of high-level units in the ConvNet explains half of the variance of random sets of 160 neurons in the monkey’s infer­otemporal cortex. ConvNets have their roots in the neocognitron, the architecture of which was somewhat similar, but did not have an end-to-end supervised-learning algorithm such as backpropagation. A primitive 1D ConvNet called a time-delay neural net was used for the recognition of phonemes and simple words.

折積神經網路的折積層和池化層的概念靈感來源於神經科學中對簡單神經細胞和複雜神經細胞的經典觀念，它們的總體構架則讓人聯想到視覺腹側通路中的LGN–V1–V2–V4–IT層次結構。當同一幅影象被展示給折積神經網路模型和猴子的時候，折積網路中高層次單元的啓用過程達到了猴子下顳葉皮質中160個隨機神經元的變化的一半。折積神經網路受着神經認知學的影響，後者的架構和折積神經網路有點相似，但卻缺乏反向傳播這種端到端的有監督學習演算法。一種早期的被稱爲時延神經網路的一維折積神經網路曾被用來進行相似音素和單詞的識別。

There have been numerous applications of convolutional net­works going back to the early 1990s, starting with time-delay neu­ral networks for speech recognition and document reading. The document reading system used a ConvNet trained jointly with a probabilistic model that implemented language constraints. By the late 1990s this system was reading over 10% of all the cheques in the United States. A number of ConvNet-based optical character recog­nition and handwriting recognition systems were later deployed by Microsoft. ConvNets were also experimented with in the early 1990s for object detection in natural images, including faces and hands, and for face recognition.

早在20世紀90年代初，折積神經網路已經有了大量的應用，從語音識別和文件閱讀的時延神經網路開始。文件閱讀系統使用一個被訓練好的折積神經網路和一個概率模型，實現了語言方面的一些約束。到20世紀90年代末，這個系統被用來美國10%以上的支票閱讀上。微軟後來開發了許多基於折積神經網路的光學字元識別系統和手寫識別系統。在20世紀90年代早期折積神經網路也被用於自然影象中的目標檢測，包括臉和手，以及人臉識別。

Image understanding with deep convolutional networks

Since the early 2000s, ConvNets have been applied with great success to the detection, segmentation and recognition of objects and regions in images. These were all tasks in which labelled data was relatively abun­dant, such as traffic sign recognition, the segmentation of biological images particularly for connectomics, and the detection of faces, text, pedestrians and human bodies in natural images. A major recent practical success of ConvNets is face recognition.

基於深度折積網路的影象理解

自21世紀初以來，折積神經網路已成功地應用於影象中目標和區域的檢測、分割和識別。這些任務都是使用了大量的帶有標籤的數據，例如交通訊號識別、生物影象分割（尤其是連線組學）以及在自然影象中檢測臉部、文字、行人和人體。近年來，折積神經網路主要的成功應用是人臉識別。

Importantly, images can be labelled at the pixel level, which will have applications in technology, including autonomous mobile robots and self-driving cars. Companies such as Mobileye and NVIDIA are using such ConvNet-based methods in their upcoming vision sys­tems for cars. Other applications gaining importance involve natural language understanding and speech recognition.

重要的是，影象可以在畫素級別打標籤，這可以應用在諸如自主移動機器人和自動駕駛汽車等技術中。像Mobileye和NVIDIA這樣的公司正在把這種基於折積神經網路的方法用於他們即將推出的汽車視覺系統中。其他越來越重要的應用包括自然語言理解和語音識別。

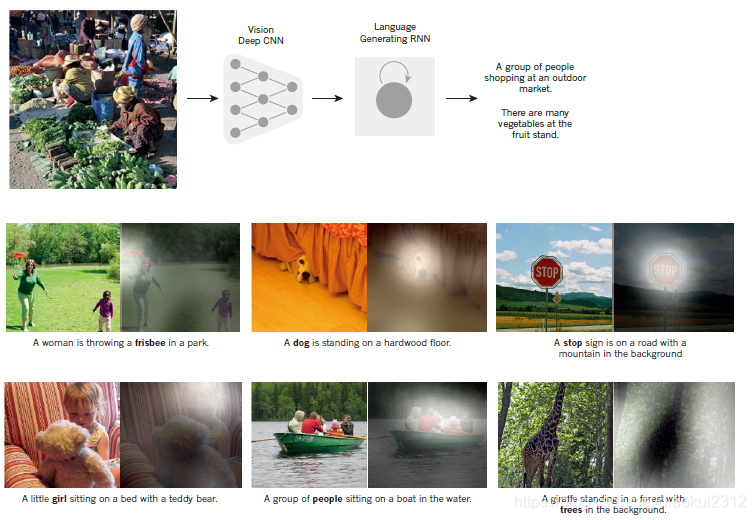
Figure 3 | From image to text.

Captions generated by a recurrent neural network (RNN) taking, as extra input, the representation extracted by a deep convolution neural network (CNN) from a test image, with the RNN trained to ‘translate’ high-level representations of images into captions (top). When the RNN is given the ability to focus its attention on a different location in the input image (middle and bottom; the lighter patches were given more attention) as it generates each word (bold), we found that it exploits this to achieve better ‘translation’ of images into captions.

圖3 從影象到文字

由遞回神經網路（RNN）生成的影象標題，作爲額外輸入數據，由深度折積神經網路（CNN）從測試影象中提取的特徵，並在RNN訓練下將影象的高階特徵「翻譯」爲影象標題（頂部）。當RNN在生成每個單詞（粗體）時，它能夠將注意力集中在輸入影象中的不同位置（中間和底部；較淺的塊被給予更多的關注），我們發現它利用這一點來更好地將影象「翻譯」成影象標題。

Despite these successes, ConvNets were largely forsaken by the mainstream computer-vision and machine-learning communities until the ImageNet competition in 2012. When deep convolutional networks were applied to a data set of about a million images from the web that contained 1,000 different classes, they achieved spec­tacular results, almost halving the error rates of the best compet­ing approaches1. This success came from the efficient use of GPUs, ReLUs, a new regularization technique called dropout, and tech­niques to generate more training examples by deforming the existing ones. This success has brought about a revolution in computer vision; ConvNets are now the dominant approach for almost all recognition and detection tasks and approach human performance on some tasks. A recent stunning demonstration combines ConvNets and recurrent net modules for the generation of image captions (Fig. 3).

儘管取得了這些成功，折積神經網路曾被主流計算機視覺界和機器學習界大規模拋棄，直到2012年的ImageNet比賽。當深度折積網路被應用在一個大概百萬張涵蓋了一千種不同類別的網路影象的數據集上時，它得到了引入注目的結果：它的誤差率只有當時比賽中競爭者的一半！這次成功有來自GPU、ReLU、一種被稱爲dropout的全新正則技術和通過扭曲變換現有樣本來生成更多訓練樣本等技術的貢獻。這項成功爲計算機視覺界帶來了一場革命。折積神經網路現在成爲了幾乎所有識別和檢測專案的主要方法，並且在某些任務上達到了人類的識別水平。最近一個令人震驚的例子是結合折積神經網路和回圈神經網路（遞回網路）模型來生成影象標題。

Recent ConvNet architectures have 10 to 20 layers of ReLUs, hun­dreds of millions of weights, and billions of connections between units. Whereas training such large networks could have taken weeks only two years ago, progress in hardware, software and algorithm parallelization have reduced training times to a few hours.

最近的折積神經網路架構有10到20層採用了ReLUs函數、成千上萬個權重、幾十億個連線。兩年前，訓練如此龐大的網路只需要幾周時間，但在硬體、軟體和演算法並行化的進步已將訓練時間縮短到幾個小時。

The performance of ConvNet-based vision systems has caused most major technology companies, including Google, Facebook, Microsoft, IBM, Yahoo!, Twitter and Adobe, as well as a quickly growing number of start-ups to initiate research and development projects and to deploy ConvNet-based image understanding products and services.

基於折積神經網路的視覺系統的效能已經引起了大多數大型技術公司的關注，包括Google、Facebook、Microsoft、IBM、Yahoo！推特和Adobe，以及數量迅速增長的初創企業，它們發起研發專案，開發基於折積神經網路的影象理解產品和服務。

ConvNets are easily amenable to efficient hardware implemen­tations in chips or field-programmable gate arrays. A number of companies such as NVIDIA, Mobileye, Intel, Qualcomm and Samsung are developing ConvNet chips to enable real-time vision applications in smartphones, cameras, robots and self-driving cars.

折積神經網路很容易在晶片或現場可程式化門陣列中有效的實現。許多公司，如NVIDIA、Mobileye、Intel、Qualcomm和Samsung正在開發折積神經網路晶片，以便在智慧手機、相機、機器人和自動駕駛汽車中實現實時視覺應用。

Distributed representations and language processing

Deep-learning theory shows that deep nets have two different expo­nential advantages over classic learning algorithms that do not use distributed representations. Both of these advantages arise from the power of composition and depend on the underlying data-generating distribution having an appropriate componential structure. First, learning distributed representations enable generalization to new combinations of the values of learned features beyond those seen during training (for example, 2n combinations are possible with n binary features). Second, composing layers of representation in a deep net brings the potential for another exponential advantage(exponential in the depth).

分佈式特徵表示和語言處理

深度學習理論表明，與不使用分佈式特徵表示的經典學習演算法相比，深度網路具有兩種不同的巨大的優勢。這兩個優點都源於組合的能力，並依賴於具有適當元件結構的底層數據生成分佈。首先，學習分佈式特徵表示可以泛化到新學習特徵值的組合，而不是訓練期間看到的那些值（例如，對於n個二進制特徵，2n個可能的組合）。第二，在一個深度網路中組合表示層帶來了另一個巨大的優勢潛力（指數級的深度）。

The hidden layers of a multilayer neural network learn to repre­sent the network’s inputs in a way that makes it easy to predict the target outputs. This is nicely demonstrated by training a multilayer neural network to predict the next word in a sequence from a local context of earlier words. Each word in the context is presented to the network as a one-of-N vector, that is, one component has a value of 1 and the rest are 0. In the first layer, each word creates a different pattern of activations, or word vectors (Fig. 4). In a language model, the other layers of the network learn to convert the input word vec­tors into an output word vector for the predicted next word, which can be used to predict the probability for any word in the vocabulary to appear as the next word. The network learns word vectors that contain many active components each of which can be interpreted as a separate feature of the word, as was first demonstrated in the context of learning distributed representations for symbols. These semantic features were not explicitly present in the input. They were discovered by the learning procedure as a good way of factorizing the structured relationships between the input and output symbols into multiple ‘micro-rules’. Learning word vectors turned out to also work very well when the word sequences come from a large corpus of real text and the individual micro-rules are unreliable. When trained to predict the next word in a news story, for example, the learned word vectors for Tuesday and Wednesday are very similar, as are the word vectors for Sweden and Norway. Such representations are called distributed representations because their elements (the features) are not mutually exclusive and their many configurations correspond to the variations seen in the observed data. These word vectors are composed of learned features that were not determined ahead of time by experts, but automatically discovered by the neural network. Vector representations of words learned from text are now very widely used in natural language applications.

一個多層神經網路的隱藏層學習如何描述網路的輸入來使預測目標輸出更容易。一個很好的例子是，通過訓練多層次神經網路來利用本地文字中已有的單詞預測下一個單詞（譯註：此句參照Advances in Neural Information Processing Systems ）。上下文的每個單詞都以「N分之1向量」表示，也就是隻有一個位置的值爲1其餘位置值皆爲0的向量。在第一層，每個單詞建立出不同的單詞向量（如圖4）。在一個語言模型中，網路的其他層學習如何將輸入的單詞向量轉化爲作爲輸出的預測單詞向量，以此來預測詞彙表中每一個單詞成爲下一個單詞的可能性。網路通過許多啓用元件學習單詞向量，每個啓用元件都可以理解爲單詞的一個特徵分量，就像我們之前用分佈式特徵進行學習那部分那樣。這些（分佈式的）語意結構沒有被明確地表現在輸入中，而是由學習流程發現出來的，這是一種將輸入和輸出間結構化關係分解爲多個「微規則」的好方式。學習單詞向量的方法被發現在單詞集來自於真實文字和個別微規則不可靠時也表現得非常好。當它被訓練用來預測新聞中的下一個詞的時候，如「星期二」與「星期四」、「瑞典」與「挪威」之類的單詞之間的單詞向量可能非常相似。這樣的特徵被稱爲分佈式特徵是因爲它們的特徵並不互斥並且它們的許多設定資訊與觀測到的數據變化一致。這些單詞向量由神經網路自動學習到的特徵組合而成而非由專家事先定義。從文字中學習單詞的向量特徵的方法如今已被廣泛應用於自然語言的應用中。

The issue of representation lies at the heart of the debate between the logic-inspired and the neural-network-inspired paradigms for cognition. In the logic-inspired paradigm, an instance of a symbol is something for which the only property is that it is either identical or non-identical to other symbol instances. It has no internal structure that is relevant to its use; and to reason with symbols, they must be bound to the variables in judiciously chosen rules of inference. By contrast, neural networks just use big activity vectors, big weight matrices and scalar non-linearities to perform the type of fast ‘intui­tive’ inference that underpins effortless commonsense reasoning.

「特徵描述」處於邏輯啓發(logic-inspired)和神經網路啓發(neural-network-inspired)的探討爭論的中心。在邏輯啓發的觀點中，一個符號的範例應該是一個既不能被其它符號範例定義也不能無法被其它符號範例定義的東西（譯註：雖然初讀很矛盾，但想想好像有道理）。它不應該有和它的使用相關的更內部的結構。而在符號語意上，它必須和推理規則中的變化嚴格對應。相比之下，神經網路只是使用大型的啓用向量、很多權重矩陣和標量非線性化來表現出支援常識推理的「直覺」推斷。

Before the introduction of neural language models, the standard approach to statistical modelling of language did not exploit distrib­uted representations: it was based on counting frequencies of occur­rences of short symbol sequences of length up to N (called N-grams). The number of possible N-grams is on the order of VN, where V is the vocabulary size, so taking into account a context of more than a handful of words would require very large training corpora. N-grams treat each word as an atomic unit, so they cannot generalize across semantically related sequences of words, whereas neural language models can because they associate each word with a vector of real valued features, and semantically related words end up close to each other in that vector space (Fig. 4).

在介紹神經語言模型之前，解釋下標準方法，語言統計建模的標準方法並沒有利用分佈式特徵表示：它是基於長度爲N的短符號序列（稱爲N-圖）出現頻率的計數。可能的N-gram的數位接近於VN，其中V是詞彙量的大小，考慮到一個包含多個單詞的上下文將需要非常大的訓練語料庫。N-gram將每個單詞作爲一個原子單元來處理，因此它們不能在語意相關的單詞序列中一概而論，而神經語言模型可以，因爲它們將每個單詞與實值特徵向量相關聯，並且語意相關的單詞在該向量空間中彼此接近（圖4）。

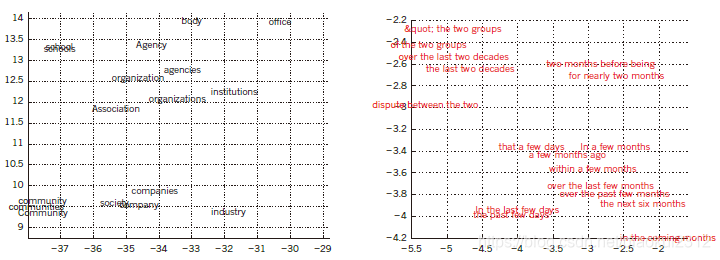
Figure 4 | Visualizing the learned word vectors.

On the left is an illustration of word representations learned for modelling language, non-linearly projected to 2D for visualization using the t-SNE algorithm. On the right is a 2D representation of phrases learned by an English-to-French encoder–decoder recurrent neural network. One can observe that semantically similar words or sequences of words are mapped to nearby representations. The distributed representations of words are obtained by using backpropagation to jointly learn a representation for each word and a function that predicts a target quantity such as the next word in a sequence (for language modelling) or a whole sequence of translated words (for machine translation).

圖4單詞向量學習視覺化。

左邊是一個爲建模語言學習的單詞表示的說明，使用t-SNE演算法將其非線性投影到2D以進行視覺化。 右側是英語到法語編碼器-解碼器遞回神經網路學習的短語的二維表示。 可以看到，語意相似的單詞或句子已對映到附近的特徵表示形式。通過使用反向傳播演算法共同學習每個單詞的特徵表示以及預測目標數量的函數（例如句子中的下一個單詞（用於語言建模）或翻譯單詞的整個句子（用於機器翻譯）），可以獲得單詞的分佈式特徵表示形式。

Recurrent neural networks

When backpropagation was first introduced, its most exciting use was for training recurrent neural networks (RNNs). For tasks that involve sequential inputs, such as speech and language, it is often better to use RNNs (Fig. 5). RNNs process an input sequence one element at a time, maintaining in their hidden units a ‘state vector’ that implicitly contains information about the history of all the past elements of the sequence. When we consider the outputs of the hidden units at different discrete time steps as if they were the outputs of different neurons in a deep multilayer network (Fig. 5, right), it becomes clear how we can apply backpropagation to train RNNs.

遞回神經網路

當反向傳播演算法首次被引入時，它最令人興奮的用途是訓練遞回神經網路（RNNs）。對於涉及序列輸入的任務，例如語音和語言，使用RNNs更好（圖5）。RNNs一次只處理一個輸入序列的元素，在它們的隱單元中維護一個「狀態向量」，它隱含地包含序列元素過去的歷史資訊。當我們考慮隱單元在不同離散時間步長的輸出，就好像它們是深度多層網路中不同神經元的輸出一樣（圖5，右圖），我們就可以清楚地知道如何應用反向傳播來訓練RNNs。

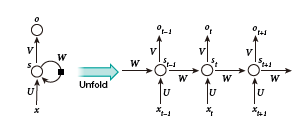
Figure 5 | A recurrent neural network and the unfolding in time of the computation involved in its forward computation.

The artificial neurons (for example, hidden units grouped under node s with values st at time t) get inputs from other neurons at previous time steps (this is represented with the black square, representing a delay of one time step, on the left). In this way, a recurrent neural network can map an input sequence with elements $x_t$ into an output sequence with elements $o_t$, with each $o_t$ depending on all the previous $x_t'$ (for $t'\le t$). The same parameters (matrices U,V,W ) are used at each time step. Many other architectures are possible, including a variant in which the network can generate a sequence of outputs (for example, words), each of which is used as inputs for the next time step. The backpropagation algorithm (Fig. 1) can be directly applied to the computational graph of the unfolded network on the right, to compute the derivative of a total error (for example, the log-probability of generating the right sequence of outputs) with respect to all the states st and all the parameters.

圖5 遞回神經網路及其正向計算所涉及的計算時間展開。

人工神經元（例如，在節點s下分組的隱單元，在時間t處的值爲st）在之前的時間步長（左側用黑色正方形表示，表示一個時間步長的延遲）從其他神經元獲得輸入數據。這樣，一個遞回神經網路就可以把一個含有$x_t$的輸入序列對映成一個含有$o_t$的輸出序列，每個$o_t$依賴於先前的$x_t'$（對於$t'\le t$）。每個時間步長使用相同的參數（矩陣U、V、W）。許多其他的架構是可能的，包括網路生成的一系列輸出數據（例如,字），每個輸出數據被用作下一個時間步長的輸入數據。反向傳播演算法（圖1）可直接應用於右側展開網路的計算圖，以計算關於所有狀態st和所有參數的總誤差（例如，生成正確輸出序列的對數概率）的導數。

RNNs are very powerful dynamic systems, but training them has proved to be problematic because the backpropagated gradients either grow or shrink at each time step, so over many time steps they typically explode or vanish.

RNNs是非常強大的動態系統，但是訓練它們被證明是有問題的，因爲反向傳播的梯度在每一個時間步長都會增長或下降，因此在許多時間步長中，它們通常會激增或降爲0。

Thanks to advances in their architecture and ways of training them, RNNs have been found to be very good at predicting the next character in the text or the next word in a sequence, but they can also be used for more complex tasks. For example, after reading an English sentence one word at a time, an English ‘encoder’ network can be trained so that the final state vector of its hidden units is a good representation of the thought expressed by the sentence. This thought vector can then be used as the initial hidden state of (or as extra input to) a jointly trained French ‘decoder’ network, which outputs a prob­ability distribution for the first word of the French translation. If a particular first word is chosen from this distribution and provided as input to the decoder network it will then output a probability dis­tribution for the second word of the translation and so on until a full stop is chosen. Overall, this process generates sequences of French words according to a probability distribution that depends on the English sentence. This rather naive way of performing machine translation has quickly become competitive with the state-of-the-art, and this raises serious doubts about whether understanding a sen­tence requires anything like the internal symbolic expressions that are manipulated by using inference rules. It is more compatible with the view that everyday reasoning involves many simultaneous analogies that each contribute plausibility to a conclusion.

得益於它們結構和訓練方式的改進，人們發現回圈神經網路非常擅長預測文字中的下一個字母或者序列中的下一個單詞，但它們也可以用來完成更復雜的任務。比如，一個一個單詞地閱讀完一句英語之後，一個英語的「編碼器」網路就可以被訓練，其內部隱藏層的狀態向量將能很好地表徵這句話表達的意思。這個表徵句子含義的向量隨後可以被用來作爲另一個連帶被訓練的法語「解碼器」的隱藏層的初始值（或者是作爲其外界的額外輸入），這次輸入對應的輸出是翻譯成的法語句子裡第一個單詞的概率分佈。如果該分佈中的某首單詞被選擇作爲「解碼器」網路的第二次輸入，它又會經網路給出句子中第二個單詞的概率分佈，這一過程不斷重複直到句號爲止。這個過程概括來說就是根據英語句子決定的概率分佈來生成法語單詞序列。這個有點稚拙的機器翻譯方法迅速地成爲了頂尖翻譯方法的競爭者，而這也帶來了一個嚴肅的疑問：理解一個句子是否需要任何由推理規則操縱的內部特徵？這種方法更符合這樣一種觀點：日常的推理中包含着許多同時發生的類比，而每次類比都增加了所得出結論的可信度

Instead of translating the meaning of a French sentence into an English sentence, one can learn to ‘translate’ the meaning of an image into an English sentence (Fig. 3). The encoder here is a deep Con­vNet that converts the pixels into an activity vector in its last hidden layer. The decoder is an RNN similar to the ones used for machine translation and neural language modelling. There has been a surge of interest in such systems recently.

類比把法語句子的意思翻譯成英語句子，人們可以學習把影象的意思「翻譯」成英語句子（圖3）。這裏的編碼器是一個可以在最後一個隱層將畫素轉換成活動向量的深度折積網路。譯碼器是一個類似於機器翻譯和神經網路語言模型的RNNs。最近人們對這類系統的興趣激增。

RNNs, once unfolded in time (Fig. 5), can be seen as very deep feedforward networks in which all the layers share the same weights. Although their main purpose is to learn long-term dependencies, theoretical and empirical evidence shows that it is difficult to learn to store information for very long.

RNNs一旦在時間上展開（圖5），就可以看作是一個所有層共用相同的權重的深度前饋神經網路。雖然他們的主要目的是學習長期依賴性，但理論和經驗證據表明，學習長期儲存資訊是很困難的。

To correct for that, one idea is to augment the network with an explicit memory. The first proposal of this kind is the long short-term memory (LSTM) networks that use special hidden units, the natural behaviour of which is to remember inputs for a long time. A special unit called the memory cell acts like an accumulator or a gated leaky neuron: it has a connection to itself at the next time step that has a weight of one, so it copies its own real-valued state and accumulates the external signal, but this self-connection is multiplicatively gated by another unit that learns to decide when to clear the content of the memory.

爲了糾解決這個問題，一個想法是擴充網路儲存。第一種建議是使用特殊隱單元的LSTM，其自然行爲是長期儲存輸入。一個叫做記憶細胞的特殊單元就像一個累加器或一個門控神經元：它在下一個時間步長有一個權重連線到它自己，複製它自己狀態的真實值並累積外部信號，但是這個自聯接被另一個單元學習決定何時清除記憶體的內容乘法門控制的。

LSTM networks have subsequently proved to be more effective than conventional RNNs, especially when they have several layers for each time step87, enabling an entire speech recognition system that goes all the way from acoustics to the sequence of characters in the transcription. LSTM networks or related forms of gated units are also currently used for the encoder and decoder networks that perform so well at machine translation.

LSTM網路後來被證明比傳統的RNNs更有效，尤其是當它們在每個時間步長有多個層時，整個語音識別系統能夠實現從聲學轉錄爲字元序列。LSTM網路或相關形式的門控單元目前也用於編碼器和解碼器網路，在機器翻譯方面表現得非常好。

Over the past year, several authors have made different proposals to augment RNNs with a memory module. Proposals include the Neural Turing Machine in which the network is augmented by a ‘tape-like’ memory that the RNN can choose to read from or write to, and memory networks, in which a regular network is augmented by a kind of associative memory. Memory networks have yielded excel­lent performance on standard question-answering benchmarks. The memory is used to remember the story about which the network is later asked to answer questions.

在過去的幾年裡，幾位學者提出了不同的建議用於來擴充RNNs記憶體模組。建議包括神經圖靈機，其中網路可以由RNNs選擇讀或寫的「磁帶狀」記憶體擴充，而記憶網路中的常規網路由聯想記憶體擴充。記憶網路在標準問答基準測試中表現出色。記憶是用來記住隨後被要求回答問題的範例。

Beyond simple memorization, neural Turing machines and mem­ory networks are being used for tasks that would normally require reasoning and symbol manipulation. Neural Turing machines can be taught ‘algorithms’. Among other things, they can learn to output a sorted list of symbols when their input consists of an unsorted sequence in which each symbol is accompanied by a real value that indicates its priority in the list. Memory networks can be trained to keep track of the state of the world in a setting similar to a text adventure game and after reading a story, they can answer questions that require complex inference. In one test example, the network is shown a 15-sentence version of the The Lord of the Rings and correctly answers questions such as 「where is Frodo now?」.

除了簡單的記憶化，神經圖靈機和記憶網路被用於通常需要推理和符號操作的任務。還可以教神經圖靈機 「演算法」。除此之外，當他們的輸入由一個未排序的符號序列組成時，他們可以學習輸出一個經過排序的符號序列，在這個序列中，每個符號都有一個與其在列表中對應的表面優先順序的真實值。記憶網路可以訓練成追蹤一個設定類似文字冒險遊戲的世界的狀態，在閱讀故事之後，他們可以回答需要複雜推理的問題。在一個測試例子中，網路可以正確回答15句版的《指環王》諸如「Frodo現在在哪裏？」的問題。

The future of deep learning

Unsupervised learning had a catalytic effect in reviving interest in deep learning, but has since been overshadowed by the successes of purely supervised learning. Although we have not focused on it in this Review, we expect unsupervised learning to become far more important in the longer term. Human and animal learning is largely unsupervised: we discover the structure of the world by observing it, not by being told the name of every object.

深度學習的未來展望

無監督學習在恢復對深度學習的興趣方面起到了催化作用，但自那以後，純粹的監督學習的成功使其黯然失色。雖然我們在這篇論述中沒有關注它，但我們期望無監督學習在長期內會變得更加重要。人類和動物的學習在很大程度上是不受監督的：我們通過觀察發現世界的結構，而不是被告知每一個事物的名稱。

Human vision is an active process that sequentially samples the optic array in an intelligent, task-specific way using a small, high-resolution fovea with a large, low-resolution surround. We expect much of the future progress in vision to come from systems that are trained end-to-end and combine ConvNets with RNNs that use reinforcement learning to decide where to look. Systems combining deep learning and rein­forcement learning are in their infancy, but they already outperform passive vision systems at classification tasks and produce impressive results in learning to play many different video games.

人類視覺是一個活躍的過程，它使用一個小的、高解析度的視網膜中央窩和一個大的、低解析度的環繞物，以智慧的、特定的方式對光線進行採樣。我們期望未來在機器視覺方面經過端到端訓練的系統有更大的進步，，並將ConvNets與RNNs相結合，使用強化學習來決定走向。將深度學習和強化學習相結合的系統還處於初級階段，但它們在分類任務上的表現已經超過了被動視覺系統，並在學習操作多種不同的視訊遊戲方面取得了令人印象深刻的成果。

Natural language understanding is another area in which deep learn­ing is poised to make a large impact over the next few years. We expect systems that use RNNs to understand sentences or whole documents will become much better when they learn strategies for selectively attending to one part at a time.

自然語言理解將是深度學習在未來幾年產生重大影響的另一個領域。我們希望使用RNNs理解句子或整個文件的系統在學習每次選擇性地關注一部分內容的策略時會變得更好。

Ultimately, major progress in artificial intelligence will come about through systems that combine representation learning with complex reasoning. Although deep learning and simple reasoning have been used for speech and handwriting recognition for a long time, new paradigms are needed to replace rule-based manipulation of symbolic expressions by operations on large vectors.

最終，人工智慧的重大進展將來自將特徵表示學習與複雜推理相結合的系統。雖然在語音和手寫體識別中使用深度學習和簡單推理已經有很長一段時間了，但是仍需要通過操作大量向量的新範式來取代基於規則的字元表達式操作。