假設空間

​ 在周志華老師的《機器學習》一書中提到，模型的訓練就是利用訓練數據在數據屬性構成的「假設空間」中進行搜尋，在搜尋過程中會刪除假設空間的某些假設，最終留下一些假設形成「版本空間」，最終再通過這個模型進行推理。

​ 至於什麼是假設空間，假設的刪除是怎麼生成的，搬運一篇部落格，講的非常清楚：

效能評價

​ 機器學習演算法是想通過已有的數據來構建模型進行預測，預測的是好是壞，我們需要對演算法進行評估。

​ 實際上我理解這種評估就和我們日常參加考試是一個道理：日常我們做的習題是訓練我們的考試能力，我們稱之爲「訓練集」；那麼考試題目就是測試我們被訓練的怎麼樣，稱之爲「測試集」。畢業之後，是否能根據訓練和測試的數據進行舉一反三，解決實際問題，就看我們自己這個「模型」的泛化能力了。
那麼選擇哪些題做平時的習題，哪些做考題呢？這個是提高我們考試能力和解決問題能力的一個關鍵。全部挑容易的做習題，考試考不過。全部挑難的，又會失去一般性。
​ 學習演算法和這個類似，如何挑選樣本作爲訓練集和測試集，一般有幾種方法。和選習題不一樣的是，習題一般來說還是選擇一些會考的原題，讓考生們心裏有點信心；而演算法訓練的話，一般是會保證訓練集和測試集無交集。

​ 那麼我們怎麼去劃分樣本對學習演算法進行評估呢，一般來說有以下3中評估方法：

• 留出法
• 交叉驗證法
• 自助法

​ 介紹完評估方法後，我們看一下用哪些指標來量化一個評估方法的好壞。

評估方法

留出法

​ 留出法就是將整個數據樣本集按照某種原則直接分成s和t兩個集合。這個原則有以下幾點考慮：

• 分層採樣。比如數據樣本是一個二分類問題，那麼儘量保證測試集中的正例/反例的比例與數據樣本的整體比例相同。測試集相同了訓練集自然也相同。比如總共1000個樣本，700個正例，300個反例。假設訓練集選擇700個樣例，如果全部把正例放進去，泛化能力肯定不行，保證490個正例在訓練集，210個在測試集中會效果比較好。
• 一次劃分往往無法準確的評估，需要按同一個原則劃分n次，然後進行n次評估後求平均值。某個樣本（xi，yi）在n次劃分中會反覆 反復出現在訓練集和測試集中。
• 常見的劃分爲2/3 - 4/5爲訓練集，其餘的爲測試集。訓練集太大，導致測試集小無法準確評估，若訓練集太小則直接無法擬合全域性狀態。

交叉驗證法

​ 交叉驗證法我理解是留出法的一種具體操作方式，就是將整個數據樣本劃分成k個集合，用其中k-1個集合的並集作爲訓練集，另外的一個作爲測試集。從k = 1一直到k = k，每個集合都會成爲一次測試集。總共做k次評估，求平均值。
​ 此時，k的取值是比較關鍵的參數，演算法中的調參指的就是調整這種參數。參數不同，演算法的效能會出現比較大的變化。

自助法

​ 假設一個m個樣本的數據樣本集d，從整體樣本中隨機挑選一個樣本放入到訓練集d-中，挑選完的樣本繼續留在原集閤中。這樣挑選m次來形成訓練集。

• 訓練集大小和已知數據集大小相同，但是訓練集中有重複的數據，還有約0.368 * m的數據不會出現在訓練集中，這個數位大家可以去看一下《機器學習》這本書。
• 訓練集採用隨機的方式選擇樣本，會改變原樣本的分佈情況，會產生一些偏差，適用於樣本量較小的情況。

效能度量

錯誤率與精度

​ 錯誤率比較好理解，對於$m$個測試樣本的測試機，如果有$e$個樣本分類錯誤，那麼錯誤率就是$E = e/m$。

​ 精度就是$acc = 1-E$

​ 光有錯誤率和精度是無法全面的評價一個學習演算法的。

查準率 & 查全率

​ 查準率的含義就是我預測出來的結果又多少是對的。

​ 查全率的含義就是我預測出來的結果是不是全的。

​ 從簡單的問題看起，針對二分類問題，我們可以將最終預測的結果分成4個部分，大家仔細捋一捋，容易亂：

• 真正例(True Positive)，TP。演算法找到的，符合要求的樣本。
• 假正例(False Positive)，FP。演算法找到的，但是不符合要求的樣本。
• 真反例(True Negative)，TN。演算法找到的，但是實際不符合要求的樣本。
• 假反例(False Negative)，FN。演算法沒找到的，但是是符合要求的樣本。

​ 這裏有一個概念可以引入：混淆矩陣。混淆矩陣就是一個$n * n， n = 類別數$的矩陣，混淆矩陣的每一列代表了預測類別，每一列的總數表示預測爲該類別的數據的數目；每一行代表了數據的真實歸屬類別，每一行的數據總數表示該類別的數據範例的數目。

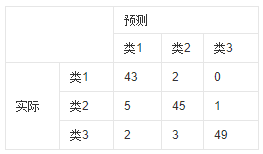
​ 我們具體來他討論二分類問題，那就是正例(符合要求)和反例(不符合要求)兩種。

​ 查準率就是說根據模型找出來的樣本中，真正符合要求的有多少，畢竟有找錯的(假正例)。所以查準率的計算方式爲：
$P = \frac{TP}{TP+FP}$
​ 查全率則是指根據模型找出來的樣本中，符合要求的樣本佔全部符合要求的樣本的比例，畢竟有漏掉的(假反例，就是演算法判斷這個樣本不是符合要求的，實際上是符合要求的樣本)。那麼查全率的計算方式爲：
$R=\frac{TP}{TP+FN}$
​ 查全率和查準率是相互制約的兩個效能指標，查準率高意味着會把一些沒那麼有把握的樣本排除掉(上一篇文章提到的，生成式模型會計算概率，根據概率和閾值進行分類，查準率提高的話就表示這個閾值定的比較高)，那麼可能就會把一些樣本漏掉成爲假反例，導致查全率降低。如果儘可能的把結果查全，表示這個閾值定的比較低，就會產生一些假正例，從而降低查準率。

​ 那麼一個演算法來了，怎麼平衡的，根據什麼樣的指導原則來選擇呢？這就引出了P-R圖和ROC圖。

P-R圖

​ P-R圖的思路是，把演算法模型給出的預測結果以樣本爲單位按概率高低進行排序，可能性最高的排最前面，最不可能的放最後面。然後按此順序逐個把樣本作爲正例進行預測，再計算查全率與差準率$(R,P)$，把一系列的$(R,P)$點標記在以查全率爲橫軸、查準率爲縱軸的座標裡。

​ 參考《機器學習》中的圖：

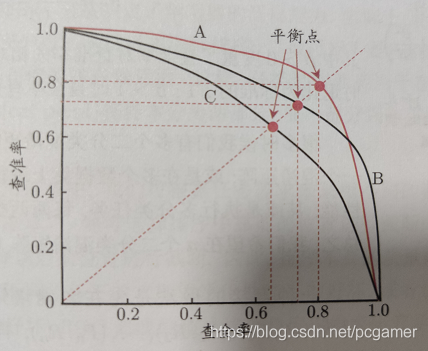
​ 可以看出，隨着查全率增加，查準率是下降的。

• 當P = R時，此時是比較平衡的策略
• 考察A/C兩條曲線，A曲線的任何一個點的P, R都比C曲線的值要高，說明A曲線代表的演算法完勝C曲線代表的演算法
• 但是大部分情況是A/B兩條曲線所描述的，在A/B兩條曲線的交點右側，在查準率相同的情況下，B曲線的查全率更優秀；在交點左邊，在查全率相同的情況下，A曲線的查準率更優秀，所以就需要根據具體情況具體分析了。
• 如果非要綜合比較，那麼就是計算曲線與兩根軸圍住的區域面積，誰大誰的綜合效能就更強。

​ 那麼怎麼生成這個曲線呢，我們來舉個栗子：

​ 假設預測了十個樣本，樣本的概率如下，其中3號、5號、8號樣本爲反例：

1	2	3	4	5	6	7	8	9	10
0.95	0.9	0.85	0.8	0.75	0.7	0.65	0.6	0.55	0.5

1. 生成第一個點：把1號樣本拿出來做正例，那麼此時TP = 1，FP = 0，FN = 6（2,4,6,7,9,10均爲假反例）。計算得出查準率P = 100%。而查全率只有1/7。

2. 生成第二個點：把1號2號樣本都作爲正例，此時TP = 2，FP = 0，FN=5。計算得出查準率P = 100%。查全率爲1/6。

3. 生成第三個點：TP = 2，FP = 1，FN=5。計算得出查準率P = 2/3。查全率爲2/7。

   …

4. 最後一個點：把所有的樣本都算作正例，TP = 7， FP = 3，FN = 0。計算得出查準率P = 70%(最低)，查全率爲100%(最高)。

​ 這個圖就不畫了，沒有上面的圖能說明問題。

ROC & AUC

​ 對於二分類問題，ROC圖還是通過TP/FP/TN/FN四個值來做計算，不過橫軸換成假正例(FPR, False Positive Rate)，縱軸是真正例率(TPR, True Positive Rate)。
$TPR = \frac{TP}{TP+FN}$

$FPR = \frac{FP}{TN+FP}$

​ 通過這個計算公式，我們可以來理解一下這種統計方式的思想：

• TPR是想發現演算法漏了哪一些樣本，也就是被演算法漏掉的、實際上是符合條件的那部分樣本(FN)。如果是故障診斷演算法的話，就是說演算法判斷是有故障的可行度有多高，也可以稱之爲真陽率。
• FPR是想發現演算法錯判斷成符合條件的樣本佔整個不符合條件樣本中的比例。如果是故障診斷演算法的話，就是說演算法認爲是故障的話，實際上不是故障的概率有多大，稱之爲假陽率。

​ 畫ROC圖的方式和P-R圖的方式一樣的，只是每次計算的值不一樣而已，就不再舉個栗子了。

​ 直接把圖扔出來：

[外連圖片轉存失敗,源站可能有防盜鏈機制 機製,建議將圖片儲存下來直接上傳(img-LT5LTD8s-1597055079908)(C:%5CUsers%5CZL%5CAppData%5CRoaming%5CTypora%5Ctypora-user-images%5Cimage-20200806163141212.png)]

• 隨着越來越多的樣本加入到正例裡，TPR會逐步增高，最理想的狀況就是從原點順着縱軸直接上去，也就是FPR持續爲0。然後隨着低概率的事件加入到正例裡，順着TPR=1.0的橫軸達到右上角，也就是TPR一直爲1。

• 而圖中的Bad Model Line表示隨着樣本的逐步增加，TPR=FPR，也就是隨機猜測，就是扔硬幣，你的預測準確率只有50%一樣。

• 一般來說，真實的曲線位於剛纔說的兩者之間，就像圖中的黑色線。

• 曲線中最好的分界線(也就是閾值從哪個位置(哪個樣本處，因爲樣本是按照順序來構造這條ROC圖))就是曲線的斜率小於45度的時候。因爲從這個點開始，TPR增加率就開始低於FPR的增加率了。爲了增加更多的TPR，需要增加更多額FPR作爲代價。

AUC表示曲線下面 下麪覆蓋的面積，可以表示這個演算法的綜合效能。

ROC和P-R圖從不同的評價方向來評價一個演算法的好壞，舉一個極端的例子：一個二類分類問題一共10個樣本，其中9個樣本爲正例，1個樣本爲負例，在全部判正的情況下準確率將高達90%，而這並不是我們希望的結果，尤其是在這個負例樣本得分還是最高的情況下，模型的效能本應極差，從準確率上看卻適得其反。而AUC能很好描述模型整體效能的高低。這種情況下，模型的AUC值將等於0，因爲第一個點計算出來的TPR = 0，而FPR = 1，已經是最右邊的那個點了。

代價敏感錯誤與代價曲線

​ 在一些情況下，P-R圖/ROC也沒法很客觀的評價一個學習演算法。比如醫療相關的學習期，判斷病人是否有某種疾病。FP的情況，也就是沒病的誤判成有病的情況，這種情況下，最多就是浪費病人的時間和金錢，重新做了一些檢查。但是如果是FN的情況，也就是有病的判斷成沒病，這種情況就會耽誤最佳治療時間，最終可能導致生命危險。很明顯，FP和FN的代價是不一樣的，而P-R圖和ROC圖中沒有對這個的評價。

​ 爲了把判斷錯誤的代價考慮到效能度量裡，我們可以把上面提到的混淆矩陣改造一下，矩陣中的數位是用於描述錯誤代價：

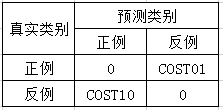
​ 針對這個矩陣，定義了座標的橫軸與縱軸：

​ 橫軸：
$P(+)cost=\frac{p*cost_{01}}{p*cost_{01}+(1-p)cost_{10}} ①$
​ $p$是表示樣本中正例的概率，拿ROC中的那個例子來說，$p=0.7$

​ 所以這個公式本質上可以看成就是正例的概率$p$本身，比如在沒有代價的計算中，$cost_{01} = cost_(10)$，那麼這個公式就退化成$P(+)cost = p$。假設正例被判斷成反例的後果更嚴重一點，也就是$cost_{01} > cost_{10}$，在上例中，$p>0.7$；反之，$p<0.7$。

​ 我們再看下縱軸的定義：
$cost_{norm} = \frac{FNR*p*cost{01} + FPR*(1-p)*cost{10}}{p*cost_{01}+(1-p)cost_{10}} ②$
​ 將②式進行一下變形：
$cost_{norm} = \frac{FNR*p*cost{01}}{p*cost_{01}+(1-p)cost_{10}} + \frac{FPR*(1-p)*cost{10}}{p*cost_{01}+(1-p)cost_{10}}$

$cost_{norm} = FNR*P(+)cost + \frac{FPR*(1-p)*cost{10}}{p*cost_{01}+(1-p)cost_{10}} ③$

​ 再看公式：
$1-P(+)cost =\frac{(1-p)cost_{10}}{p*cost_{01}+(1-p)cost_{10}}$
​ 所以公式③可以變化爲：
$cost_{norm} = FNR*P(+)cost + FPR*(1-P(+)cost) ④$
​ 其中，FNR表示假陰率，也就是正例被錯判爲反例的樣本情況。FPR是假陽率，也就是反例被錯判爲正例的樣本情況。

​ 此時，我們可以把書中的這樣圖貼出來了：

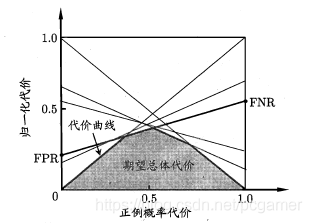
有了上面的公式，我們來看一下這個圖是怎麼畫出來的：

• 首先考察下$(0,FPR)$，$(1,FNR)$這條線段。要搞明白這個線段是怎麼出來的，我們將公式④再做一個小變換：
  $cost_{norm} = (FNR-FPR)P(+)cost + FPR ⑤$
  上面說過了，$P(+)cost$爲橫軸，我們把它看成自變數$x$，$FNR-FPR$看成參數$a$，那麼公式⑤就成了
  $cost_{norm} = ax + FPR$
  這個公式在座標系中就是表示了一條直線，那麼：
  $x = 0, cost_{norm} = FPR$

  $x = 1, cost_{norm} = FNR$

  這就是$(0,FPR)$, $(1,FNR)$線段。

• 上面提到了，$P(+)cost$可以簡單等於樣本正例概率$p$，在含代價資訊的語意下，就是正例的重要程度。我們再來看一下這個$cost_{norm}$是個什麼含義。看一下公式4：其中第一項$FNR*P(+)cost$，FNR表示正例誤判成反例的概率，所以$FNR*P(+)cost$就表示正例誤判成反例的影響程度；而$FPR*(1-P(+)cost)$就表示反例誤判成正例的影響程度。

  所以，縱軸的數位就表示兩者的影響程度相加，線段上的一個點的含義就是在某個樣本正例的比例下， 學習期的誤判影響程度。而整個線段的含義就是，隨着樣本正例的比例增加，影響程度的走向。

• 前面講ROC的時候，我們可以看出，如何對預測值進行閾值劃分，會影響到FPR，FNR，TPR，TNR這四個值，在ROC中，對應的就是圖中的一個一個的點。而在代價曲線中，就是不同的線段，參考第一條，FPR，FNR變了，起點和都會發生變化。

• 在上面一點中提到，在劃分正例/反例的閾值變化時，代價曲線圖中會增加一條。那麼，我們看一下，當正例概率一定的情況下，閾值劃分造成的若幹條線段的區別：
  

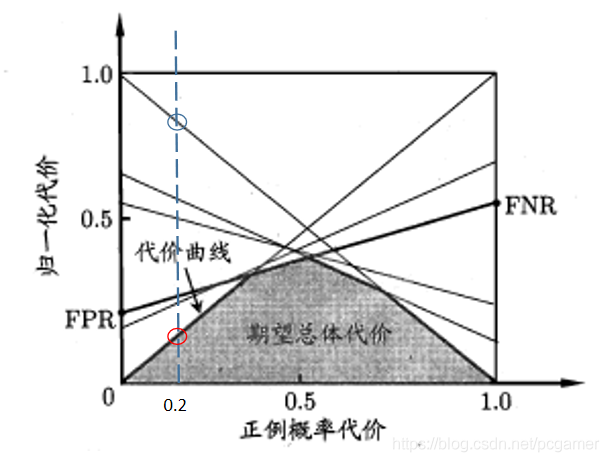
  也就是說，在樣本正例比例 $p=0.2$時(這裏先假定$P(+)cost\approx p$)，紅圈圈出的交叉點代表的那條直線(劃分閾值$\alpha$)的代價最小，藍圈代表的那條直線(劃分閾值$\beta$)代價最大。而我們的目標是要找出代價最低的，那麼此時，我們選擇紅圈所代表的閾值：$\alpha$

  再看一下當$p=0.8$時的情況：
  

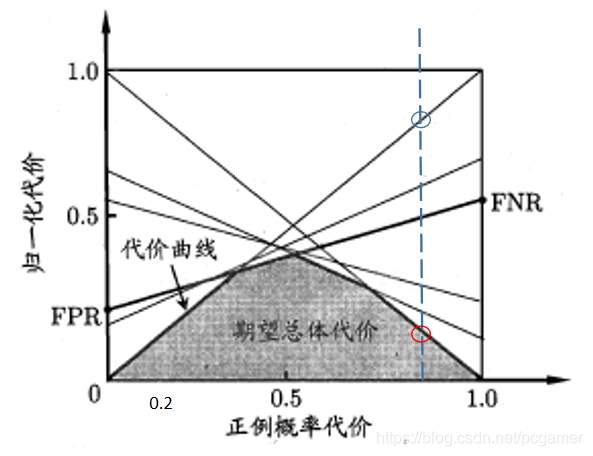
  ​ 可以看出，紅圈代表的曲線是上面提到閾值$\beta$。所以，陰影部分代表的含義，我的理解是當正例比例變化時，在各個閾值中取最小的線段所圍成的區域。

• 我們再看一下$P(+)cost\neq p$的情況，假設正例判盼成反例的的代價$cost_{01} > cost_{10}$，那麼$(0, FPR)$, $(0,FNR)$的曲線會更加向左陡峭一點(如下圖中的虛線，表示全部反例判成正例的代價會小，看$(0,FPR)$這個點，也就是說此時沒有正例樣本，此時反例判成正例的成本是低於原來的那條曲線的)：

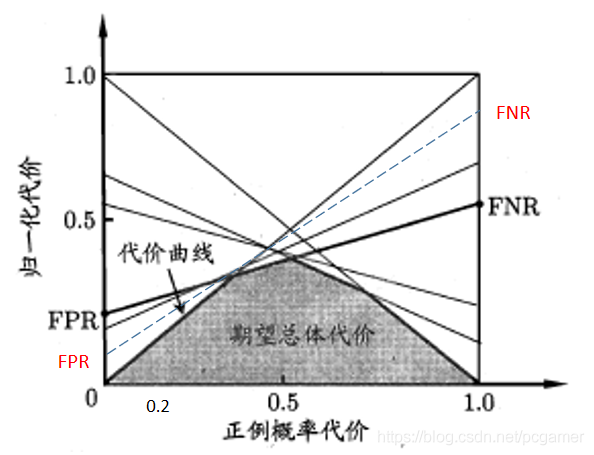
​ 如果是$cost_{01} < cost_{10}$：