老衛帶你學---python使用scipy求解線性規劃問題

老衛帶你學—python使用scipy求解線性規劃問題

線性規劃求解
線性規劃求解主要弄清楚兩個部分，目標函數（max，min）和約束條件（s.t.），我們求解時一般要化爲MATLAB標準形式

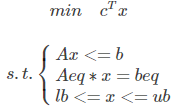
MATLAB求解程式碼爲：

[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
LB,UB分別爲x的上界和下界

在此用Python求解，需要scipy和numpy庫的支援：

from scipy import optimize
import numpy as np

#求解函數
res = optimize.linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
#目標函數最小值
print(res.fun)
#最優解
print(res.x)

例 求解下列線性規劃問題

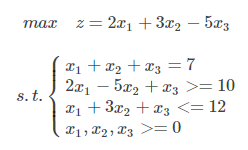
code:

#匯入包
from scipy import optimize
import numpy as np

#確定c,A,b,Aeq,beq
c = np.array([2,3,-5])
A = np.array([[-2,5,-1],[1,3,1]])     ###這裏是二維陣列
b = np.array([-10,12)]
Aeq = np.array([[1,1,1]])     ###這裏是二維陣列
beq = np.array([7])

#求解
res = optimize.linprog(-c,A,b,Aeq,beq)
print(res)

reslult:
     fun: -14.571428571428571
 message: 'Optimization terminated successfully.'
     nit: 2
   slack: array([3.85714286, 0.        ])
  status: 0
 success: True
       x: array([6.42857143, 0.57142857, 0.        ])

可以看到求解的結果，我們關注第一個和最後一個，fun就是目標函數最小值，x就是最優解。
注：在求解時帶入-c並且把第二個式子的係數加了負號，是因爲需要化爲MATLAB標準形式，最終求出來的值爲最小值即-14.57，去掉負號就是我們要的最大值。

由於求解的是目標函數是最小值的問題，但如果我們的目標函數是求最大值，可以通過對目標函數中每一項中乘以-1，將求最大值問題轉化爲求最小值問題；