技術文章 » 機器學習之LDA線性判別分析

機器學習之LDA線性判別分析

2020-08-10 16:29:30

思想總結

線性判別分析( Linear Discriminant Analysis , LDA )是一種經典的降維方法。和主成分分析 PCA 不
考慮樣本類別輸出的無監督降維技術不同, LDA 是一種監督學習的降維技術,數據集的每個樣本有類別輸出。

LDA 分類思想簡單總結如下:

  • 多維空間中,數據處理分類問題較爲複雜, LDA 演算法將多維空間中的數據投影到一條直線上,將 d
    維數據轉化成 1 維數據進行處理。
  • 對於訓練數據,設法將多維數據投影到一條直線上,同類數據的投影點儘可能接近,異類數據點盡
    可能遠離。
  • 對數據進行分類時,將其投影到同樣的這條直線上,再根據投影點的位置來確定樣本的類別。
    如果用一句話概括 LDA 思想,即 「 投影後類內方差最小,類間方差最大 」 。

圖解 LDA 核心思想

假設有紅、藍兩類數據,這些數據特徵均爲二維,如下圖所示。我們的目標是將這些數據投影到一維,讓每一類相近的數據的投影點儘可能接近,不同類別數據儘可能遠,即圖中紅色和藍色數據中心之間的距離儘可能大。
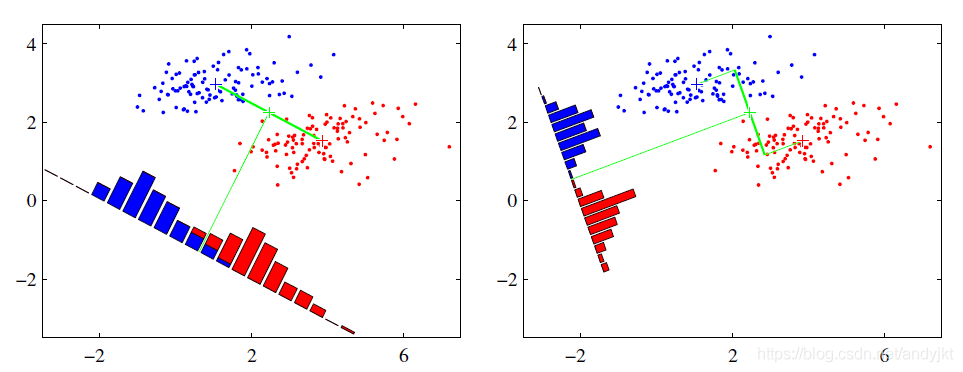
在这里插入图片描述
左圖和右圖是兩種不同的投影方式。

  • 左圖思路:讓不同類別的平均點距離最遠的投影方式。
  • 右圖思路:讓同類別的數據捱得最近的投影方式。

從上圖直觀看出,右圖紅色數據和藍色數據在各自的區域來說相對集中,根據數據分佈直方圖也可看出,所以右圖的投影效果好於左圖,左圖中間直方圖部分有明顯交集。
以上例子是基於數據是二維的,分類後的投影是一條直線。如果原始數據是多維的,則投影後的分類面是一低維的超平面。

二類LDA演算法原理

輸入:數據集 D=(x1,y1),(x2,y2),...,(xm,ym)D={(\boldsymbol x_1,\boldsymbol y_1),(\boldsymbol x_2,\boldsymbol y_2),...,(\boldsymbol x_m, \boldsymbol y_m)},其中樣本 xi\boldsymbol x_i 是 n 維向量, yiϵ0,1\boldsymbol y_i \epsilon{0, 1} ,降維後的目標維度 dd 。定義
Nj(j=0,1)N_j(j=0,1) 爲第 jj 類樣本個數;
Xj(j=0,1)X_j(j=0,1) 爲第 jj 類樣本的集合;
uj(j=0,1)u_j(j=0,1) 爲第 jj 類樣本的均值向量;
∑j(j=0,1)\sum_j(j=0,1) 爲第 jj 類樣本的協方差矩陣。
其中
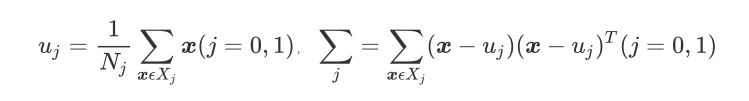
在这里插入图片描述
假設投影直線是向量 w\boldsymbol w ,對任意樣本 xi\boldsymbol x_i ,它在直線 ww 上的投影爲wTxi\boldsymbol w^Tx_i ,兩個類別的中心點 u0u_0, u1u_1 在直線 ww 的投影分別爲wTu0\boldsymbol w^Tu_0 、 wTu1\boldsymbol w^Tu_1 。

LDA 的目標是讓兩類別的數據中心間的距離 ∣wTu0−wTu1∣22| \boldsymbol w^Tu_0 - \boldsymbol w^Tu_1|^2_2 儘量大,與此同時,希望同類樣本投影點的協方差 wT∑0w\boldsymbol w^T \sum_0\boldsymbol w 、wT∑1w\boldsymbol w^T \sum_1 \boldsymbol w 儘量小,最小化 wT∑0w+wT∑1w\boldsymbol w^T \sum_0\boldsymbol w + \boldsymbol w^T \sum_1 \boldsymbol w 。

定義類內散度矩陣
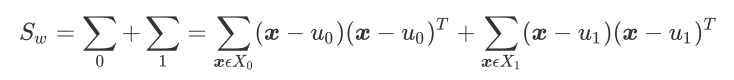
在这里插入图片描述
類間散度矩陣 Sb=(u0−u1)(u0−u1)TS_b = (u_0 - u_1)(u_0 - u_1)^T

據上分析,優化目標爲
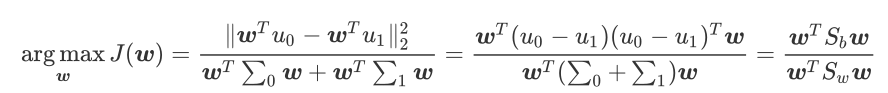
在这里插入图片描述
根據廣義瑞利商的性質,矩陣 S−1wSbS^{-1}{w} S_b 的最大特徵值爲 J(w)J(\boldsymbol w) 的最大值,矩陣S−1wSbS^{-1}{w} S_b 的最大特徵值對應的特徵向量即爲 w\boldsymbol w 。

LDA演算法流程總結

演算法降維流程如下:
輸入:數據集 D=(x1,y1),(x2,y2),...,(xm,ym)D = { (x_1,y_1),(x_2,y_2), ... ,(x_m,y_m) } ,其中樣本 xix_i 是 n 維向量, yiϵC1,C2,...,Cky_i \epsilon {C_1, C_2, ..., C_k} ,降維後的目標維度 dd 。
輸出:降維後的數據集 D‾\overline{D} 。
步驟:

  • 計算類內散度矩陣 SwS_w 。
  • 計算類間散度矩陣 SbS_b 。
  • 計算矩陣 Sw−1SbS^{-1}_wS_b 。
  • 計算矩陣 Sw−1SbS^{-1}_wS_b 的最大的 d 個特徵值。
  • 計算 d 個特徵值對應的 d 個特徵向量,記投影矩陣爲 W 。
  • 轉化樣本集的每個樣本,得到新樣本 Pi=WTxiP_i = W^Tx_i 。
  • 輸出新樣本集 D‾=(p1,y1),(p2,y2),...,(pm,ym)\overline{D} = { (p_1,y_1),(p_2,y_2),...,(p_m,y_m) }

LDA優缺點

優點

  • 可以使用類別的先驗知識
  • 以標籤,類別衡量差異性的有監督降維方式,相對於PCA的模糊性,其目的更明確,更能反映樣本間的差異

缺點

  • LDA不適合對非高斯分佈樣本進行降維
  • LDA降維最多降到分類數k-1維
  • LDA在樣本分類資訊依賴方差而不是均值時,降維效果不好
  • LDA可能過度擬合數據

LDA和PCA的區別

相同點

  • 兩者俊可以對數據進行降維
  • 兩者在降維時均使用了矩陣特徵分解的思想
  • 兩者都假設數據符合高斯分佈

不同點

LDA PCA
有監督 無監督
降維最多降到k-1維 降維多少沒有限制
可以用於降維,還可以用於分類 只用於降維
選擇分類效能最好的投影方向 選擇樣本點投影具有最大方差的方向
更明確,更能反應樣本間的差異 目的較爲模糊