Fully Convolutional Networks for Semantic Segmentation

Jonathan Long∗ Evan Shelhamer∗ Trevor Darrell UC Berkeley {jonlong,shelhamer,trevor}@cs.berkeley.edu Jonathan Long∗ Evan Shelhamer∗ Trevor Darrell UC Berkeley {jonlong,shelhamer,trevor}@cs.berkeley.edu

Abstract

Convolutional networks are powerful visual models that yield hierarchies of features. We show that convolutional networks by themselves, trained end-to-end, pixelsto-pixels, exceed the state-of-the-art in semantic segmentation. Our key insight is to build 「fully convolutional」 networks that take input of arbitrary size and produce correspondingly-sized output with efficient inference and learning. We define and detail the space of fully convolutional networks, explain their application to spatially dense prediction tasks, and draw connections to prior models. We adapt contemporary classification networks (AlexNet [20], the VGG net [31], and GoogLeNet [32]) into fully convolutional networks and transfer their learned representations by fine-tuning [3] to the segmentation task. We then define a skip architecture that combines semantic information from a deep, coarse layer with appearance information from a shallow, fine layer to produce accurate and detailed segmentations. Our fully convolutional net-work achieves stateof-the-art segmentation of PASCAL VOC (20% relative improvement to 62.2% mean IU on 2012), NYUDv2, and SIFT Flow, while inference takes less than one fifth of a second for a typical image.

摘要

  折積網路是可以產生特徵層次的強大視覺化模型。我們表明，折積網路本身，經過端到端，畫素到畫素的訓練，在語意分割方面超過了最先進的水平。我們的主要見解是建立「 全折積」網路，該網路可接受任意大小的輸入，並通過有效的推理和學習產生相應大小的輸出。我們定義並詳細說明了完全折積網路的空間，解釋了它們在空間密集預測任務中的應用，並闡述了與先前模型的聯繫。我們將當代分類網路(AlexNet [20]、VGG網路[31]和GoogLeNet [32])改造成完全折積網路，並通過微調[3]將它們的學習表示轉移到分割任務中。然後，我們定義了一個跳躍結構，它將來自深度粗糙層的語意資訊與來自淺層精細層的外觀資訊相結合，以生成準確和詳細的分割。我們的全折積網路實現了對PASCAL VOC(相對於2012年62.2%的平均IU改進率爲20%)、NYUDv2和SIFT Flow的最先進的分割，而對於典型的影象，推斷時間不到五分之一秒。

1.Introduction

Convolutional networks are driving advances in recognition. Convnets are not only improving for whole-image classification [20, 31, 32], but also making progress on local tasks with structured output. These include advances in bounding box object detection [29, 10, 17], part and keypoint prediction [39, 24], and local correspondence [24, 8].

The natural next step in the progression from coarse to fine inference is to make a prediction at every pixel. Prior approaches have used convnets for semantic segmentation [27, 2, 7, 28, 15, 13, 9], in which each pixel is labeled with the class of its enclosing object or region, but with shortcomings that this work addresses.

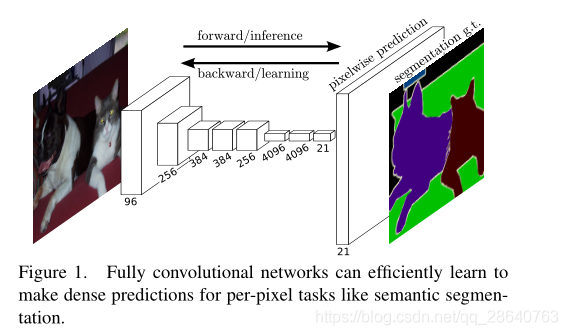
We show that a fully convolutional network (FCN) trained end-to-end, pixels-to-pixels on semantic segmentation exceeds the state-of-the-art without further machinery. To our knowledge, this is the first work to train FCNs end-to-end (1) for pixelwise prediction and (2) from supervised pre-training. Fully convolutional versions of existing networks predict dense outputs from arbitrary-sized inputs. Both learning and inference are performed whole-image-ata-time by dense feedforward computation and backpropagation. In-network upsampling layers enable pixelwise prediction and learning in nets with subsampled pooling.

This method is efficient, both asymptotically and absolutely, and precludes the need for the compli-cations in other works. Patchwise training is common [27, 2, 7, 28, 9], but lacks the efficiency of fully convolutional training. Our approach does not make use of pre- and post-processing complications, including superpixels [7, 15], proposals [15, 13], or post-hoc refinement by random fields or local class-ifiers [7, 15]. Our model transfers recent success in classification [20, 31, 32] to dense prediction by reinterpreting classification nets as fully convolutional and fine-tuning from their learned representa-tions. In contrast, previous works haveappliedsmallconvnetswithoutsupervisedpre-training [7, 28, 27].

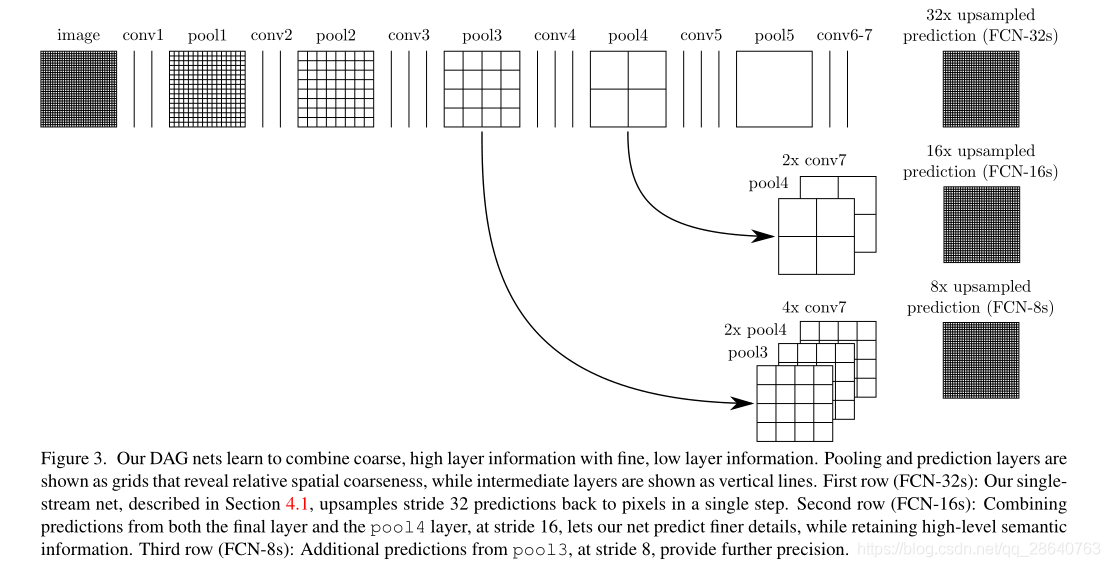
Semantic segmentation faces an inherent tension between semantics and location: global information resolves what while local information resolves where. Deep feature hierarchies encode location and semantics in a nonlinear local-to-global pyramid. We define a skip architecture to take advantage of this feature spectrum that combines deep, coarse, semantic information and shallow, fine, appearance information in Section 4.2 (see Figure 3).

In the next section, we review related work on deep classification nets, FCNs, and recent approaches to semantic segmentation using convnets. The following sections explain FCN design and dense prediction tradeoffs, introduce our architecture with in-network upsampling and multilayer combinations, and describe our experimental framework. Finally, we demonstrate state-of-the-art results on PASCAL VOC 2011-2, NYUDv2, and SIFT Flow.

1.引言

  折積網路正在推動識別技術的進步。折積網路不僅在改善了整體影象分類[20，31，32]，而且還在具有結構化輸出的區域性任務上也取得了進展。這些進展包括邊界框目標檢測[29，10，17]，部分和關鍵點預測[39，24]，以及區域性對應[24，8]。

  從粗略推斷到精細推理，很自然下一步是對每個畫素進行預測。先前的方法已經使用了折積網路用於語意分割[27，2，7，28，15，13，9]，其中每個畫素都用其包圍的物件或區域的類別來標記，但是存在該工作要解決的缺點。

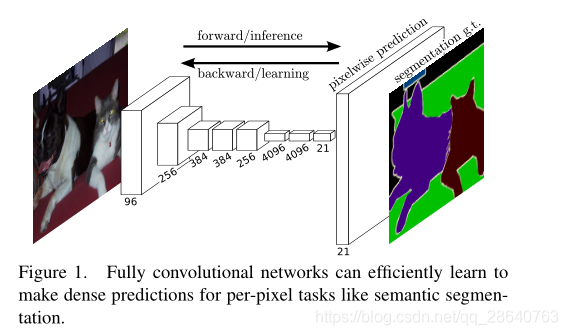
  我們表明瞭在語意分割上，經過端到端，畫素到畫素訓練的完全折積網路（FCN）超過了最新技術，而無需其他機制 機製。據我們所知，這是第一個從（2）有監督的預訓練，端到端訓練地FCN（1）用於畫素預測。現有網路的完全折積版本可以預測來自任意大小輸入的密集輸出。學習和推理都是通過密集的前饋計算和反向傳播在整個影象上進行的。網路內上採樣層通過子採樣池化來實現網路中的畫素預測和學習。

  這種方法在漸近性和絕對性兩方面都是有效的，並且排除了對其他工作中的複雜性的需要。逐塊訓練是很常見的[27,2,8,28,11]，但缺乏完全折積訓練的效率。我們的方法沒有利用前後處理的複雜性，包括超畫素[8,16]，建議[16,14]，或通過隨機欄位或區域性分類器進行事後細化[8,16]。我們的模型通過將分類網路重新解釋爲完全折積並從其學習的表示中進行微調，將最近在分類任務[19,31,32]中取得的成功轉移到密集預測任務。相比之下，以前的工作是在沒有經過有監督的預訓練的情況下應用了小型折積網路[7，28，27]。

  語意分割面臨着語意和位置之間的固有矛盾：全域性資訊解決了什麼，而區域性資訊解決了什麼。 深度特徵層次結構以非線性的區域性到全域性金字塔形式對位置和語意進行編碼。 在4.2節中，我們定義了一個跳躍結構來充分利用這種結合了深層，粗略，語意資訊和淺層，精細，外觀資訊的特徵譜（請參見圖3）。

  在下一節中，我們將回顧有關深度分類網，FCN和使用折積網路進行語意分割的最新方法的相關工作。 以下各節介紹了FCN設計和密集的預測權衡，介紹了我們的具有網路內上採樣和多層組合的架構，並描述了我們的實驗框架。 最後，我們演示了PASCAL VOC 2011-2，NYUDv2和SIFT Flow的最新結果。

2.Related work

Our approach draws on recent successes of deep nets for image classification [20, 31, 32] and transfer learning [3, 38]. Transfer was first demonstrated on various visual recognition tasks [3, 38], then on detection, and on both instance and semantic segmentation in hybrid proposalclassifier models [10, 15, 13]. We now re-architect and finetune classification nets to direct, dense prediction of semantic seg-mentation. We chart the space of FCNs and situate prior models, both historical and recent, in this framework.

Fully convolutional networks To our knowledge, the idea of extending a convnet to arbitrary-sized inputs first appeared in Matan et al. [26], which extended the classic LeNet [21] to recognize strings of digits. Because their net was limited to one-dimensional input strings, Matan et al. used Viterbi decoding to obtain their outputs. Wolf and Platt [37] expand convnet outputs to 2-dimensional maps of detection scores for the four corners of postal address blocks. Both of these historical works do inference and learning fully convolutionally for detection. Ning et al. [27] define a convnet for coarse multiclass segmentation of C. elegans tissues with fully convolutional inference.

Fully convolutional computation has also been exploited in the present era of many-layered nets. Sliding window detection by Sermanet et al. [29], semantic segmentation by Pinheiro and Collobert [28], and image restoration by Eigen et al. [4] do fully convolutional inference. Fully convolutional training is rare, but used effectively by Tompson et al. [35] to learn an end-to-end part detector and spatial model for pose estimation, although they do not exposit on or analyze this method.

Alternatively, He et al. [17] discard the nonconvolutional portion of classification nets to make a feature extractor. They combine proposals and spatial pyramid pooling to yield a localized, fixed-length feature for classification. While fast and effective, this hybrid model cannot be learned end-to-end.

Dense prediction with convnets Several recent works have applied convnets to dense prediction problems, including semantic segmentation by Ning et al. [27], Farabet et al.[7], and Pinheiro and Collobert [28]; boundary prediction for electron microscopy by Ciresan et al. [2] and for natural images by a hybrid convnet/nearest neighbor model by Ganin and Lempitsky [9]; and image restoration and depth estimation by Eigen et al. [4, 5]. Common elements of these approaches include
• small models restricting capacity and receptive fields;
• patchwise training [27, 2, 7, 28, 9];
• post-processing by superpixel projection, random field regularization, filtering, or local classification [7, 2, 9];
• input shifting and output interlacing for dense output [29, 28, 9];
• multi-scale pyramid processing [7, 28, 9];
• saturating tanh nonlinearities [7, 4, 28]; and
• ensembles [2, 9],
whereas our method does without this machinery. However, we do study patchwise training 3.4 and 「shift-and-stitch」 dense output 3.2 from the perspective of FCNs. We also discuss in-network upsamp-ling 3.3, of which the fully connected prediction by Eigen et al. [5] is a special case.

Unlike these existing methods, we adapt and extend deep classification architectures, using image classification as supervised pre-training, and fine-tune fully convolutionally to learn simply and eff-iciently from whole image inputs and whole image ground thruths.

Hariharan et al. [15] and Gupta et al. [13] likewise adapt deep classification nets to semantic segmen-tation, but do so in hybrid proposal-classifier models. These approaches fine-tune an R-CNN system [10] by sampling bounding boxes and/or region proposals for detection, semantic segmentation, and instance segmentation. Neither method is learned end-to-end. They achieve state-of-the-art segmen-tation results on PASCAL VOC and NYUDv2 respectively, so we directly compare our standalone, end-to-end FCN to their semantic segmentation results in Section 5.

We fuse features across layers to defineanonlinearlocalto-global representation that we tune end-to-end. In contemporary work Hariharan et al. [16] also use multiple layers in their hybrid model for se-mantic segmentation.

2.相關工作

  我們的方法借鑑了最近成功的用於影象分類[20, 31, 32]和遷移學習[3,38]的深度網路。遷移首先在各種視覺識別任務[3,38]，然後是檢測，以及混合提議分類器模型中的範例和語意分割任務[10,15,13]上進行了演示。我們現在重新構建和微調分類網路，來直接，密集地預測語意分割。我們繪製了FCN的空間，並在此框架中放置了歷史和近期的先前模型。

  全折積網路 據我們所知，Matan等人首先提出了將一個折積網路擴充套件到任意大小的輸入的想法。 [26]，它擴充套件了classicLeNet [21]來識別數位串。因爲他們的網路被限製爲一維輸入字串，所以Matan等人使用Viterbi解碼來獲得它們的輸出。Wolf和Platt [37]將折積網路輸出擴充套件爲郵政地址塊四個角的檢測分數的二維圖。這兩個歷史工作都是通過完全折積進行推理和學習，以便進行檢測。 寧等人 [27]定義了一個折積網路，通過完全折積推理對秀麗隱桿線蟲組織進行粗多類分割。

在當前的多層網路時代，全折積計算也已經得到了利用。Sermanet等人的滑動視窗檢測 [29]，Pinheiro和Collobert [28]的語意分割，以及Eigen等人的影象恢復 [4]都做了全折積推理。全折積訓練很少見，但Tompson等人有效地使用了它 [35]來學習一個端到端的部分探測器和用於姿勢估計的空間模型，儘管他們沒有對這個方法進行解釋或分析。

或者，He等人 [17]丟棄分類網路的非折積部分來製作特徵提取器。它們結合了建議和空間金字塔池，以產生用於一個區域性化，固定長度特徵的分類。雖然快速有效，但這種混合模型無法進行端到端地學習。

  用折積網路進行密集預測 最近的一些研究已經將折積網路應用於密集預測問題，包括Ning等[27]，Farabet等[7]，Pinheiro和Collobert 等[28] ；Ciresan等人的電子顯微鏡邊界預測[2]，Ganin和Lempitsky的混合折積網路/最近鄰模型的自然影象邊界預測[9]；Eigen等人的影象恢復和深度估計 [4,5]。這些方法的共同要素包括：
• 限制容量和感受野的小模型;
• 逐塊訓練[27, 2, 7, 28, 9];
• 有超畫素投影，隨機場正則化，濾波或區域性分類[7,2,9]的後處理過程;
• 密集輸出的輸入移位和輸出交錯[29,28,9];
• 多尺度金字塔處理[7,28,9];
• 飽和tanh非線性[7,4,28];
• 整合[2,9]
而我們的方法沒有這種機制 機製。然而，我們從FCN的角度研究了逐塊訓練3.4節和「移位 - 連線」密集輸出3.2節。我們還討論了網路內上採樣3.3節，其中Eigen等人的全連線預測 [6]是一個特例。

與這些現有方法不同，我們採用並擴充套件了深度分類架構，使用影象分類作爲有監督的預訓練，並通過全折積微調，以簡單有效的從整個影象輸入和整個影象的Ground Truths中學習。

Hariharan等人 [15]和Gupta等人 [13]同樣使深度分類網適應語意分割，但只在混合建議 - 分類器模型中這樣做。這些方法通過對邊界框和/或候選域採樣來微調R-CNN系統[10]，以進行檢測，語意分割和範例分割。這兩種方法都不是端到端學習的。他們分別在PASCAL VOC和NYUDv2實現了最先進的分割成果，因此我們直接在第5節中將我們的獨立端到端FCN與他們的語意分割結果進行比較。

我們融合各層的特徵去定義一個我們端到端調整的非線性區域性到全域性的表示。在當代工作中，Hariharan等人[16]也在其混合模型中使用了多層來進行語意分割。

3.Fully convolutional networks

Each layer of data in a convnet is a three-dimensional array of size h × w × d, where h and w are spatial dimensions, and d is the feature or channel dimension. The first layer is the image, with pixel size h × w, and d color channels. Locations in higher layers correspond to the locations in the image they are path-connected to, which are called their receptive fields.

Convnets are built on translation invariance. Their basic components (convolution, pooling, and acti-vation functions) operate on local input regions, and depend only on relative spatial coordinates. Writ-ing $X_{ij}$for the data vector at location (i, j) in a particular layer, and $y_{ij}$ for the following layer, these functions compute outputs $y_{ij}$ by
$y_{ij} = f_{ks}(\{x_{si+\delta i,sj+\delta j}\}_{0\le \delta i,\delta j \le k})$
where k is called the kernel size, s is the stride or subsampling factor, and $f_{ks}$ determines the layer type: a matrix multiplication for convolution or average pooling, a spatial max for max pooling, or an elementwise nonlinearity for an activation function, and so on for other types of layers.

This functional form is maintained under composition,with kernel size and stride obeying the trans-formation rule
$f_{ks}\circ g_{k's'} = (f\circ g)_{k'+(k-1)s',ss'}.$
While a general deep net computes a general nonlinear function, a net with only layers of this form computes a nonlinear filter, which we call a deep filter or fully convolutional network. An FCN naturally operates on an input of any size, and produces an output of corresponding (possibly resampled) spatial dimensions.

A real-valued loss function composed with an FCN defines a task. If the loss function is a sum over the spatial dimensions of the final layer, $l(x;θ) =\sum_{ ij}l'(x_{ij};θ)$, its gradient will be a sum over the gra-dients of each of its spatial components. Thus stochastic gradient descent on $l$ computed on whole images will be the same as stochastic gradient descent on $l'$, taking all of the final layer receptive fields as a minibatch.

When these receptive fields overlap significantly, both feedforward computation and backpropagation are much more efficient when computed layer-by-layer over an entire image instead of independently patch-by-patch.

We next explain how to convert classification nets into fully convolutional nets that produce coarse output maps. For pixelwise prediction, we need to connect these coarse outputs back to the pixels. Section 3.2 describes a trick, fast scanning [11], introduced for this purpose. We gain insight into this trick by reinterpreting it as an equivalent network modification. As an efficient, effective alternative, we introduce deconvolution layers for upsampling in Section 3.3. In Section 3.4 we consider training by patchwise sampling, and give evidence in Section 4.3 that our whole image training is faster and equally effective.

3.全折積網路

  折積網路中的每一層數據都是大小爲h×w×d的三維陣列，其中h和w是空間維度，d是特徵或通道維度。第一層是有着畫素大小爲h×w，以及d個顏色通道的影象，較高層中的位置對應於它們路徑連線的影象中的位置，這些位置稱爲其感受野。

  卷及網路建立在平移不變性的基礎之上。它們的基本組成部分（折積，池化和啓用函數）作用於區域性輸入區域，並且僅依賴於相對空間座標。用$X_{ij}$表示特定層位置（x,j）處的數據向量，$y_{ij}$表示下一層的數據向量，可以通過下式來計算$y_{ij}$:
$y_{ij} = f_{ks}(\{x_{si+\delta i,sj+\delta j}\}_{0\le \delta i,\delta j \le k})$
其中k稱爲內核大小，s爲步長或者子採樣因子，$f_{ks}$決定層的型別：用於折積或平均池化的矩陣乘法，用於最大池化的空間最大值，或用於啓用函數的非線性元素，用於其他型別的層等等。

這種函數形式在組合下維護，內核大小和步長遵守轉換規則：
$f_{ks}\circ g_{k's'} = (f\circ g)_{k'+(k-1)s',ss'}.$
當一般的深度網路計算一般的非線性函數，只有這種形式的層的網路計算非線性濾波器，我們稱之爲深度濾波器或完全折積網路。FCN自然地對任何大小的輸入進行操作，併產生相應（可能重採樣）空間維度的輸出。

  由FCN組成的實值損失函數定義了任務。如果損失函數是最終層的空間維度的總和， $l(x;θ) =\sum_{ ij}l'(x_{ij};θ)$,它的梯度將是每個空間分量的梯度之和。因此，對整個影象計算的 $l$ 的隨機梯度下降將與將所有最終層感受野視爲小批次的 $l'$ 上的隨機梯度下降相同。

  當這些感受野顯着重疊時，前饋計算和反向傳播在整個影象上逐層計算而不是單獨逐塊計算時效率更高。

  接下來，我們將解釋如何將分類網路轉換爲產生粗輸出圖的完全折積網路。對於逐畫素預測，我們需要將這些粗略輸出連線回畫素。第3.2節爲此目的引入了一個技巧，即快速掃描[11]。我們通過將其重新解釋爲等效的網路修改來深入瞭解這一技巧。作爲一種有效的替代方案，我們在第3.3節中介紹了用於上採樣的反捲積層。在第3.4節中，我們考慮了通過逐點抽樣進行的訓練，並在第4.3節中給出了證據，證明我們的整體影象訓練更快且同樣有效。

3.1. Adapting classifiers for dense prediction

Typical recognition nets, including LeNet [21], AlexNet [20], and its deeper successors [31, 32], ostensibly take fixed-sized inputs and produce non-spatial outputs. The fully connected layers of these nets have fixed dimensions and throw away spatial coordinates. However, these fully connected layers can also be viewed as convolutions with kernels that cover their entire input regions. Doing so casts them into fully convolutional networks that take input of any size and output classification maps. This transformation is illustrated in Figure 2.

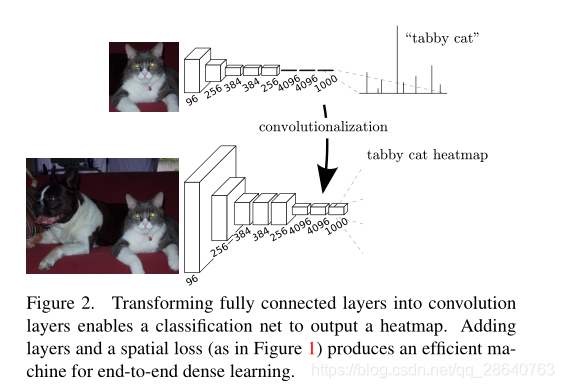
Furthermore, while the resulting maps are equivalent to the evaluation of the original net on particular input patches, the computation is highly amortized over the overlapping regions of those patches. For example, while AlexNet takes 1.2 ms (on a typical GPU) to infer the classification scores of a 227×227 image, the fully convolutional net takes 22ms to produce a 10×10 grid of outputs from a 500×500 image, which is more than 5 times faster than the na¨ ıve approach1.

The spatial output maps of these convolutionalized models make them a natural choice for dense problems like semantic segmentation. With ground truth available at every output cell, both the forward and backward passes are straightforward, and both take advantage of the inherent computational efficiency (and aggressive optimization) of convolution. The corresponding backward times for the AlexNet example are 2.4 ms for a single image and 37 ms for a fully convolutional 10 × 10 output map, resulting in a speedup similar to that of the forward pass.

While our reinterpretation of classification nets as fully convolutional yields output maps for inputs of any size, the output dimensions are typically reduced by subsampling. The classification nets sub-sample to keep filters small and computational requirements reasonable. This coarsens the output of a fully convolutional version of these nets, reducing it from the size of the input by a factor equal to the pixel stride of the receptive fields of the output units.

3.1. 調整分類器以進行密集預測

  典型的識別網路，包括LeNet [21]、AlexNet [20]及其更深層的後繼網路[31、32]，表面上接受固定大小的輸入併產生非空間輸出。這些網路的全連線層具有固定的尺寸並且丟棄了空間座標。然而，這些完全連線的層也可以被視爲具有覆蓋其整個輸入區域的內核的折積。這樣做將它們轉換成完全折積的網路，該網路可以接受任何大小的輸入並輸出分類圖。這個轉換如圖2所示。（相比之下，非折積網，例如Le等人[20]的網路，缺乏這種能力。）

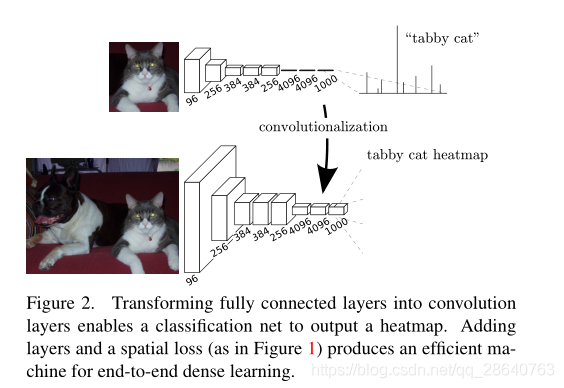
  此外，儘管生成的圖等效於在特定輸入塊上對原始網路的評估，但在這些塊的重疊區域上進行了高額攤銷。例如，雖然AlexNet花費1.2毫秒（在典型的GPU上）來產生 227×227 影象的分類分數，但是全折積網路需要22毫秒才能 纔能從500×500影象中生成10×10的輸出網格，比現在的方法快5倍以上。

  這些折積模型的空間輸出圖使它們成爲語意分割等密集問題的自然選擇。由於每個輸出單元都有可用的Ground Truth，前向和後向傳遞都很簡單，並且都利用了折積的固有計算效率（和主動優化）。AlexNet範例的相應後向時間對於單個影象是2.4ms，對於完全折積10×10輸出對映是37ms，導致類似於前向傳遞的加速。

  儘管我們將分類網路重新解釋爲完全折積，可以得到任何大小的輸入的輸出圖，但輸出維度通常通過二次取樣來減少。分類網路子採樣以保持過濾器較小並且計算要求合理。這使這些網路的完全折積版本的輸出變得粗糙，將其從輸入的大小減少到等於輸出單元的感受野的畫素跨度的因子。

3.2. Shift-and-stitch is filter rarefaction

Dense predictions can be obtained from coarse outputs by stitching together output from shifted versions of the input. If the output is downsampled by a factor of $f$, shift the input $x$ pixels to the right and $y$ pixels down, once for every ($x$, $y$) s.t. 0 ≤$x$, $y$ < $f$. Process each of these $f^2$inputs, and interlace the outputs so that the predictions correspond to the pixels at the centers of their receptive fields.

Although performing this transformation na¨ ıvely increases the cost by a factor of $f^2$, there is a well-known trick for efficiently producing identical results [11, 29] known to the wavelet community as the à trous algorithm [25]. Consider a layer (convolution or pooling) with input stride s, and a subsequent convolution layer with filter weights $f_{ij}$(eliding the irrelevant feature dimensions). Setting the lower layer’s input stride to 1 upsamples its output by a factor of $s$. However, convolving the original filter with the upsampled output does not produce the same result as shift-and-stitch, because the original filter only sees a reduced portion of its (now upsampled) input. To reproduce the trick, rarefy the filter by enlarging it as
$f'_{ij} = \begin{cases} f_{i/s,j/s}, & if s\ divides\ both\ i\ and\ j; \\ 0, & otherwise, \end{cases}$
(with $i$ and $j$ zero-based). Reproducing the full net output of the trick involves repeating this filter enlargement layerby-layer until all subsampling is removed. (In practice, this can be done efficiently by processing subsampled versions of the upsampled input.)

Decreasingsubsamplingwithinanetisatradeoff: thefilters see finer information, but have smaller receptive fields and take longer to compute. The shift-and-stitch trick is another kind of tradeoff: the output is denser without decreasing the receptive field sizes of the filters, but the filters are prohibited from accessing information at a finer scale than their original design.

Although we have done preliminary experiments with this trick, we do not use it in our model. We find learning through upsampling, as described in the next section, to be more effective and efficient, especially when combined with the skip layer fusion described later on.

3.2 移位和拼接是過濾器稀疏

  通過輸入的不同版本的輸出拼接在一起，可以從粗糙的輸出中獲得密集預測。如果輸出被$f$因子下採樣，對於每個($x$, $y$) ，輸入向右移$x$個畫素，向下移$y$個畫素（左上填充），s.t. 0 ≤$x$, $y$ < $f$。

  儘管執行這種變換會很自然地使成本增加$f^2$倍，但有一個衆所周知的技巧可以有效地產生相同的結果[11，29]，小波界稱之爲à trous演算法[25]。考慮一個具有輸入步幅$s$的層(折積或池化)，以及隨後的具有濾波器權重$f_{ij}$的折積層(省略不相關的特徵尺寸)。將較低層的輸入步幅設定爲1會將其輸出向上採樣一個係數$s$。但是，將原始濾波器與向上採樣的輸出進行折積不會產生與移位拼接相同的結果，因爲原始濾波器只看到其(現在向上採樣的)輸入的減少部分。要重現該技巧的話，請將過濾器放大爲
$f'_{ij} = \begin{cases} f_{i/s,j/s}, & if s\ divides\ both\ i\ and\ j; \\ 0, & otherwise, \end{cases}$
（其中$i$和$j$從零開始）。再現技巧的完全網路輸出涉及逐層重複放大此濾波器，直到刪除所有子採樣爲止。 （實際上，可以通過處理上採樣輸入的子採樣版本來有效地完成此操作。）

  減少網路內的二次採樣是一個權衡：過濾器看到更精細的資訊，但是感受野更小，計算時間更長。移位和拼接技巧是另一種權衡:在不減小濾波器感受野大小的情況下，輸出更密集，但是濾波器被禁止以比其原始設計更精細的尺度存取資訊。

  雖然我們已經用這個技巧做了初步的實驗，但是我們沒有在我們的模型中使用它。我們發現通過上採樣進行學習（如下一節所述）更加有效和高效，尤其是與後面描述的跳躍層融合相結合時。

3.3.Upsampling is backwards strided convolution

Another way to connect coarse outputs to dense pixels is interpolation. For instance, simple bilinear interpolation computes each output $y_{ij}$from the nearest four inputs by a linear map that depends only on the relative positions of the input and output cells.

In a sense, upsampling with factor $f$ is convolution with a fractional input stride of $1/f$. So long as $f$ is integral, a natural way to upsample is therefore backwards convolution (sometimes called deconvolution) with an output stride of $f$. Such an operation is trivial to implement, since it simply reverses the forward and backward passes of convolution. Thus upsampling is performed in-network for end-to-end learning by backpropagation from the pixelwise loss.

Note that the deconvolution filter in such a layer need not be fixed (e.g., to bilinear upsampling), but can be learned. A stack of deconvolution layers and activation functions can even learn a nonlinear upsampling.

In our experiments, we find that in-network upsampling is fast and effective for learning dense prediction. Our best segmentation architecture uses these layers to learn to upsample for refined prediction in Section 4.2.

3.3. 上採樣是反向跨步的折積

  將粗糙輸出連線到密集畫素的另一種方法是插值。例如，簡單的雙線性插值通過一個只依賴於輸入和輸出單元的相對位置的線性對映，從最近的四個輸入計算每個輸出$y_{ij}$。

  從某種意義上講，使用因子$f$進行上採樣是對輸入步長爲$1/f$的折積。只要$f$是整數的，那麼向上採樣的自然方法就是輸出步長爲$f$的反向折積（有時稱爲反褶積）。這種操作實現起來很簡單，因爲它只是反轉折積的前進和後退。因此，在網路中進行上採樣可以通過畫素損失的反向傳播進行端到端學習。

  注意，這種層中的反捲積濾波器不需要固定(例如，對於雙線性上採樣)，而是可以學習的。反捲積層和啓用函數的疊加甚至可以學習非線性上採樣。

  在我們的實驗中，我們發現網路內上採樣對於學習密集預測是快速有效的。在第4.2節中，我們的最佳分割架構使用這些層來學習如何對精確預測進行上採樣。

3.4.Patchwise training is loss sampling

In stochastic optimization, gradient computation is driven by the training distribution. Both patchwise training and fully convolutional training can be made to produce any distribution, although their relative computational efficiency depends on overlap and minibatch size. Whole image fully convolutional training is identical to patchwise training where each batch consists of all the receptive fields of the units below the loss for an image (or collection of images). While this is more efficient than uniform sampling of patches, it reduces the number of possible batches. However, random selection of patches within an image may be recovered simply. Restricting the loss to a randomly sampled subset of its spatial terms (or, equivalently applying a DropConnect mask [36] between the output and the loss) excludes patches from the gradient computation.

If the kept patches still have significant overlap, fully convolutional computation will still speed up training. If gradients are accumulated over multiple backward passes, batches can include patches from several images.2

Sampling in patchwise training can correct class imbalance [27, 7, 2] and mitigate the spatial correlation of dense patches [28, 15]. In fully convolutional training, class balance can also be achieved by weighting the loss, and loss sampling can be used to address spatial correlation.

We explore training with sampling in Section 4.3, and do not find that it yields faster or better convergence for dense prediction. Whole image training is effective and efficient.

3.4. 逐塊訓練是採樣損失

  在隨機優化中，梯度計算由訓練分佈驅動。逐塊訓練和全折積訓練都可以產生任何分佈，儘管它們的相對計算效率取決於重疊和小批次大小。整個影象完全折積訓練與逐塊訓練相同，其中每一批都包含低於影象(或影象集合)損失的單元的所有感受野。雖然這比批次的均勻採樣更有效，但它減少了可能的批次數量。然而隨機選擇一幅圖片中patches可以簡單地復現。將損失限製爲其空間項的隨機採樣子集(或者，等效地在輸出和損失之間應用DropConnect掩碼[36])，將patches排除在梯度計算之外。

  如果保留的patches仍然有明顯的重疊，全折積計算仍將加速訓練。如果梯度是通過多次向後傳播累積的，批次可以包括來自多個影象的patches$^2$

  在逐塊訓練中採樣可以糾正類不平衡[27，7，2]並減輕密集patches的空間相關性[28，15]。在全折積訓練中，也可以通過加權損失來實現類平衡，並且可以使用損失採樣來解決空間相關性。

  我們在第4.3節中探討了抽樣訓練，但沒有發現它對密集預測產生更快或更好的收斂。整體形象訓練是有效和高效的。

4.Segmentation Architecture

We cast ILSVRC classifiers into FCNs and augment them for dense prediction with in-network upsamp-ling and a pixelwise loss. We train for segmentation by fine-tuning. Next, we add skips between layers to fuse coarse, semantic and local, appearance information. This skip architecture is learned end-to-end to refine the semantics and spatial precision of the output.

For this investigation, we train and validate on the PASCAL VOC 2011 segmentation challenge [6]. We train with a per-pixel multinomial logistic loss and validate with the standard metric of mean pixel inter-section over union, with the mean taken over all classes, including background. The training ignores pixels that are masked out (as ambiguous or difficult) in the ground truth.

4.分割架構

  我們將ILSVRC分類器轉換成FCN網路，並通過網路內上採樣和畫素級損失來增強它們以進行密集預測。我們通過微調進行分割訓練。接下來，我們在層與層之間新增跳躍結構來融合粗糙的、語意的和區域性的外觀資訊。這種跳躍結構是端到端學習的，以優化輸出的語意和空間精度。

  在本次調查中，我們在PASCAL VOC 2011分割挑戰上進行了訓練和驗證[6]。我們使用每個畫素的多項式邏輯損失進行訓練，並通過聯合上的平均畫素交集的標準度量進行驗證，其中包括所有類的平均值，包括背景。訓練忽略了在ground truth中被掩蓋(如模糊或困難)的畫素。

4.1. From classifier to dense FCN

We begin by convolutionalizing proven classification architectures as in Section 3. We consider the AlexNet architecture that won ILSVRC12, as well as the VGG nets and the GoogLeNet which did exceptionally well in ILSVRC14. We pick the VGG 16-layer net, which we found to be equivalent to the 19-layer net on this task. For GoogLeNet, we use only the final loss layer, and improve performance by discarding the final average pooling layer. We decapitate each net by discarding the final classifier layer, and convert all fully connected layers to convolutions. We append a $1\times 1$ convolution with channel dimension 21 to predict scores for each of the PASCAL classes (including background) at each of the coarse output locations, followed by a (backward) convolution layer to bilinearly upsample the coarse outputs to pixelwise outputs as described in Section 3.3. Table 1 compares the preliminary validation results along with the basic characteristics of each net. We report the best results achieved after convergence at a fixed learning rate (at least 175 epochs).

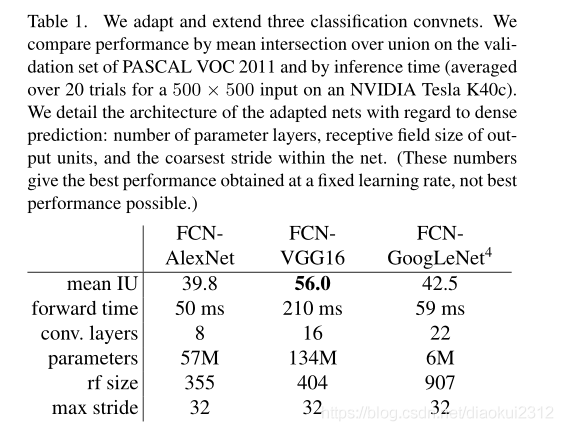
Fine-tuning from classification to segmentation gives reasonable predictions from each net. Even the worst model achieved ~75 percent of the previous best performance.FCN-VGG16 already appears to be state-of-the-art at 56.0 mean IU on val, compared to 52.6 on test [15]. Training on extra data raises FCN-VGG16 to 59.4 mean IU and FCN-AlexNet to 48.0 mean IU on a subset of val7. Despite similar classification accuracy, our implementation of GoogLeNet did not match the VGG16 segmentation result.

4.1 從分類器到密集的FCN

  首先，如第3節所述，對經過驗證的分類體系進行折積。我們考慮贏得ILSVRC12的AlexNet體系結構以及在ILSVRC14中表現出色的VGG網路和GoogLeNet。我們選擇了VGG 16層網路，我們發現它的效果相當於此任務上的19層網路。對於GoogLeNet，我們僅使用最終的損失層，並通過捨棄最終的平均池化層來提高效能。我們通過捨棄最終的分類器層來使擷取每個網路，並將所有全連線層轉換爲折積。我們附加一個具有21通道的$1\times 1$ 折積，以預測每個粗略輸出位置處每個PASCAL類（包括背景）的分數，然後是一個反捲積層，粗略輸出上採樣到畫素密集輸出，如第3.3節所述。表1比較了初步驗證結果以及每個網路的基本特徵。我們報告了以固定的學習速率（至少175 epochs）收斂後獲得的最佳結果。

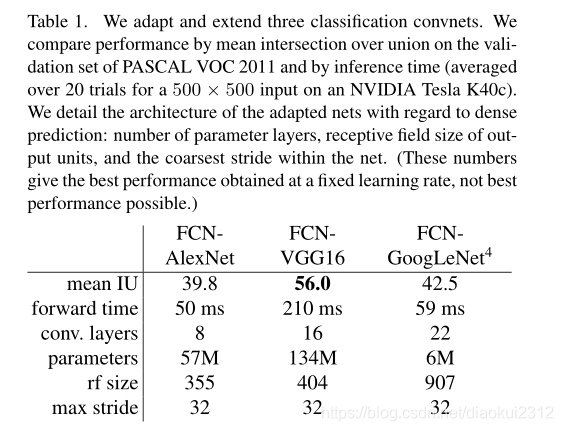
  從分類到分割的微調可爲每個網路提供合理的預測。即使是最糟糕的模型也能達到以前最佳效能的75％。 分割匹配的VGG網路（FCN-VGG16）已經看起來是最先進的，在val上爲56.0平均IU，而在測試中爲52.6 [16]。對額外數據的訓練能將val的子集上將FCN-VGG16的平均IU提高到59.4，FCN-AlexNet的平均IU提高到48.0。儘管分類準確性相似，但我們對GoogLeNet的實現沒有達到VGG16分割結果的效果。

4.2 Combining What and Where

We define a new fully convolutional net for segmentation that combines layers of the feature hierarchy and refines the spatial precision of the output. See Figure. 3.

While fully convolutionalized classifiers fine-tuned to semantic segmentation as shown in Section 4.1, and even score highly on the standard metrics, their output is dissatisfyingly coarse (see Fig. 4). The 32 pixel stride at the final prediction layer limits the scale of detail in the upsampled output.

We address this by adding skips [1] that combine the final prediction layer with lower layers with finer strides. This turns a line topology into a DAG, with edges that skip ahead from lower layers to higher ones (Figure 3). As they see fewer pixels, the finer scale predictions should need fewer layers, so it makes sense to make them from shallower net outputs. Combining fine layers and coarse layers lets the model make local predictions that respect global structure. By analogy to the jet of Koenderick and van Doorn [19], we call our nonlinear feature hierarchy the deep jet.

We first divide the output stride in half by predicting from a 16 pixel stride layer. We add a 1 × 1 convolution layer on top of pool4 to produce additional class predictions. We fuse this output with the predictions computed on top of conv7 (convolutionalized fc7) at stride 32 by adding a 2× upsampling layer and summing6both predictions (see Figure 3). We initialize the 2× upsampling to bilinear inter-polation, but allow the parameters to be learned as described in Section 3.3. Finally, the stride 16 predictions are upsampled back to the image. We call this net FCN-16s. FCN-16s is learned end-to-end, initialized with the parameters of the last, coarser net, which we now call FCN-32s. The new parameters acting on pool4 are zeroinitialized so that the net starts with unmodified predictions. The learning rate is decreased by a factor of 100.

Learning this skip net improves performance on the validation set by 3.0 mean IU to 62.4. Figure 4 shows improvement in the fine structure of the output. We compared this fusion with learning only from the pool4 layer, which resulted in poor performance, and simply decreasing the learning rate without adding the skip, which resulted in an insignificant performance improvement without improving the quality of the output.

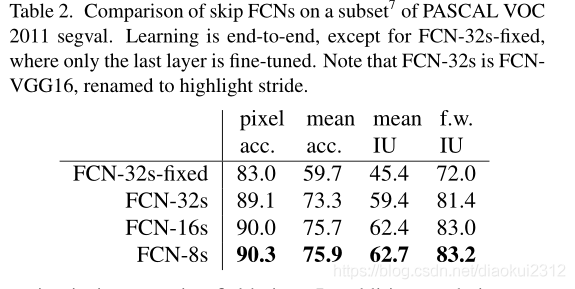
We continue in this fashion by fusing predictions from pool3 with a 2× upsampling of predictions fused from pool4 and conv7, building the net FCN-8s. We obtain a minor additional improvement to 62.7 mean IU, and find a slight improvement in the smoothness and detail of our output. At this point our fusion improvements have met diminishing returns, both with respect to the IU metric which empha-sizes large-scale correctness, and also in terms of the improvement visible e.g. in Figure 4, so we do not continue fusing even lower layers.

Refinement by other means Decreasing the stride of pooling layers is the most straightforward way to obtain finer predictions. However, doing so is problematic for our VGG16-based net. Setting the pool5 stride to 1 requires our convolutionalized fc6 to have kernel size 14 × 14 to maintain its receptive field size. In addition to their computational cost, we had difficulty learning such large filters. We attem-pted to re-architect the layers above pool5 with smaller filters, but did not achieve comparable perfor-mance; one possible explanation is that the ILSVRC initialization of the upper layers is important.

Anotherwaytoobtainfinerpredictionsistousetheshiftand-stitch trick described in Section 3.2. In limited experiments, we found the cost to improvement ratio from this method to be worse than layer fusion.

4.3結合什麼和在哪裏結合

  我們定義了一個用於分割的新的全折積網路，它結合了特徵層次結構的各層，並細化了輸出的空間精度。參見圖3。

  儘管完全折積分類器可以按照如4.1中說明進行微調，甚至這些基礎網路在標準指標上得分很高，但它們的輸出卻令人不盡如人意（見圖4）。最終預測層的32畫素步幅限制了上採樣輸出中的細節尺度。

  我們通過新增跳躍結構[51]來解決此問題，該跳躍結構融合了最終預測層與具有更加精細步幅的較低層。這將線拓撲變成DAG，其邊緣從較低層跳到叫高層（圖3）。因爲他們看到的畫素更少，更精細的尺度預測應該需要更少的層，因此從較淺的網路輸出是有意義的。結合精細層和粗糙層可以讓模型做出符合全域性結構的區域性預測。與肯德爾裡克和範·多恩[19]的覆蓋相似 [19]，我們將非線性特徵層次稱爲深覆蓋。
  我們首先通過從16畫素步幅層進行預測，將輸出步幅分成兩半。我們在pool4的頂部新增了1 × 1折積層，以產生額外的類別預測。我們通過增加一個2倍的上採樣層並將兩個預測相加，將此輸出與在步幅爲32的conv7(折積fc7)上計算的預測相融合(見圖3)。我們將2倍上採樣初始化爲雙線性插值，但允許按照第3.3節所述學習參數。最後，將步幅16預測上採樣回到影象。我們稱這個網路爲FCN-16。FCN-16s是端到端學習的，用最後一個較粗網路的參數初始化，我們現在稱之爲FCN-32s。作用於pool4的新參數被初始化爲零，因此網路從未修改的預測開始。學習率降低了100倍。

  學習這個skip網路可以將驗證集上的效能提高平均IU3.0到62.4。圖4顯示了輸出精細結構的改進。我們將這種融合僅與來自pool4層的學習進行了比較，這導致效能較差，並且僅在不新增跳過的情況下降低了學習速度，從而在不提高輸出品質的情況下導致了微不足道的效能改進。

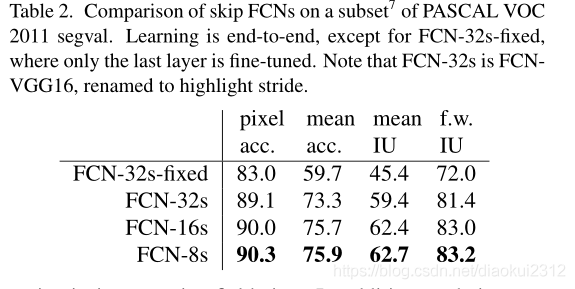
  我們繼續以這種方式將pool3的預測與融合了pool4和conv7的2x上採樣預測相融合，建立網路FCN-8s。我們獲得了一個小的額外改進，平均IU達到62.7，並且我們的輸出的平滑度和細節略有改善。至此，我們的融合改進遇到了收益遞減的問題，無論是在強調大規模正確性的IU度量方面，還是在可見的改進方面，例如，所以在圖4中，我們不會繼續融合更低的層。

通過其他方式進行細化 減少池化層的步幅是獲得更精細預測的最直接方法。但是，這樣做對我們基於VGG16的網路來說是個問題。將pool5層設定爲具有步幅1要求我們的折積化fc6具有14×14的內核大小以便維持其感受野大小。除了計算成本之外，我們還難以學習如此大的過濾器。我們嘗試用較小的過濾器重新構建pool5之上的層，但是沒有成功實現相當的效能；一種可能的解釋是，從上層的ILSVRC初始化很重要。
  獲得更好預測的另一種方法是使用3.2節中描述的shift-and-stitch技巧。在有限的實驗中，我們發現這種方法的改進成本比層融合更差。

4.3 Experimental Framework

Optimization We train by SGD with momentum. We use a minibatch size of 20 images and fixed learning rates of $10^{-3}$, $10^{-4}$, and $5^{-5}$for FCN-AlexNet, FCN-VGG16, and FCN-GoogLeNet, respectively, chosen by line search. We use momentum 0.9, weight decay of $5^{-4}$or $2^{-4}$, and doubled learning rate for biases, although we found training to be sensitive to the learning rate alone. We zero-initialize the class scoring layer, as random initialization yielded neither better performance nor faster convergence. Dropout was included where used in the original classifier nets.
Fine-tuning We fine-tune all layers by backpropagation through the whole net. Fine-tuning the output classifier alone yields only 70% of the full finetuning performance as compared in Table 2. Training from scratch is not feasible considering the time required to learn the base classification nets. (Note that the VGG net is trained in stages, while we initialize from the full 16-layer version.) Fine-tuning takes three days on a single GPU for the coarse FCN-32s version, and about one day each to upgrade to the FCN-16s and FCN-8s versions.

More Training Data The PASCAL VOC 2011 segmentation training set labels 1112 images. Hariharan et al. [14] collected labels for a larger set of 8498 PASCAL training images, which was used to train the previous state-of-theart system, SDS [15]. This training data improves the FCNVGG16 validation score7by 3.4 points to 59.4 mean IU.

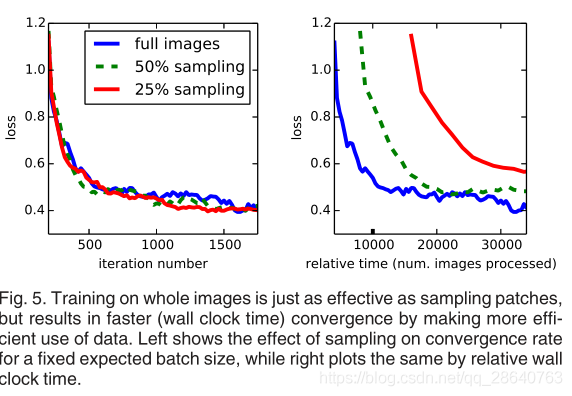
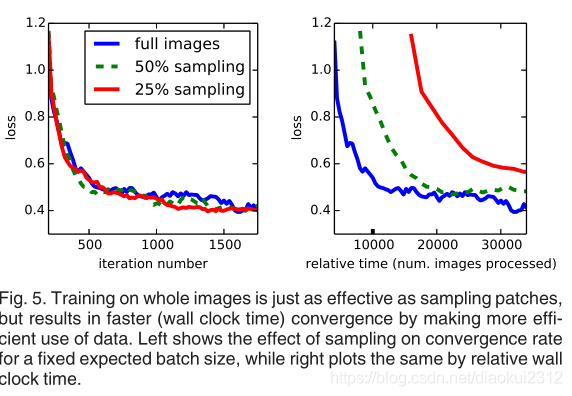
Patch Sampling As explained in Section 3.4, our full image training effectively batches each image into a regular grid of large, overlapping patches. By contrast, prior work randomly samples patches over a full dataset [27, 2, 7, 28, 9], potentially resulting in higher variance batches that may accelerate convergence [22]. We study this tradeoff by spatially sampling the loss in the manner described earlier, making an independent choice to ignore each final layer cell with some probability 1 − p. To avoid changing the effective batch size, we simultaneously increase the number of images per batch by a factor 1/p. Note that due to the efficiency of convolution, this form of rejection sampling is still faster than patchwise training for large enough values of p (e.g., at least for p > 0.2 according to the num-bers in Section 3.1). Figure 5 shows the effect of this form of sampling on convergence. We find that sampling does not have a significant effect on convergence rate compared to whole image training, but takes significantly more time due to the larger number of images that need to be consi-dered per batch. We therefore choose unsampled, whole image training in our other experiments.

Class Balancing Fully convolutional training can balance classes by weighting or sampling the loss. Although our labels are mildly unbalanced (about 3/4 are background), we find class balancing unnecessary.

Dense Prediction The scores are upsampled to the input dimensions by deconvolution layers within the net. Final layer deconvolutional filters are fixed to bilinear interpolation, while intermediate upsampling layers are initialized to bilinear upsampling, and then learned.

Augmentation We tried augmenting the training data by randomly mirroring and 「jittering」 the images by translating them up to 32 pixels (the coarsest scale of prediction) in each direction. This yielded no noticeable improvement.

Implementation All models are trained and tested with Caffe [18] on a single NVIDIA Tesla K40c. Our models and code are publicly available at
http://fcn.berkeleyvision.org.

4.3實驗框架

  優化 我們用帶有動量的隨機梯度下降演算法（SGD）進行訓練。我們使用的mini-batch大小爲20張圖片，和對於FCN-AlexNet, FCN-VGG16和FCN-GoogleNet使用由線性搜尋得到的固定的學習率，分別爲$10^{-3}$, $10^{-4}$, 和 $5^{-5}$。我們使用動量爲0.9，權重衰減爲$5^{-4}$或$2^{-4}$，並且將對偏差的學習率增加了一倍，雖然我們發現訓練僅對學習速率敏感。我們對類評分層進行零初始化，因爲隨機初始化既不能產生更好的效能，也不能更快的收斂。Droupout被包含在原始分類器網路中使用。
  微調 我們通過整個網路的反向傳播來微調所有層。如表2所示，單獨微調輸出分類器僅是完全微調效能的70％。考慮到學習基礎分類網所需的時間，從頭開始訓練是不可行的。 （請注意，VGG網路是分階段訓練的，而我們是從完整的16層版本初始化的。）對於粗FCN-32s版本，單個GPU上的微調需要三天時間，而每個版本大約需要一天時間才能 纔能升級到FCN-16s和FCN-8s版本。

  更多的訓練數據 PASCAL VOC 2011分割訓練集標籤1112張影象。Hariharan等人[14]收集了一組更大的8498 PASCAL訓練影象的標籤，用於訓練之前的先進系統SDS[15]。這一訓練數據提高了FCNVGG16驗證集的分數3.4分，達到平均59.4 IU。

  Patch採樣 如第3.4節所述，我們的整個影象訓練有效地將每個影象分批成一個規則的大重疊網格塊。相比之下，先前的工作在整個數據集上隨機採樣patches，可能導致更高的方差批次，從而可能加速收斂。我們通過以前面描述的方式對損失進行空間採樣來研究這種權衡，並做出獨立選擇，以1-p的概率忽略每個最終層單元。 爲了避免更改有效的批次大小，我們同時將每批次的影象數量增加了1/p。請注意，由於折積效率高，對於足夠大的p值（例如，至少根據第3.1節中的p> 0.2而言），這種形式的拒絕採樣仍比逐塊訓練更快。圖5顯示了這種採樣形式對收斂的影響。我們發現，與整個影象訓練相比，採​​樣對收斂速度沒有顯着影響，但是由於每批需要考慮的影象數量更多，因此採樣花費的時間明顯更多。因此，我們在其他實驗中選擇未採樣的整體影象訓練。

5 Results

We test our FCN on semantic segmentation and scene parsing, exploring PASCAL VOC, NYUDv2, and SIFT Flow. Although these tasks have historically distinguished between objects and regions, we treat both uniformly as pixel prediction. We evaluate our FCN skip architecture on each of these datasets, and then extend it to multi-modal input for NYUDv2 and multi-task prediction for the semantic and geometric labels of SIFT Flow.

Metrics We report four metrics from common semantic segmentation and scene parsing evaluations that are variations on pixel accuracy and region intersection over union (IU). Let $n_{ij}$be the number of pixels of class $i$ predicted to belong to class $j$, where there are $n_{cl}$ different classes, and let $t_i=\sum _{j}n^{_{ij}}$ be the total number of pixels of class $i$. We compute:

• pixel accuracy: $\sum _{i}n^{_{ii}}/\sum _{i}t_{i}$
• mean accuraccy:$\left ( 1/n_{cl} \right )\sum_{i}n^{_{ii}}/t{_{i}}$
• mean IU:$\left ( 1/n_{cl} \right )\sum_{i}n^{_{ii}}/\left ( t{_{i}}+\sum _{j}n_{ji}-n_{ii} \right )$
• frequency weighted IU:$\left ( \sum _{k}t_{k} \right )^{-1}\sum _{i}t_{i}n_{ii}/\left ( t_{i}+\sum _{j}n_{ji}-n_{ii} \right )$

PASCAL VOC. Table 4 gives the performance of our FCN-8s on the test sets of PASCAL VOC 2011 and 2012, and compares it to the previous best, SDS [14], and the well-known R-CNN [5]. We achieve the best results on mean IU by 30 percent relative. Inference time is reduced $114\times$(convnet only, ignoring proposals and refinement) or $286\times$ (overall). Fig. 6 compares the outputs of FCN-8s and SDS.

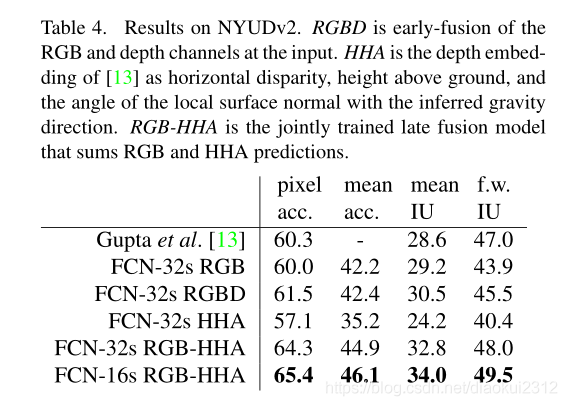
NYUDv2. is an RGB-D dataset collected using the Microsoft Kinect. It has 1,449 RGB-D images, with pixelwise labels that have been coalesced into a 40 class semantic segmentation task by Gupta et al. We report results on the standard split of 795 training images and 654 testing images.(Note: all model selection is performed on PASCAL 2011 val.)Table 4 gives the performance of several net variations. First we train our unmodified coarse model (FCN-32s) on RGB images. To add depth information, we train on a model upgraded to take four-channel RGB-D input (early fusion). This provides little benefit, perhaps due to similar number of parameters or the difficulty of propagating meaningful gradients all the way through the model. Following the success of Gupta et al[13], we try the three-dimensional HHA encoding of depth , training nets on just this information,as well as a 「late fusion」 of RGB and HHA where the predictions from both nets are summed at the final layer, and the resulting two-stream net is learned end-to-end. Finally we upgrade this late fusion net to a 16-stride version.

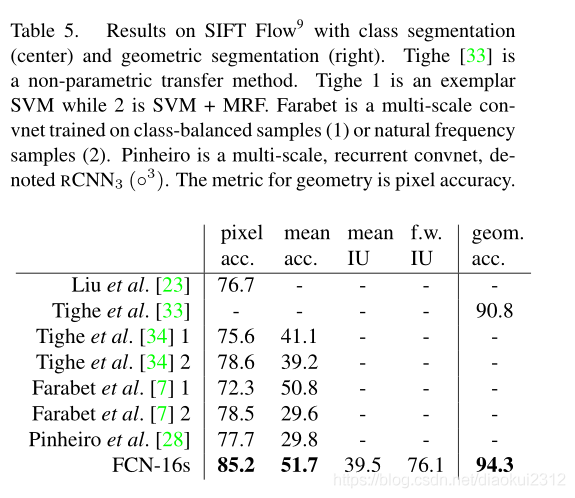
SIFT Flow is a dataset of 2,688 images with pixel labels for 33 semantic classes (「bridge」, 「mountain」, 「sun」), as well as three geometric classes (「horizontal」, 「vertical」, and 「sky」). An FCN can naturally learn a joint representation that simultaneously predicts both types of labels. We learn a two-headed version of FCN-16s with semantic and geometric prediction layers and losses.The learned model performs as well on both tasks as two independently trained models, while learning and inference are essentially as fast as each independent model by itself. The results in Table 5, computed on the standard split into 2,488 training and 200 test images,9show state-of-the-art performance on both tasks.

5 結果

  我們測試了我們的FCN在語意分割和場景解析，探索PASCAL VOC，NYUDv2，和SIFT Flow。 雖然這些任務歷來在物件和區域之間有所區別，但我們將兩者均視爲畫素預測。 我們在每個數據集上評估FCN跳躍體系結構，然後將其擴充套件到NYUDv2的多模式輸入，以及SIFT Flow的語意和幾何標籤的多工預測。
  PASCAL VOC. 表3給出了FCN-8在PASCAL VOC 2011和2012測試集上的效能，並將其與之前的最先進的SDS [15]和著名的R-CNN[10] 進行了比較。我們在平均IU上取得了20%的相對優勢。推理時間減少了114倍（僅限於convnet，忽略提案和完善內容）或286倍（總體）。

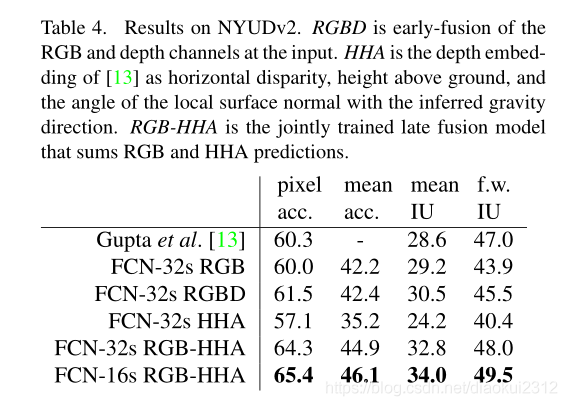
  NYUDv2. 是使用Microsoft Kinect收集的RGB-D數據集。它具有1449個RGB-D影象，帶有按畫素劃分的標籤，由Gupta等人合併爲40類語意分割任務。我們報告了795張訓練影象和654張測試影象的標準分割結果。表4給出了幾種淨變化的效能。首先，我們在RGB影象上訓練未修改的粗糙模型（FCN-32s）。爲了增加深度資訊，我們訓練了一個升級後的模型以採用四通道RGB-D輸入（早期融合）。這可能帶來的好處很小，這可能是由於參數數量相似或難以通過網路傳播有意義的梯度所致。繼成功Gupta等。我們嘗試對深度進行三維HHA編碼，以及後期融合的RGB和HHA都是預測在最終層相加,，並得出結果兩流網路是端到端學習的。最後，我們將這個後期的融合網路升級爲16步版本。

  SIFT流. 是2688個影象的數據集，帶有33個語意類別（「橋」，「山」，「太陽」）以及三個幾何類別（「水平」，「垂直」和「天空」）的畫素標籤。 FCN可以自然地學習可以同時預測兩種標籤型別的聯合表示。我們學習了帶有語意和幾何預測層以及損失的FCN-16s的兩頭版本。該網路在兩個任務上的表現都好於兩個獨立訓練的網路，而學習和推理基本上與每個獨立的網路一樣快。表5中的結果按標準劃分爲2488個訓練影象和200張測試影象，在兩個任務上均顯示出更好的效能。

6 Conclusion

Fully convolutional networks are a rich class of models, of which modern classification convnets are a special case. Recognizing this, extending these classification nets to segmentation, and improving the architecture with multi-resolution layer combinations dramatically improves the state-of-the-art, while simultaneously simplifying and speeding up learning and inference.

Acknowledgements This work was supported in part by DARPA ’s MSEE and SMISC programs, NSF awards IIS1427425, IIS-1212798, IIS-1116411, and the NSF GRFP , Toyota, and the Berkeley Vision and Learning Center. We gratefully acknowledge NVIDIA for GPU donation. We thank Bharath Hariharan and Saurabh Gupta for their advice and dataset tools. We thank Sergio Guadarrama for reproducing GoogLeNet in Caffe. We thank Jitendra Malik for his helpful comments. Thanks to Wei Liu for pointing out an issue wth our SIFT Flow mean IU computation and an error in our frequency weighted mean IU formula.

6 分析

7.參考文獻

References