C語言實現最短路徑問題(Floyd演算法)

本文收此文章啓發：弗洛伊德演算法

需要注意三點
①三個回圈的意義，最外層i是中轉結點，然後內層是求第j個結點通過ii結點做中轉到第k個結點的最短路徑
②路徑的儲存，注意更新的時候需要的是j->i的路徑
③一開始要給有邊的路徑設定名字

PS：如果自己有到自己的路徑 設定的輸出爲路徑的值，但課本輸出0

測試圖片：

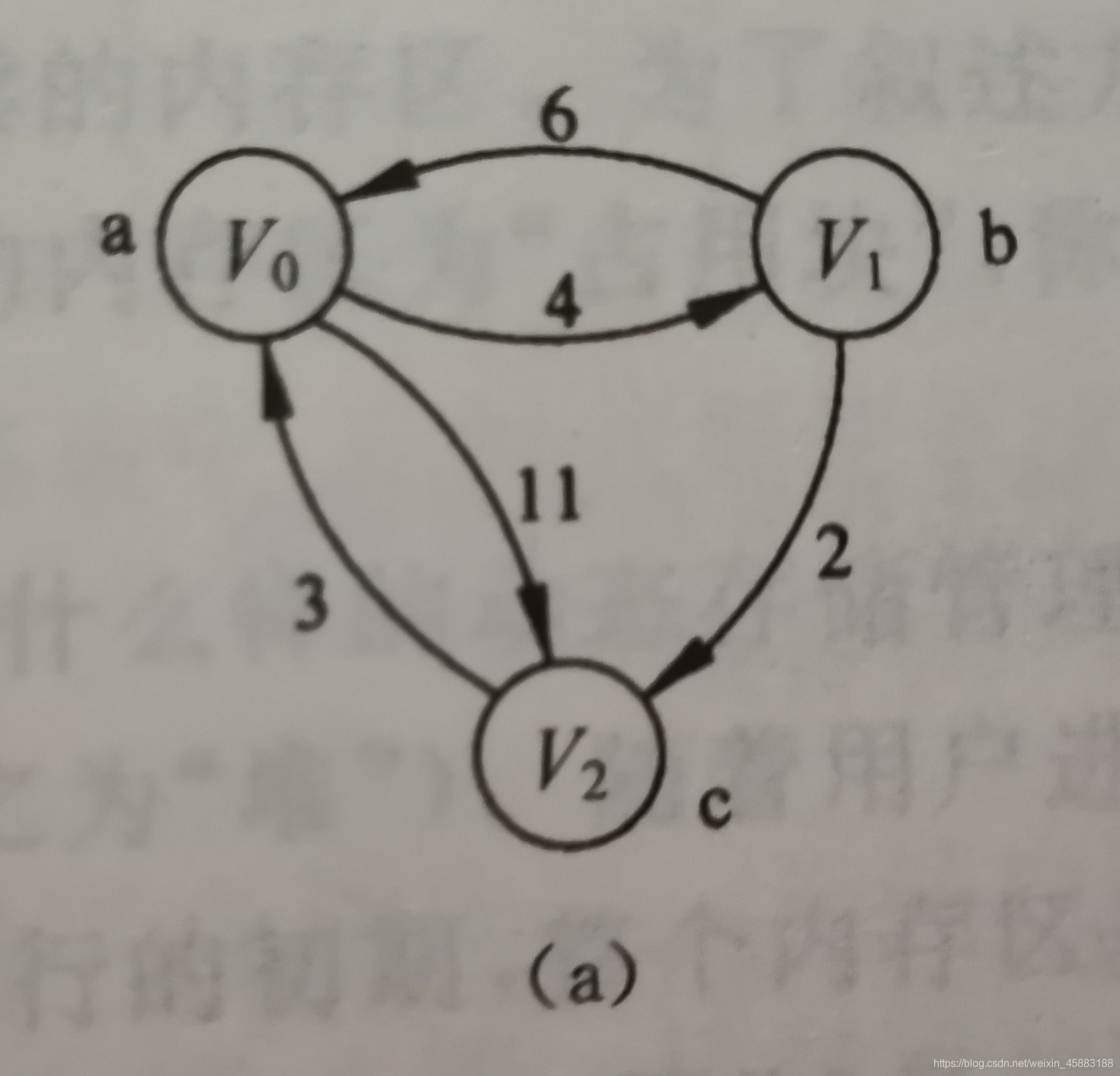
檔案內容：
在這裏插入程式碼片
輸出結果：

程式碼：

/*
	實現內容：Floyd演算法
	VS2019 編譯通過 王大花 2020.8.9
*/

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MaxVexNameLength 2
#define MaxPathLength 30
#define TextPath "C:\\Users\\86132\\Desktop\\最短路徑Floyd\\ALGraph.txt"

//頂點結點
typedef struct _VexNode {
	char Date[MaxVexNameLength + 1];

}VexNode;

typedef struct _Floyd {
	int** Path_Length;
	char*** Path;

}Floyd;

//圖
typedef struct _ALGraph {
	VexNode* Vertics;
	int VexNum, ArcNum;
	int** ArcMatrix;
	Floyd Flo;

}ALGraph;

//找到頂點位置
int Locate(char* ch) {
	return (3 == strlen(ch)) ? 10 * (ch[1] - '0') + ch[2] - '0' : ch[1] - '0';

}

void Creat_ALGraph(ALGraph* G) {

	FILE* fp = fopen(TextPath, "r");
	fscanf(fp, "%d%d", &G->VexNum, &G->ArcNum);

	//讀取頂點資訊 同時初始化鄰接矩陣、路徑矩陣
	G->Vertics = (VexNode*)malloc(sizeof(VexNode) * G->VexNum);
	G->ArcMatrix = (int**)malloc(sizeof(int*) * G->VexNum);
	G->Flo.Path_Length = (int**)malloc(sizeof(int*) * G->VexNum);
	G->Flo.Path = (char***)malloc(sizeof(char**) * G->VexNum);

	for (int i = 0; i < G->VexNum; i++) {
		fscanf(fp, "%s", G->Vertics[i].Date);
		//初始化鄰接矩陣 路徑矩陣
		G->ArcMatrix[i] = (int*)malloc(sizeof(int) * G->VexNum);
		G->Flo.Path_Length[i] = (int*)malloc(sizeof(int) * G->VexNum);
		G->Flo.Path[i] = (char**)malloc(sizeof(char*) * G->VexNum);

		for (int j = 0; j < G->VexNum; j++) {
			G->ArcMatrix[i][j] = INT_MAX;
			G->Flo.Path_Length[i][j] = INT_MAX;
			G->Flo.Path[i][j] = (char*)malloc(sizeof(char) * MaxPathLength);
			memset(G->Flo.Path[i][j], 0, sizeof(char) * MaxPathLength);
		}
	}

	//錄入弧的資訊
	for (int i = 0; i < G->ArcNum; i++) {
		char ch1[MaxVexNameLength + 1], ch2[MaxVexNameLength + 1];
		int tmp;
		fscanf(fp, "%s%s%d", ch1, ch2, &tmp);
		G->ArcMatrix[Locate(ch1)][Locate(ch2)] = tmp;
		G->Flo.Path_Length[Locate(ch1)][Locate(ch2)] = tmp;
	}
	for (int i = 0; i < G->VexNum; i++) {
		for (int j = 0; j < G->VexNum; j++) {
			if (INT_MAX != G->ArcMatrix[i][j]) {
				strcat(G->Flo.Path[i][j], " -> ");
				strcat(G->Flo.Path[i][j], G->Vertics[j].Date);
			}
		}
	}

	fclose(fp);
}

void Shortest_Path_Floyd(ALGraph G) {

	//只讓第i個做中轉站 計算其餘頂點之間的距離
	for (int i = 0; i < G.VexNum; i++) {
		//計算第j個頂點在第i箇中轉站的前提下和k頂點(其餘所有頂點)的距離
		for (int j = 0; j < G.VexNum; j++) {
			for (int k = 0; k < G.VexNum; k++) {

				if (INT_MAX == G.ArcMatrix[j][i] || INT_MAX == G.ArcMatrix[i][k])
					continue;
				if (INT_MAX == G.Flo.Path_Length[j][k] || G.Flo.Path_Length[j][k] > G.ArcMatrix[j][i] + G.ArcMatrix[i][k]) {
					G.Flo.Path_Length[j][k] = G.ArcMatrix[j][i] + G.ArcMatrix[i][k];

					G.Flo.Path[j][k][0] = 0;
					strcat(G.Flo.Path[j][k], G.Flo.Path[j][i]);
					strcat(G.Flo.Path[j][k], " -> ");
					strcat(G.Flo.Path[j][k], G.Vertics[k].Date);
				}
			}
		}
	}
}

void Print_Floyd_Path(ALGraph G) {

	for (int i = 0; i < G.VexNum; i++) {
		for (int j = 0; j < G.VexNum; j++) {
			if (INT_MAX != G.Flo.Path_Length[i][j])
				printf("%s%s\t路徑長度：%d\n", G.Vertics[i].Date, G.Flo.Path[i][j], G.Flo.Path_Length[i][j]);
			else
				printf("%s%s -> %s\t路徑不存在\n", G.Vertics[i].Date, G.Flo.Path[i][j], G.Vertics[j].Date);
		}
	}
}

int main() {

	ALGraph G;
	Creat_ALGraph(&G);
	Shortest_Path_Floyd(G);
	Print_Floyd_Path(G);

	return 0;
}