一、啞變數定義

啞變數（DummyVariable），也叫虛擬變數，引入啞變數的目的是，將不能夠定量處理的變數量化，線上性迴歸分析中引入啞變數的目的是，可以考察定性因素對因變數的影響，它是人爲虛設的變數，通常取值爲0或1，來反映某個變數的不同屬性。對於有n個分類屬性的自變數，通常需要選取1個分類作爲參照，因此可以產生n-1個啞變數。如職業、性別對收入的影響，戰爭、自然災害對GDP的影響，季節對某些產品（如冷飲）銷售的影響等等。這種「量化」通常是通過引入「啞變數」來完成的。根據這些因素的屬性型別，構造只取「0」或「1」的人工變數，通常稱爲啞變數（dummyvariables），記爲D。

舉一個例子，假設變數「職業」的取值分別爲：工人、農民、學生、企業職員、其他，5種選項，我們可以增加4個啞變數來代替「職業」這個變數，分別爲D1（1=工人/0=非工人）、D2(1=農民/0=非農民)、D3（1=學生/0=非學生）、D4(1=企業職員/0=非企業職員)，最後一個選項「其他」的資訊已經包含在這4個變數中了，所以不需要再增加一個D5（1=其他/0=非其他）了。這個過程就是引入啞變數的過程，其實在結合分析（ConjointAnalysis）中，就是利用啞變數來分析各個屬性的效用值的。

此時，我們通常會將原始的多分類變數轉化爲啞變數，每個啞變數只代表某兩個級別或若幹個級別間的差異，通過構建迴歸模型，每一個啞變數都能得出一個估計的迴歸係數，從而使得迴歸的結果更易於解釋，更具有實際意義。

一般的，n個分類需要設定n-1個啞變數（爲什麼不是n個？請繼續看）。

舉個例子，有一個「年齡」變數，分爲：青年，中年，老年三類，那麼我們可以用兩個啞變數來代替：

年齡	變數1	變數2
青年	1	0
中年	0	1
老年	0	0

變數1 = 1代表青年，0代表非青年

變數2 = 1代表中年，0代表非中年

 

變數1和變數2都等於0代表老年

 

所以用2個變數就可以表示3個類別。

 

二、什麼情況下需要設定啞變數

1. 對於無序多分類變數，引入模型時需要轉化爲啞變數

舉一個例子，如血型，一般分爲A、B、O、AB四個型別，爲無序多分類變數，通常情況下在錄入數據的時候，爲了使數據量化，我們常會將其賦值爲1、2、3、4。

從數位的角度來看，賦值爲1、2、3、4後，它們是具有從小到大一定的順序關係的，而實際上，四種血型之間並沒有這種大小關係存在，它們之間應該是相互平等獨立的關係。如果按照1、2、3、4賦值並帶入到迴歸模型中是不合理的，此時我們就需要將其轉化爲啞變數。

2. 對於有序多分類變數，引入模型時需要酌情考慮

例如疾病的嚴重程度，一般分爲輕、中、重度，可認爲是有序多分類變數，通常情況下我們也常會將其賦值爲1、2、3（等距）或1、2、4（等比）等形式，通過由小到大的數位關係，來體現疾病嚴重程度之間一定的等級關係。

但需要注意的是，一旦賦值爲上述等距或等比的數值形式，這在某種程度上是認爲疾病的嚴重程度也呈現類似的等距或等比的關係。而事實上由於疾病在臨牀上的複雜性，不同的嚴重程度之間並非是嚴格的等距或等比關係，因此再賦值爲上述形式就顯得不太合理，此時可以將其轉化爲啞變數進行量化。

3. 對於連續性變數，進行變數轉化時可以考慮設定爲啞變數

對於連續性變數，很多人認爲可以直接將其帶入到迴歸模型中即可，但有時我們還需要結合實際的臨牀意義，對連續性變數作適當的轉換。例如年齡，以連續性變數帶入模型時，其解釋爲年齡每增加一歲時對於因變數的影響。但往往年齡增加一歲，其效應是很微弱的，並沒有太大的實際意義。

此時，我們可以將年齡這個連續性變數進行離散化，按照10歲一個年齡段進行劃分，如0-10、11-20、21-30、31-40等等，將每一組賦值爲1、2、3、4，此時構建模型的迴歸係數就可以解釋爲年齡每增加10歲時對因變數的影響。

以上賦值方式是基於一個前提，即年齡與因變數之間存在着一定的線性關係。但有時候可能會出現以下情況，例如在年齡段較低和較高的人羣中，某種疾病的死亡率較高，而在中青年人羣中，死亡率卻相對較低，年齡和死亡結局之間呈現一個U字型的關係，此時再將年齡段賦值爲1、2、3、4就顯得不太合理了。

因此，當我們無法確定自變數和因變數之間的變化關係，將連續性自變數離散化時，可以考慮進行啞變數轉換。

還有一種情況，例如將BMI按照臨牀診斷標準分爲體重過低、正常體重、超重、肥胖等幾種分類時，由於不同分類之間劃分的切點是不等距的，此時賦值爲1、2、3就不太符合實際情況，也可以考慮將其轉化爲啞變數。

三、如何選擇啞變數的參照組

在上面的內容中我們提到，對於有n個分類的自變數，需要產生n-1個啞變數，當所有n-1個啞變數取值都爲0的時候，這就是該變數的第n類屬性，即我們將這類屬性作爲參照。

例如上面提到的以職業因素爲例，共分爲學生、農民、工人、公務員、其他共5個分類，設定了4啞變數，其中職業因素中「其它」這個屬性，每個啞變數的賦值均爲0，此時我們就將「其它」這個屬性作爲參照，在最後進行模型解釋時，所有類別啞變數的迴歸係數，均表示該啞變數與參照相比之後對因變數的影響。

在設定啞變數時，應該選擇哪一類作爲參照呢？

1. 一般情況下，可以選擇有特定意義的，或者有一定順序水平的類別作爲參照

例如，婚姻狀態分爲未婚、已婚、離異、喪偶等情況，可以將「未婚」作爲參照；或者如學歷 學曆，分爲小學、中學、大學、研究生等類別，存在着一定的順序，可以將「小學」作爲參照，以便於迴歸係數更容易解釋。

2. 可以選擇臨牀正常水平作爲參照

例如，BMI按照臨牀診斷標準分爲體重過低、正常體重、超重、肥胖等類別，此時可以選擇「正常體重」作爲參照，其他分類都與正常體重進行比較，更具有臨牀實際意義。

3. 還可以將研究者所關注的重點類別作爲參照

例如血型，分爲A、B、O、AB四個型別，研究者更關注O型血的人，因此可以將O型作爲參照，來分析其他血型與O型相比後對於結局產生影響的差異。

 四、One-hot encoding（與Dummy Coding對比）

在機器學習問題中，我們通過訓練數據集學習得到的其實就是一組模型的參數，然後通過學習得到的參數確定模型的表示，最後用這個模型再去進行我們後續的預測分類等工作。在模型訓練過程中，我們會對訓練數據集進行抽象、抽取大量特徵，這些特徵中有離散型特徵也有連續型特徵。若此時你使用的模型是簡單模型（如LR），那麼通常我們會對連續型特徵進行離散化操作，然後再對離散的特徵，進行one-hot編碼或啞變數編碼。這樣的操作通常會使得我們模型具有較強的非線效能力。那麼這兩種編碼方式是如何進行的呢？它們之間是否有聯繫？又有什麼樣的區別？是如何提升模型的非線效能力的呢？

• 做啞變數編碼的庫：pandas
• one-hot編碼的庫：sklearn、keras

 4.1 one-hot的基本思想

one-hot的基本思想：將離散型特徵的每一種取值都看成一種狀態，若你的這一特徵中有N個不相同的取值，那麼我們就可以將該特徵抽象成N種不同的狀態，one-hot編碼保證了每一個取值只會使得一種狀態處於「啓用態」，也就是說這N種狀態中只有一個狀態位值爲1，其他狀態位都是0。舉個例子，假設我們以學歷 學曆爲例，我們想要研究的類別爲小學、中學、大學、碩士、博士五種類別，我們使用one-hot對其編碼就會得到：

 

4.2 sklearn進行one-hot編碼

sklearn中有用OneHotEncoder()進行one-hot編碼，但是由於sklearn只處理數值型類別變數，在編碼前需要先將字串轉化爲數值型，用 LabelEncoder函數：

from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OneHotEncoder  
    
label = preprocessing.LabelEncoder()
factory_label = label.fit_transform(factory) 
print(factory_label)  
# 輸出結果  
[[5]
 [3]
 [1]
 [3]
 [6]
 [7]
 [0]
 [0]
 [2]
 [4]]  

 然後再進行one-hot編碼：

# 將行轉列
factory_label = factory_label.reshape(len(factory_label), 1)
# 編碼
factory_encoder = OneHotEncoder(sparse=False)
onehot_encoded = factory_encoder.fit_transform(factory_label)
# 檢視編碼結果
onehot_encoded

Out[53]: 
array([[0., 0., 0., 0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 1., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 0., 0., 0., 1.],
       [1., 0., 0., 0., 0., 0., 0., 0.],
       [1., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 1., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 1., 0., 0., 0.]])

4.3keras進行one-hot編碼

與OneHotEncoder()一樣，再進行one-hot編碼前也需要用 LabelEncoder()先將字串轉化爲數值型。

# 基於keras的onehot編碼 
from keras.utils import to_categorical
from sklearn.preprocessing import LabelEncoder
# str型別轉換
label = LabelEncoder()
factory_label = label.fit_transform(factory)

# 編碼
categorical_encoded = to_categorical(factory_label)
categorical_encoded

Out[85]: 
array([[0., 0., 0., 0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 1., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 0., 0., 0., 1.],
       [1., 0., 0., 0., 0., 0., 0., 0.],
       [1., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 1., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 1., 0., 0., 0.]], dtype=float32)

還可以對one-hot編碼後的數據解碼回去： 

# 解碼
import numpy as np
decode = []
for i in range(len(factory_label)):
    decode.append(np.argmax(categorical_encoded[i]))
print(decode)
# 結果
[5, 3, 1, 3, 6, 7, 0, 0, 2, 4]   

• 對應的原始列表 

index	factory	label
0	C10235	5
1	C10135	3
2	C10035	1
3	C10135	3
4	C10385	6
5	C14534	7
6	**	0
7	**	0
8	C10129	2
9	C10150	4

4.4啞變數編碼

啞變數編碼直觀的解釋就是任意的將一個狀態位去除。還是拿上面的例子來說，我們用4個狀態位就足夠反應上述5個類別的資訊，也就是我們僅僅使用前四個狀態位 [0,0,0,0] 就可以表達博士了。只是因爲對於一個我們研究的樣本，他已不是小學生、也不是中學生、也不是大學生、又不是研究生，那麼我們就可以預設他是博士，是不是。（額，當然他現實生活也可能上幼兒園，但是我們統計的樣本中他並不是，^-^）。所以，我們用啞變數編碼可以將上述5類表示成：

 

4.5 pandas進行啞變數編碼 

pandas中提供了get_dummies()函數：

• pandas.get_dummies(prefix=) prefix參數設定編碼後的變數名，也可以選擇預設

# 匯入數據
import pandas as pd
file = open('D:/myCode/spark/Test/data.csv',encoding='utf-8')
factory = pd.read_csv(file,engine='python')

 數據如下：

Out[1]: 
0    C10235
1    C10135
2    C10035
3    C10135
4    C10385
5    C14534
6        **
7        **
8    C10129
9    C10150
Name: factory_id, dtype: object

 進行啞變數編碼:

encode = pd.get_dummies(factory)

編碼結果（部分展示）:

Out[2]: 
      **  C10035  C10129  C10135  C10150  C10235  C10385  C14534
0   0       0                0            0            0             1            0            0
1   0       0                0            1            0             0            0            0
2   0       1                0            0            0             0            0            0
3   0       0                0            1            0             0            0            0
4   0       0                0            0            0             0            1            0
5   0       0                0            0            0             0            0            1
6   1       0                0            0            0             0            0            0
7   1       0                0            0            0             0            0            0
8   0       0                1            0            0             0            0            0
9   0       0                0            0            1             0            0            0

說明

get_dummies可以對多列（字元型和數值型）直接進行啞變數編碼
缺點：如果在測試集中出現了訓練集沒有出現過的型別，簡單的用get_dummies會出現錯誤，比如訓練集中的性別是男、女，而在測試集中有男、女、未知這三種類型的特徵出現，直接用get_dummies處理的話兩個數據集生成的啞變數特徵數不一致。 

4.6 One-hot編碼和Dummy編碼：區別與聯繫 

• One-Hot編碼和啞變數編碼都只能對離散型變數進行編碼。
• One-Hot編碼之後生成的新特徵數等於對應特徵的不同種類取值個數，feature1中共有3種不同的取值，One-Hot編碼之後生成的新特徵數就是3。而啞變數編碼之後生成的新特徵數比對應特徵的取值個數少1個。
• One-Hot編碼之所以叫One-Hot編碼，是因爲每個取值對應的編碼中有且只有一個是1，其餘都是0。而啞變數編碼允許不出現1。
• One-Hot編碼形成的新特徵都是二值型特徵，比如，上述One-Hot編碼形成的三個新維度的意義爲：feature1是否爲3，feature1是否爲2，feature1是否爲1；啞變數編碼在這一點上與One-Hot類似，只不過當編碼全爲0是表示 feature1既不是1也不是2，這種情況下預設feature1爲3。

通過上面的例子，我們可以看出它們的「思想路線」是相同的，只是啞變數編碼覺得one-hot編碼太羅嗦了（一些很明顯的事實還說的這麼清楚），所以它就很那麼很明顯的東西省去了。這種簡化不能說到底好不好，這要看使用的場景。下面 下麪我們以一個例子來說明：

　　假設我們現在獲得了一個模型，這裏自變數滿足（因爲特徵是one-hot獲得的，所有隻有一個狀態位爲1，其他都爲了0，所以它們加和總是等於1），故我們可以用表示第三個特徵，將其帶入模型中，得到：

　　　　　

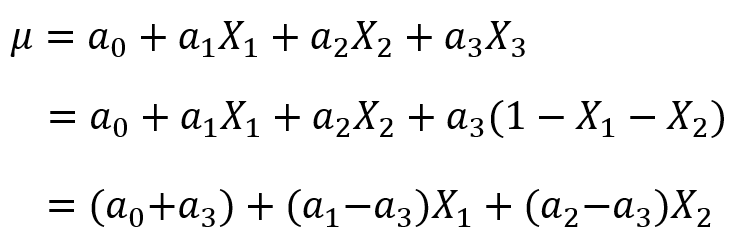
這時，我們就驚奇的發現和這兩個參數是等價的！那麼我們模型的穩定性就成了一個待解決的問題。這個問題這麼解決呢？有三種方法：

（1）使用正則化手段，將參數的選擇上加一個限制，就是選擇參數元素值小的那個作爲最終參數，這樣我們得到的參數就唯一了，模型也就穩定了。

（2）把偏置項去掉，這時我們發現也可以解決同一個模型參數等價的問題。

　　　　

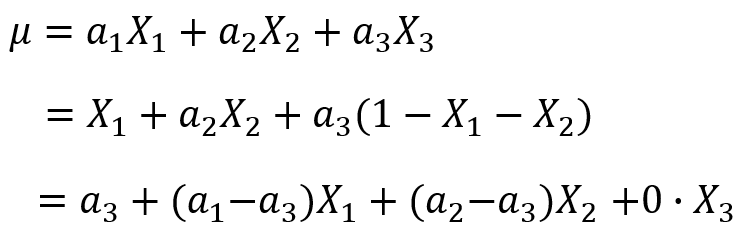
　　因爲有了bias項，所以和我們去掉bias項的模型是完全不同的模型，不存在參數等價的問題。

（3）再加上bias項的前提下，使用啞變數編碼代替one-hot編碼，這時去除了，也就不存在之前一種特徵可以用其他特徵表示的問題了。

總結：我們使用one-hot編碼時，通常我們的模型不加bias項 或者 加上bias項然後使用正則化手段去約束參數；當我們使用啞變數編碼時，通常我們的模型都會加bias項，因爲不加bias項會導致固有屬性的丟失。

選擇建議：我感覺最好是選擇正則化 + one-hot編碼；啞變數編碼也可以使用，不過最好選擇前者。雖然啞變數可以去除one-hot編碼的冗餘資訊，但是因爲每個離散型特徵各個取值的地位都是對等的，隨意取捨未免來的太隨意。

4.7 連續值的離散化爲什麼會提升模型的非線效能力 

簡單的說，使用連續變數的LR模型，模型表示爲公式（1），而使用了one-hot或啞變數編碼後的模型表示爲公式（2）

　　　　　

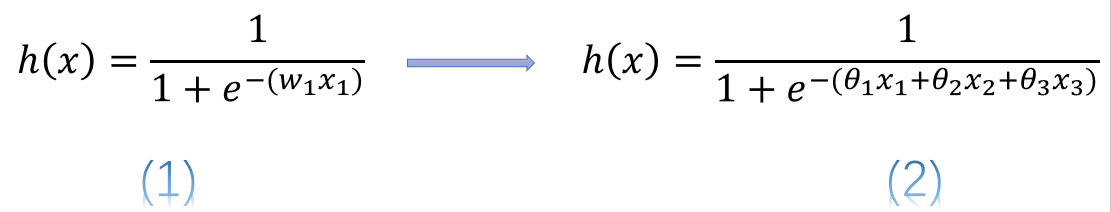
式中表示連續型特徵，、、分別是離散化後在使用one-hot或啞變數編碼後的若幹個特徵表示。這時我們發現使用連續值的LR模型用一個權值去管理該特徵，而one-hot後有三個權值管理了這個特徵，這樣使得參數管理的更加精細，所以這樣拓展了LR模型的非線效能力。

　　這樣做除了增強了模型的非線效能力外，還有什麼好處呢？這樣做了我們至少不用再去對變數進行歸一化，也可以加速參數的更新速度；再者使得一個很大權值管理一個特徵，拆分成了許多小的權值管理這個特徵多個表示，這樣做降低了特徵值擾動對模型爲穩定性影響，也降低了異常數據對模型的影響，進而使得模型具有更好的魯棒性。

注：參考文章地址：https://www.cnblogs.com/lianyingteng/p/7792693.html