前端學數據結構與演算法(二):陣列與棧
前言
數據結構與演算法有相互依存的關係,如果將這個兩個又進行劃分,無疑數據結構又是這座大廈的基礎。首先從線性數據結構開始,介紹大家耳熟能詳的數據結構-陣列。因爲JavaScript已經爲陣列封裝了很多增刪改查以及遍歷的方法,這裏就不再贅述具體API了。而後半部分將使用陣列實現一種受限的數據結構-棧。最後會解題幾道leetCode上與棧相關的題目,方便更加深入理解這種受限數據結構的用途。
陣列特性
重溫一下上一章複雜度分析最後留下的一個範例,它的時間複雜度是多少:
function test(arr) {
let len = arr.length
for (let i = 0; i < len; i++) {
arr.shift()
}
}
通過上一章的知識點,我們很容易知道,一層回圈嘛。那就是O(n)複雜度,但這裏並非如此,複雜度應是O(n²),至於爲什麼,首先從陣列的特性開始說起。
陣列的定義
從百度百科裏陣列的定義,可以瞭解陣列主要有以下特性:
- 儲存多個相同類型的集合
- 長度固定
- 佔用連續的儲存空間
但是在JavaScript中,陣列的特性基本都不符合以上三條。首先可以存放JavaScript裡任意不同的數據到同一個數組裏;然後長度是可以動態擴容的;最後絕大部分情況下確實是佔用連續的儲存空間,但如果是以下情況:
const arr = ['a', 'b']
arr[10000] = 'c'
JavaScript中不會去開闢這麼大的連續的記憶體,僅僅儲存這3個變數,而是使用雜湊表(雜湊表)這種數據結構去儲存,這樣的話佔用的記憶體雖然不是連續的,但是節約了儲存空間,不過因爲存取的key需要通過雜湊函數轉次手,所以存取效率會低於連續儲存的陣列。JavaScript裡的陣列爲何與其他語言的相差這麼多,僅僅是因爲是在傳統陣列上進行了再一次的底層封裝,才讓其使用這麼靈活。
陣列的增刪查
一般考量一個數據結構的效能,主要從增刪查三個基本操作分別考量,因爲改你只需要查到這個元素即可。不同場景下的這幾種基本操作頻率的不同,從而也決定了使用哪種數據結構更爲高效。
增
往數組裏增加元素,不同的位置時間複雜度並不相同,我們分別來分析首位、中間部位、尾部三種情況。例如我在數據的首位增加一條數據:
const arr = [1, 2, 3, 4];
arr.unshift(0)
原陣列會變成[0, 1, 2, 3, 4],原來陣列的第一位變爲新插入的元素,舊數據整體向後移動一位,所以時間複雜度是O(n);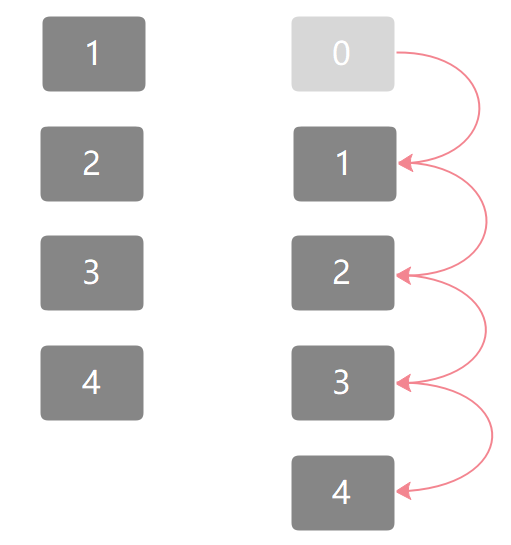
從中間部位插入元素時,插入之前的元素不用移位,但是之後的元素還是需要整體後移,所以時間複雜度依然還是O(n);但如果是從陣列的最後插入元素時,前面所有的元素都不需要移動,陣列末尾新增一個元素即可,所以時間複雜度是O(1)。
刪
從上面增加元素的表現可以看出來,陣列的特性是,只要裏面的元素位置會發生變動,就需要搬家這個操作,所以刪除操作依然如此。只要不是刪除的最後一個元素,其他位置元素的刪除都需要O(n)複雜度,如果是刪除最後一個元素,那一樣只需要O(1)。
再看本章開頭的那段範例,即使是隻使用一層的回圈,也可以理解爲什麼時間複雜度依然會是O(n²),這是陣列的特性決定的。而shift方法也只是封裝的方法,該方法在其內部會執行O(n)的操作。
function test(arr) {
let len = arr.length
for (let i = 0; i < len; i++) {
arr.shift() // 每一次操作都需要整體搬家
}
}
查
陣列最重要的特性,那就是根據下標存取陣列內的元素,無論是任何位置,時間複雜度都是O(1)。當然如果你需要存取到對應某個值,還是需要O(n)的複雜度去遍歷。
我們對陣列操作API做了簡單瞭解,隨機存取是陣列的優勢,或僅僅在陣列的末尾增加與刪除操作也是O(1)的操作,其他情況都是O(n)的複雜度。
受限的數據結構-棧
可以把棧想象成是疊盤子這個行爲,當我們開始摞的時候是放在之前盤子的上面,而取的時候是從最上面的盤子開始拿。棧是一種遵從後進先出的有序數據集合,一頭堵死,最先進入棧的元素,最後出棧。
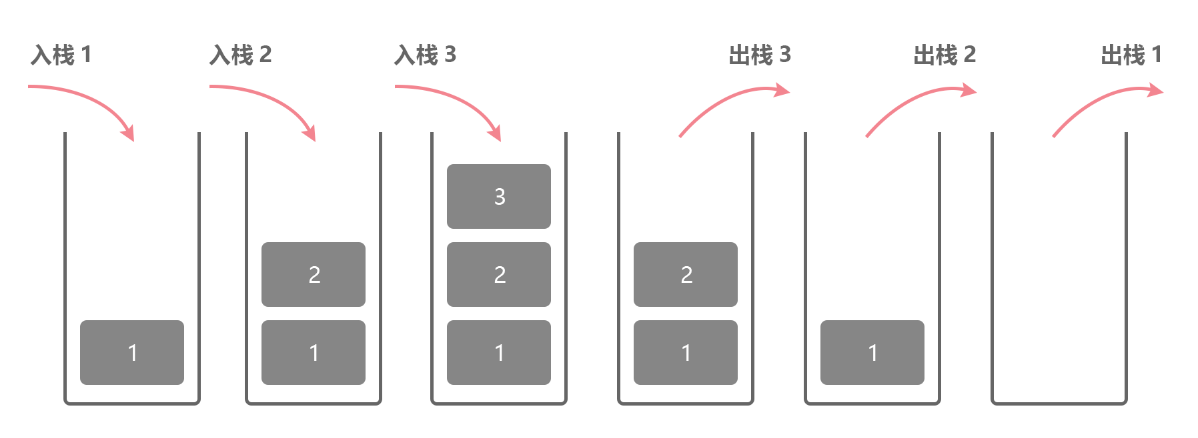
對上面數組的增刪查分析我們知道,在陣列的最後一位進行增加與刪除都是O(1)的複雜度,所以非常適合用來實現棧這種數據結構。其實完全可以把陣列當棧使用,但實現棧的目的就是爲了只暴露少量的介面供外面使用,防止有中間的過多操作。我們用陣列來實現一個棧:
class Stack {
constructor() {
this._data = []
}
push(e) {
this._data.push(e)
}
pop() {
return this._data.pop()
}
size() {
return this._data.length
}
}
實現棧的方式不僅僅只有陣列,用物件也沒問題,只不過陣列有封裝好的對應方法,用其他方式需要自己手寫push和pop操作而已。
LeetCode解題
正是由於棧的受限,往往再處理特定問題時,邏輯會更清晰。
20.有效的括號 ↓
給定一個只包括 '(',')','{','}','[',']' 的字串,判斷字串是否有效。
有效字串需滿足:
1. 左括號必須用相同類型的右括號閉合。
2. 左括號必須以正確的順序閉合。
範例:
"()[]{}" // true
"([)]" // false
"{[]}" // true
這是一個使用棧解決的經典的問題:思路就是建立一個棧,遇到左括號時就入棧,遇到右括號時就彈出棧頂元素,看當前的括號是否與彈出的匹配,只要有一次不匹配,就返回false,最後檢查該棧是否爲空即可。
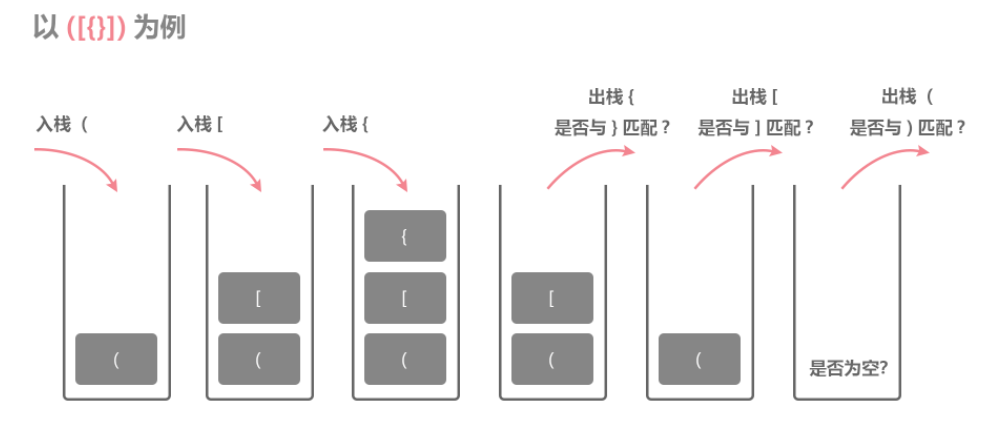
程式碼如下:
var isValid = function (s) {
const leftBrackets = '([{'
const brackets = {
')': '(',
']': '[',
'}': '{'
}
const stack = new Stack()
for (const c of s) {
if (leftBrackets.indexOf(c) > -1) {
stack.push(c) // 左括號就入棧
} else {
const d = stack.pop() // 彈出棧頂元素
if (d !== brackets[c]) { // 是否匹配
return false
}
}
}
return stack.size() === 0 // 是否爲空
};
71.簡化路徑 ↓
以Unix風格給出一個檔案的絕對路徑,將其轉換爲規範路徑。
一個點(.)表示當前目錄本身;
此外,兩個點(..)表示將目錄切換到上一級(指向父目錄);
兩者都可以是複雜相對路徑的組成部分。
請注意,返回的規範路徑必須始終以斜槓 / 開頭,並且兩個目錄名之間必須只有一個斜槓 /。
最後一個目錄名(如果存在)不能以 / 結尾。此外,規範路徑必須是表示絕對路徑的最短字串。
範例:
輸入:"/a/./b/../../c/"
輸出:"/c"
輸入:"/a/../../b/../c//.//"
輸出:"/c"
輸入:"/a//b////c/d//././/.."
輸出:"/a/b/c"
解題思路:首先使用split按照/進行路徑分割,因爲兩個目錄之間的多個/只能有一個斜槓,這樣多個連續/被分割後,中間存在的只是空字串,而空字串和.對當前的目錄路徑沒有影響,只有遇到..會返回上一級的目錄,依然使用棧解決。
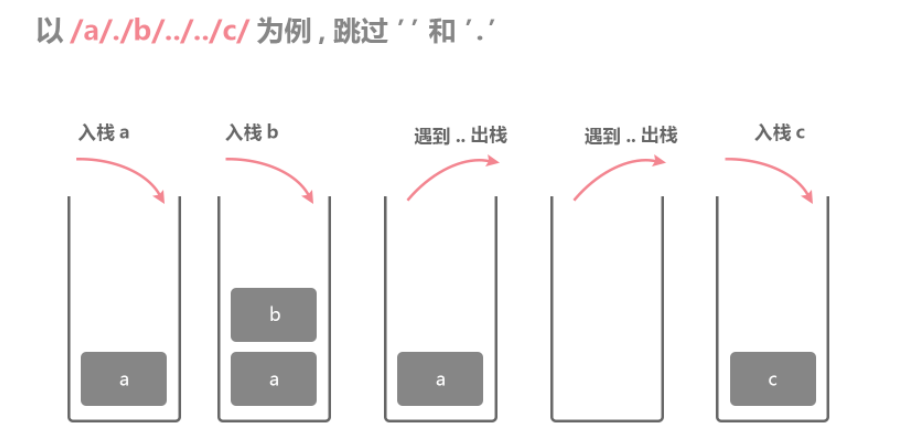
程式碼如下:
var simplifyPath = function (path) {
const stack = new Stack() // 新增join方法
const pathArr = path.split('/')
for (const s of pathArr) {
if (s === '' || s === '.') {
continue;
} else if (s === '..') {
stack.pop()
} else {
stack.push(s)
}
}
return '/' + stack.join('/')
};
150.逆波蘭表達式求值 ↓
有效的運算子包括 +, -, *, / 。每個運算物件可以是整數,也可以是另一個逆波蘭表達式,求表達式的值。
範例:
輸入: ["4", "13", "5", "/", "+"]
輸出: 6
解釋: 該算式轉化爲常見的中綴算術表達式爲:(4 + (13 / 5)) = 6
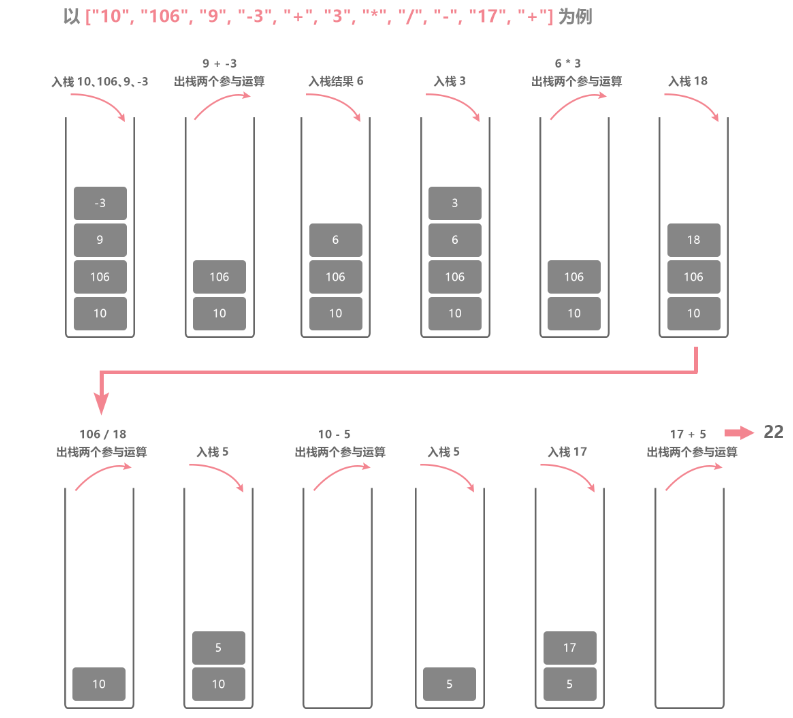
輸入: ["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"]
輸出: 22
解釋:
該算式轉化爲常見的中綴算術表達式爲:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
解題思路:觀察這個轉換表達式求值運算的過程可以發現,沒有*或/優先順序高於+和-這麼一說,只是根據運算子出現先後順序計算。所以我們依然建立一個棧,只要遇到的是數位就壓入棧,如果遇到運算子就從棧裡彈出兩個數位參與運算,將運算的結果再一次壓入棧內即可,直到表達式全部運算完成。
程式碼如下:
const SIGN = {
'*': (a, b) => a * b,
'/': (a, b) => a / b | 0, // 向下取整
'+': (a, b) => a + b,
'-': (a, b) => a - b
}
var evalRPN = function(tokens) {
const stack = new Stack()
tokens.forEach(item => {
if (item in SIGN) { // 是運算子
const b = stack.pop()
const a = stack.pop() // 彈出兩個
const res = SIGN[item](a, b)
stack.push(res) // 結果再壓入棧
} else {
stack.push(+item) // 是數位直接壓入棧
}
})
return stack.pop()
};
理解棧這種陣列結構非常重要,後續的章節還會探討遞回相關的問題,而遞回的實現也就是呼叫了系統的函數呼叫棧;同樣理解陣列的增刪查原理也很重要,它能讓我們避免陷入以爲程式碼越短效率越高的陷阱,因爲增刪查的API只是JavaScript替我們封裝的而已,很多操作內部依然是O(n)。
最後
還是留一個題目,這個題目不是力扣上的,可以挑戰下,如下:
計算字串表達式的值:
"3+8*5-6/3" // 41
"1+2*2-6+8/2*3-4" // 7
提示:
使用兩個棧
大家也能看出,這是一個系列文章,個人也爲這個系列文章開源了一個github倉庫,會更加完整的收錄文章內的程式碼與力扣題解,以及最後題目的題解,同時也會不定期編寫力扣題解豐富這個倉庫,歡迎大家收錄。