摘要

神經機器翻譯（NMT）是一種用於自動翻譯的端到端學習方法，具有克服傳統基於短語的翻譯系統的許多弱點的潛力。不幸的是，衆所周知，NMT系統在訓練和翻譯推理方面在計算上都是昂貴的–在非常大的數據集和大型模型的情況下，有時會令人望而卻步。一些研究人員還指控NMT系統缺乏魯棒性，特別是當輸入句子包含稀有單詞時。這些問題阻礙了NMT在實際部署和服務中的使用，這些部署和服務中準確性和速度都至關重要的。在這項工作中，我們介紹了GNMT，即Google的神經機器翻譯系統，該系統試圖解決其中的許多問題。我們的模型包括一系列深度LSTM網路，該網路具有8個編碼器和8個解碼器層，使用殘差連線以及從解碼器網路到編碼器的注意力連線。爲了提高並行度並因此減少訓練時間，我們的注意力機制 機製將解碼器的底層連線到編碼器的頂層。爲了加快最終翻譯速度，我們在推理計算過程中採用了低精度演算法。爲了改善對稀有單詞的處理，我們將單詞分爲有限的一組公共子詞單元（wordpieces）集合，用於輸入和輸出。這種方法在「字元」級模型的靈活性與「單詞」級模型的效率之間取得了良好的平衡，自然地處理了稀有單詞的翻譯，並最終提高了系統的整體準確性。我們的集束搜尋技術採用長度歸一化方法並使用覆蓋率懲罰，這會鼓勵生成最有可能覆蓋源句子中所有單詞的輸出句子。爲了直接優化翻譯BLEU分數，我們考慮使用強化學習來完善模型，但是我們發現BLEU分數的提高並未反映在人工評估中。在WMT’14的英語到法語和英語到德語的基準測試中，GNMT取得了最好的測試結果。與一組基於短語的生成系統相比，通過對一組孤立的簡單句子進行人工並排評估，可將翻譯錯誤平均減少60％。

1.介紹

神經機器翻譯（NMT）最近被引入作爲一種有效的方法，有可能解決傳統機器翻譯系統的許多缺點。NMT的優勢在於它能夠以端到端的方式直接學習從輸入文字到關聯的輸出文字的對映的能力。它的體系結構通常由兩個回圈神經網路（RNN）組成，一個用於獲取輸入文字序列，另一個用於生成翻譯的輸出文字。NMT通常伴隨着注意力機制 機製，該機制 機製可以幫助它有效地應對較長的輸入序列。
　　神經機器翻譯的一個優點是它避免了傳統的基於短語的機器翻譯中許多脆弱的設計選擇。然而，實際上，NMT系統過去的準確性要比基於短語的翻譯系統差，特別是在針對非常好的公共翻譯系統所使用的超大規模數據集進行訓練時。
　　神經機器翻譯的三個固有弱點是造成這種差距的原因：
　　（1）訓練速度和推理速度較慢；
　　（2）處理稀有單詞的效率低下；
　　（3）有時無法翻譯源句子中的所有單詞。
　　首先，在大規模翻譯數據集上訓練NMT系統通常需要花費大量時間和計算資源，從而減慢了實驗週轉時間和創新的速度。在翻譯推理時，由於使用了大量參數，它們通常比基於短語的系統慢得多。其次，NMT在翻譯稀有單詞方面缺乏魯棒性。儘管原則上可以通過訓練「複製模型」來模仿傳統的對齊模型來解決，或通過使用注意力機制 機製來複制稀有詞來解決，但由於對齊品質因語言而異，這些方法在大規模上都不可靠，並且當網路較深時，由注意力機制 機製產生的潛在對齊方式是不穩定的。同樣，簡單複製可能並不總是應付稀有字詞的最佳策略，例如在音譯更合適的情況下。最後，NMT系統有時會產生無法翻譯輸入句子所有部分的輸出句子，換句話說，它們無法完全「覆蓋」輸入內容，這可能導致令人詫異的翻譯結果。
　　這項工作介紹了GNMT的設計和實現，這是Google提供的NMT系統，旨在爲上述問題提供解決方案。在我們的實現中，回圈網路是長短期記憶（LSTM）RNN 。我們的LSTM RNN具有8層，各層之間具殘差連線以加速梯度傳播。對於並行性，我們將注意力從解碼器網路的底層連線到編碼器網路的頂層。爲了縮短推理時間，我們採用了低精度的推理演算法，並通過特殊硬體（Google的Tensor Processing Unit，即TPU）進一步加快了推理速度。爲了有效處理稀有單詞，我們在系統中使用子詞單元（也稱爲「wordpieces」）作爲輸入和輸出。使用wordpieces可以在單個字元的靈活性和完整單詞的解碼效率之間取得良好的平衡，並且也避免了對未知字詞進行特殊處理的需求。我們的集束搜尋技術包括一個長度歸一化過程，可以有效地處理在解碼過程中比較不同長度的假設的問題，另外，我們還提供了一個覆蓋損失，可以鼓勵模型覆蓋所有提供的輸入。
　　我們的實現是健壯的，並且在許多語言對之間的一系列數據集上表現良好，而無需進行特定於語言的調整。使用相同的實現，我們獲得的結果可以與標準基準上的最新技術相媲美或優於以前的最新系統，同時對Google的基於短語的生成翻譯系統進行了重大改進。具體而言，在WMT’14英語到法語中，我們的單個模型得分爲38.95 BLEU，比[31]中報告的沒有外部對齊模型的單個模型得分高了7.5 BLEU，而比[45]中報告的與沒有外部對齊模型的單個模型得分則爲高了1.2 BLEU。我們的單個模型也可以與[45]中的單個模型進行比較，而沒有像[45]中那樣使用任何對齊模型。同樣，在WMT’14英語到德語的比賽中，我們的單個模型得分爲24.17 BLEU，比以前的基準高3.4 BLEU。在生產數據上，我們的實施更加有效。人工評估顯示，與我們先前基於短語的系統相比，GNMT在許多語言對上的翻譯錯誤減少了60％：英語↔法語，英語↔西班牙語和英語↔中文。其他實驗表明，最終翻譯系統的品質已接近普通譯員的品質。

2.相關工作

統計機器翻譯（SMT）幾十年來一直是主要的翻譯方法。SMT的實現通常是基於短語的機器翻譯系統（PBMT），該系統翻譯長度不同的單詞或短語序列。
　　甚至在神經機器翻譯問世之前，神經網路已被用作SMT系統中的元件，並取得了一些成功。 也許最引人注目的嘗試之一是使用聯合語言模型來學習短語表示，當與基於短語的翻譯結合使用時，這產生了很大的改進。但是，這種方法仍然以基於短語的翻譯系統爲核心，因此繼承了它們的缺點。其他所提出的學習短語表示或使用神經網路學習端到端翻譯的方法提供了較好的結果，但與基於短語的系統相比，最終的總體準確性較差。
　　過去的研究人員已經嘗試了用於機器翻譯的端到端學習的概念，但收效甚微。在該領域的開創性論文[41，2]之後，NMT的翻譯品質已逐漸接近傳統研究基準的基於短語的翻譯系統的水平。可能在[31]中描述了超過基於短語的翻譯的首次成功嘗試。與最新的基於詞組的系統相比，該系統在WMT’14英譯法上實現了0.5 BLEU的改進。
　　從那以後，已經提出了許多新技術來進一步改善NMT：使用注意力機制 機製處理稀有詞，爲翻譯覆蓋率建模的機制 機製，多工和半監督訓練以合併更多數據，字元解碼器，字元編碼器，處理稀有詞輸出的子詞單元，不同種類的注意機制 機製和句子級最小化損失。儘管這些系統的翻譯準確性令人鼓舞，但仍缺乏與大規模，基於短語的翻譯系統的系統性比較。

3.模型結構

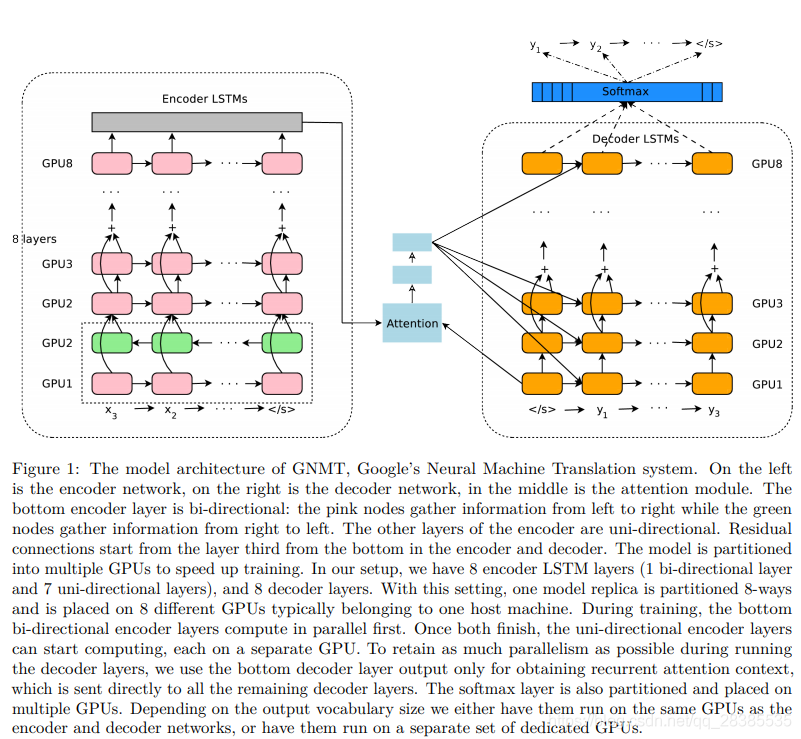
　　我們的模型（見圖1）遵循傳統的序列到序列學習框架，並引入注意力機制 機製。它具有三個組成部分：a.編碼器網路，b.解碼器網路和c.注意力網路。編碼器將源語句轉換爲向量列表，每個輸入符號輸出一個向量。 給定此向量列表，解碼器一次生成一個符號，直到生成特殊的句子結束符號（EOS）。 編碼器和解碼器通過注意力模組連線，該模組允許解碼器在解碼過程中專注於源語句的不同區域。
　　對於所使用的符號，我們使用粗體小寫字母表示向量（例如$\pmb v,\pmb o_i$），使用粗體大寫字母表示矩陣（例如$\pmb U,\pmb W$），使用草書大寫字母表示集合（例如$\mathcal V,\mathcal T$），使用大寫字母表示表示序列（例如$X,Y$），小寫字母表示序列中的各個符號（例如$x_1,x_2$）。
　　令$(X,Y)$爲源句和目標句對。 令$X=x_1,x_2,x_3,...,x_M$是源句子中$M$個符號的序列，而$Y=y_1,y_2,y_3,...,y_N$是目標句子中$N$個符號的序列。編碼器只是以下形式的函數：
$\pmb x_1,\pmb x_2,\dots,\pmb x_M=EncoderRNN(x_1,x_2,x_3,\dots,x_M)\tag{1}$
在此等式中，$\pmb x_1,\pmb x_2,\dots,\pmb x_M$是固定向量維度的列表。列表中的成員數與源句子中的符號數相同（在此範例中爲$M$）。使用鏈式規則，可以將序列$P(Y|X)$的條件概率分解爲：
$P(Y|X)=P(Y|\pmb x_1,\pmb x_2,\dots,\pmb x_M)=\prod^N_{i=1}P(y_i|y_0,y_1,y_2,...,y_{i-1};\pmb x_1,\pmb x_2,\dots,\pmb x_M)\tag{2}$
其中$y_0$是用於表示「句子開頭」的特殊符號，位於每個目標句子之前。
　　在推理過程中，我們計算到目前爲止給定源句編碼和已解碼目標序列的下一個符號的概率：
$P(y_i|y_0,y_1,y_2,...,y_{i-1};\pmb x_1,\pmb x_2,\dots,\pmb x_M)\tag{3}$
　　我們的解碼器實現爲RNN網路和softmax層的組合。解碼器RNN網路爲要預測的下一個符號生成隱藏狀態$\pmb y_i$，然後將其通過softmax層以在候選輸出符號上生成概率分佈。
　　在我們的實驗中，我們發現，要使NMT系統達到良好的精度，編碼器和解碼器RNN都必須足夠深，以捕獲源語言和目標語言中的細微不規則性。這種觀測結果與以前的相似，即深LSTM明顯優於淺LSTM。在這項工作中，每個額外的層將困惑度降低了近10％。與[31]相似，我們對編碼器RNN和解碼器RNN都使用了深度堆疊的長短期記憶（LSTM）網路。
　　我們的注意力模組類似於[2]。更具體地說，令$\pmb y_{i-1}$爲上一時刻的解碼器-RNN輸出。當前時刻的注意上下文$\pmb a_i$根據以下公式計算：
$s_t=AttentionFunction(\pmb y_{i-1},\pmb x_t)\quad \forall t,\quad 1\le t \le M$
$p_t=exp(s_t)/\sum^M_{t=1}exp(s_t)\quad \forall t,\quad 1\le t \le M \tag{4}$
$\pmb a_i=\sum^M_{t=1}p_t\pmb x_t$
其中，我們實現的AttentionFunction是具有一個隱藏層的前饋網路。

3.1 殘差鏈接

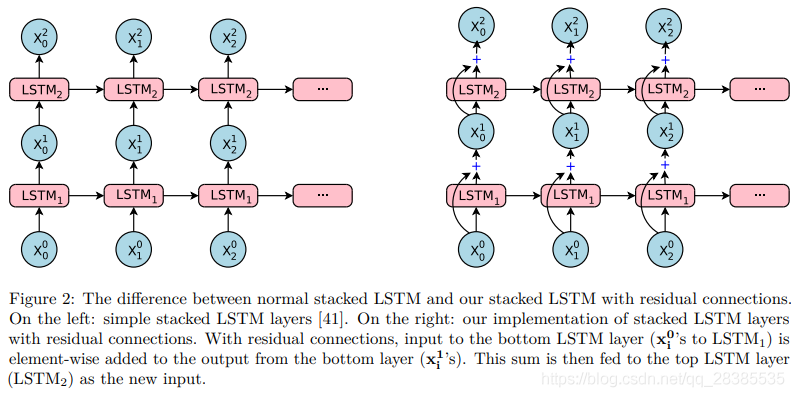
　　如上所述，與淺層模型相比，較深的LSTM通常會提供更高的精度。然而，簡單地堆疊更多的LSTM層只能在一定數量的層上起作用，超過這些層，網路變得太慢且難以訓練，這可能是由於梯度爆炸和梯度消失問題引起的。根據我們在大規模翻譯任務方面的經驗，簡單的堆疊LSTM層可以很好地工作到4層，極限只有6層，而超過8層則會導致非常差的效能。
　　出於對中間層的輸出和目標之間的差異進行建模的想法的推動，這種想法在過去的論文中已顯示對許多工都適用，我們在堆疊中的LSTM層之間引入了殘差連線（請參見圖2）。更具體地，令$LSTM_i$和$LSTM_{i+1}$爲堆疊中的第$i$個和第$i+1$個LSTM層，其參數分別爲$\pmb W_i$和$\pmb W_{i+1}$。在第$t$步，對於沒有殘留連線的堆疊LSTM，我們有：
$\pmb c^i_t,\pmb m^i_t=LSTM_i(\pmb c^i_{t-1}, \pmb m^i_{t-1},\pmb x^{i-1}_t;\pmb W^i)$
$\pmb x^i_t=\pmb m^i_t\tag{5}$
$\pmb c^{i+1}_t,\pmb m^{i+1}_t=LSTM_{i+1}(\pmb c^{i+1}_{t-1}, \pmb m^{i+1}_{t-1},\pmb x^{i}_t;\pmb W^{i+1})$
其中$x^{i-1}_t$是在時刻$t$處$LSTM_i$的輸入，而$m^i_t$和$c^i_t$分別是在時刻$t$處$LSTM_i$的隱藏狀態和記憶狀態。
　　在$LSTM_i$和$LSTM_{i+1}$之間存在殘差鏈接的情況下，上述公式變爲：
$\pmb c^i_t,\pmb m^i_t=LSTM_i(\pmb c^i_{t-1}, \pmb m^i_{t-1},\pmb x^{i-1}_t;\pmb W^i)$
$\pmb x^i_t=\pmb m^i_t+\pmb x^{i-1}_t\tag{6}$
$\pmb c^{i+1}_t,\pmb m^{i+1}_t=LSTM_{i+1}(\pmb c^{i+1}_{t-1}, \pmb m^{i+1}_{t-1},\pmb x^{i}_t;\pmb W^{i+1})$
殘留連線極大地改善了反向梯度傳播，這使我們能夠訓練非常深的編碼器和解碼器網路。在我們的大多數實驗中，我們使用8個LSTM層作爲編碼器和解碼器，儘管殘差連線可以使我們訓練更深的網路（類似於[45]中觀察到的網路）。

3.2 對於第一層的雙向編碼器

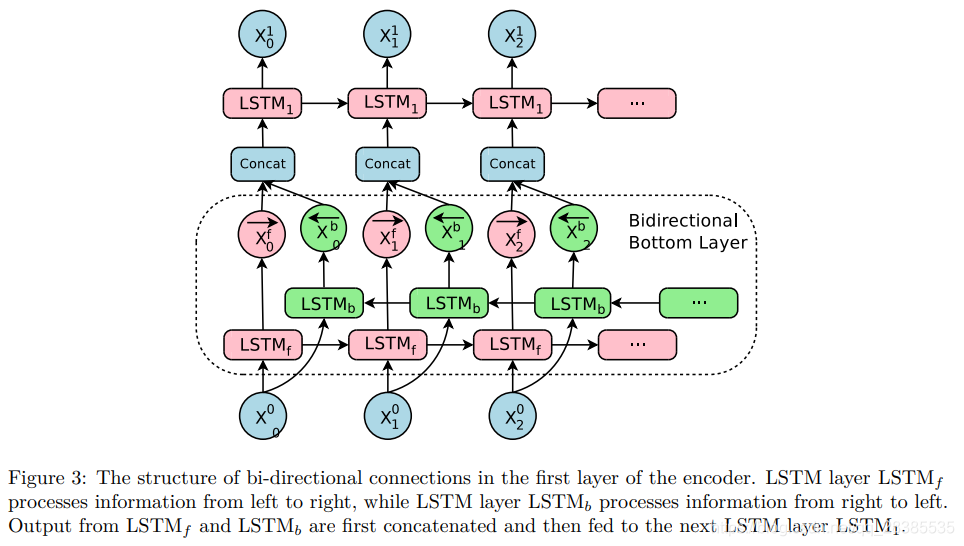
　　對於翻譯系統，在輸出端翻譯某些單詞所需的資訊可以出現在源端的任何位置。通常，源端的資訊是類似於目標端從左到右的，但是取決於語言對，一個具體輸出單詞的資訊能夠被分配甚至拆分到輸入端的某個區域。
　　爲了能在編碼器網路的每個位置都獲得最佳的上下文，對編碼器使用雙向RNN是有意義的，在[2]中也使用了雙向RNN。另外，爲了在計算過程中最大程度地實現並行化（將在第3.3節中進行詳細討論），雙向連線僅用於底部編碼器層-所有其他編碼器層均爲單向的。 圖3說明了我們在底部編碼器層使用雙向LSTM的情況。$LSTM_f$層從左到右處理源語句，$LSTM_b$層則是從右到左處理。來自$LSTM_f(\overrightarrow{\pmb x}^f_t)$和$LSTM_b(\overleftarrow{\pmb x}^b_t)$的輸出首先需要串聯起來，然後才饋送到下一層$LSTM_1$。

3.3 模型並行

由於模型的複雜性，我們同時使用模型並行和數據並行來加快訓練速度。
　　（1）數據並行
　　數據並行很簡單：我們使用Downpour SGD演算法同時訓練$n$個模型副本。$n$個副本都共用一個模型參數，每個副本使用Adam和SGD演算法的組合非同步更新參數。在我們的實驗中，$n$通常約爲10。每個副本一次處理$m$個句子對的mini-batch，在我們的實驗中通常爲$128$。
　　（2）模型並行
　　除數據並行外，模型並行還用於提高每個副本上梯度計算的速度。 編碼器和解碼器網路沿深度方向劃分，並放置在多個GPU上，從而有效地在不同GPU上執行每一層。由於除第一個編碼器層以外的所有層都是單向的，因此第$i+1$層可以在第$i$層完全完成之前開始其計算，從而提高了訓練速度。softmax層也被分割區，每個分割區負責輸出詞彙表中符號的子集。圖1顯示瞭如何完成分割區的更多細節。
　　模型並行對我們可以使用的模型架構施加了某些約束。例如，我們不能爲所有編碼器層都設定雙向LSTM層，因爲這樣做會降低後續層之間的並行度，因爲每一層都必須等待，直到前一層的正反兩個方向都完成爲止。這將有效地限制我們僅並行使用2個GPU（一個用於前向，一個用於後向）。對於模型的注意力部分，我們選擇將底部解碼器輸出與頂部編碼器輸出對齊，以在執行解碼器網路時最大程度地提高並行度。如果我們將頂部解碼器層與頂部編碼器層對齊，我們將消除解碼器網路中的所有並行性，並且不會受益於使用多個GPU進行解碼。

4.分段方法

即使翻譯從根本上來說是一個開放的詞彙問題（名稱，數位，日期等），但是神經機器翻譯模型也經常使用固定的單詞詞彙進行操作。解決未登錄（OOV）單詞的方法有兩大類。一種方法是根據注意力模型，使用外部對齊模型，簡單地將稀有詞從源複製到目標（因爲最稀有詞是名稱或數位，而正確的翻譯只是副本）。甚至使用更復雜的專用指向網路。另一類廣泛使用的方法是使用子詞單元，例如字元，詞/字元的混合或更好的子詞。

4.1 wordpiece

我們最成功的方法屬於第二類（子詞單元），並且我們採用最初爲解決Google語音識別系統的日語/韓語分割問題而開發的wordpiece模型（WPM）實現。這種方法完全由數據驅動，並保證爲任何可能的字元序列生成確定性分段。它類似於[38]中處理神經機器翻譯中稀有詞的方法。
　　爲了處理任意單詞，我們首先根據訓練好的wordpiece模型將單詞分解爲wordpiece。在訓練模型之前新增特殊的單詞邊界符號，以便可以從單詞序列中恢復原始單詞序列而不會產生歧義。在解碼時，模型首先生成一個wordpiece序列，然後將其轉換爲相應的word序列。
　　這是一個word序列和相應的wordpiece序列的範例：

• Word: Jet makers feud over seat width with big orders at stake
• wordpieces: _J et _makers _fe ud _over _seat _width _with _big _orders _at _stak

在以上範例中，單詞「Jet」被分解爲兩個單詞「_J」和「et」，單詞「feud」被分解爲兩個單詞「_fe」和「ud」。其他單詞保持爲單個單詞。「 _」是新增的特殊字元，用於標記單詞的開頭。
　　給定一個不斷髮展的單詞定義，使用數據驅動的方法來生成wordpiece模型，以使訓練數據的語言模型概率最大化。給定一個訓練語料和多個所需的字元D，最佳化問題是選擇D個單詞，使得當根據所選wordpiece模型進行分段時，所得語料的單詞數最小。我們針對此優化問題的貪婪演算法類似於[38]，並在[35]中進行了更詳細的描述。與[35]中使用的原始實現相比，我們僅在單詞的開頭而不是兩端使用特殊符號。我們還根據數據將基本字元的數量減少到一個可控的數量（西方語言大約爲500，亞洲語言更多），並將其餘對映到一個特殊的未知字元，以避免用非常稀有的字元污染給定的單詞詞彙。我們發現，使用8k到32k個字詞的總詞彙量可以在我們嘗試過的所有語言對之間達到良好的準確性（BLEU分數）和並或得快速的解碼速度。
　　如上所述，在翻譯中，將稀有實體名稱或數位直接從源複製到目標通常很有意義。爲了促進這種直接複製，我們始終對源語言和目標語言都使用共用的Wordpieces模型。使用這種方法，可以確保以完全相同的方式對源句子和目標句子中的相同字串進行分段，從而使系統更輕鬆地學習複製這些字元。
　　Wordpieces在字元的靈活性和單詞的效率之間取得了平衡。我們還發現，使用wordpieces時，我們的模型在BLEU上獲得了更好的總體評分-可能是由於我們的模型現在可以有效地處理本質上無限的詞彙，而無需求助於字元。後者會使輸入和輸出序列的平均長度更長，因此需要更多的計算。

4.2 詞/字元的混合

我們使用的第二種方法是詞/字元的混合模型。就像在單詞模型中一樣，我們保留固定大小的單詞詞彙。但是，與將OOV單詞摺疊爲單個UNK符號的常規單詞模型不同，我們將OOV單詞轉換爲其組成字元的序列。字元前面帶有特殊的字首，其中1）顯示字元在單詞中的位置，2）在詞彙字元中將它們與普通字元區分開。有三個字首：，和，分別表示單詞的開頭，單詞的中間和單詞的結尾。例如，假設詞彙中沒有單詞Miki。它將被預處理爲一系列特殊標記： M i k i。該過程在源句子和目標句子上都進行實現。在解碼期間，輸出還可能包含特殊字元序列。使用字首，在將字元反轉爲原始單詞時很簡單。

5.訓練準則

給定包含N個輸入-輸出序列對的並行文字數據集，表示爲$\mathcal D≡\{(X^{(i)},Y^{∗(i)})\}^N_{i=1}$，標準的最大似然訓練旨在給定輸入的情況下，最大化真值輸出的對數概率，
$\mathcal O_{ML}(\theta)=\sum^N_{i=1}log~P_{\theta}(Y^{∗(i)}|X^{(i)}).\tag{7}$
這個目標函數的主要問題是它不能反映翻譯中BLEU分數所衡量的任務獎賞函數。此外，該目標函數並不明確鼓勵在不正確的輸出序列之間進行排名，即在模型中，具有較高BLEU分數的輸出仍應在模型中獲得較高的概率，但是在訓練期間從未觀察到不正確的輸出。換句話說，僅使用最大似然訓練，該模型將不會學習到解碼過程中產生錯誤的魯棒性，因爲它們從未被觀察到，這在訓練和測試過程之間是相當不匹配的。
　　最近的幾篇論文考慮了將任務獎賞納入神經序列到序列模型優化的不同方法。在這項工作中，我們還嘗試完善針對最大似然目標進行預訓練的模型，以直接針對任務獎賞進行優化。我們表明，即使在大型數據集上，使用任務獎賞對最新的最大似然模型進行細化也可以顯着改善結果。
　　我們考慮使用期望獎賞目標函數對模型進行細化，可以表示爲：
$\mathcal O_{RL}(\theta)=\sum^N_{i=1}\sum_{Y\in{\mathcal Y }}log~P_{\theta}(Y|X^{(i)})r(Y,Y^{∗(i)}).\tag{8}$
在這裏，$r(Y,Y^{∗(i)})$表示句子分數，並且我們正在計算所有輸出句子$Y$的期望值，直到一定長度。
　　當用於單句時，BLEU評分具有一些不良的特性，因爲它被設計爲語料量度。因此，我們在RL實驗中使用的分數略有不同，我們稱之爲「 GLEU分數」。對於GLEU分數，我們在輸出和目標序列中記錄1、2、3或4個字元的所有子序列（n-gram）。 然後，我們計算召回率（即目標序列中匹配的n-gram數量與總n-gram數量的比率）以及精度（即匹配的n-gram數量的比率）。 那麼GLEU分數就是召回率和精確度的最小值。GLEU分數的範圍始終在0（不匹配）和1（所有匹配）之間，並且在切換輸出和目標時對稱。根據我們的實驗，GLEU分數在語料庫水平上與BLEU指標具有很好的相關性，但是對於我們的每句話獎賞函數沒有缺點。
　　按照強化學習的慣例，我們從等式8中的$r(Y,Y^{∗(i)})$中減去平均獎賞。該平均值估計爲獨立於分佈$P_θ(Y|X^{(i)})$得到的$m$個序列的樣本平均值。在我們的實現中，$m$設定爲15。爲進一步穩定訓練，我們優化ML（方程7）和RL（方程8）目標的線性組合，如下所示：
$\mathcal O_{Mixed}(\theta)=\alpha ∗ O_{ML}(\theta)+\mathcal O_{RL}(\theta)\tag{9}$
在我們的實現中，α通常設定爲0.017。
　　在我們的設定中，我們首先使用最大似然目標（等式7）訓練模型，直到收斂爲止。然後，我們使用混合的最大似然和期望獎賞函數（等式9）細化此模型，直到開發集的BLEU分數不再提高。其中第二步是可選的。

6.量化模型和量化推理

將我們的神經機器翻譯模型部署到我們的互動式產品翻譯服務中的主要挑戰之一是推理上的計算量很大，難以進行低延遲的翻譯，並且大量部署的計算量很大。使用降低精度的方法進行量化推理是一種可以顯着降低這些模型推理成本的技術，通常可以在同一計算裝置上提高效率。例如，在[43]中，證明了在ILSVRC-12基準上，在保證分類精度損失最小的情況下，折積神經網路模型可以以4-6的倍數加速。在[27]中，證明了神經網路模型權重只能量化爲-1、0和+1這三個狀態。
　　然而，許多先前的研究[19、20、43、27]大多集中在具有相對較少層的CNN模型上。具有長序列的深度LSTM提出了一個新的挑戰，因爲在許多次的回圈計算之後或經過深度LSTM堆疊後，量化誤差會顯着放大。
　　在本節中，我們介紹了使用量化演算法加快推理速度的方法。我們的解決方案是針對Google提供的硬體選項量身定製的。爲了減少量化誤差，在訓練過程中保證對模型輸出的影響最小的情況下，向我們的模型新增了其他約束，以便可以量化該模型。也就是說，一旦使用這些附加約束訓練了模型，就可以隨後對其進行量化而不會損失翻譯品質。我們的實驗結果表明，這些附加約束不會影響模型收斂能力，也不會影響模型的品質。
　　根據等式6可知，在帶有殘差連線的LSTM堆疊中，有兩個累加器：沿時間軸的$\pmb c^i_t$和沿深度軸的$\pmb x^i_t$。從理論上講，這兩個累加器都是不受限制的，但實際上，我們注意到它們的值仍然很小。對於量化推理，我們明確地將這些累加器的值限制在$[-δ,δ]$以內，以確保可以在以後特定範圍內進行量化。具有殘差連線的LSTM堆疊的正向計算被修改爲以下內容：
$\pmb c'^i_t,\pmb m^i_t=LSTM_i(\pmb c^i_{t-1},\pmb m^i_{t-1},\pmb x^{i-1}_t;\pmb W^i)$
$\pmb c^i_t=max(-\sigma, min(\sigma, \pmb c'^i_t))$
$\pmb x'^i_t=\pmb m^i_t+\pmb x^{i-1}_t \tag{10}$
$\pmb x^i_t=max(-\sigma, min(\sigma, \pmb x'^i_t))$
$\pmb c'^{i+1}_t,\pmb m^{i+1}_t=LSTM_{i+1}(\pmb c^{i+1}_{t-1},\pmb m^{i+1}_{t-1},\pmb x^{i}_t;\pmb W^{i+1})$
$\pmb c^{i+1}_t=max(-\sigma, min(\sigma, \pmb c'^{i+1}_t))$
　　讓我們在等式10中擴充套件$LSTM_i$以展示內部門控邏輯。爲簡便起見，我們刪除所有上標$i$。

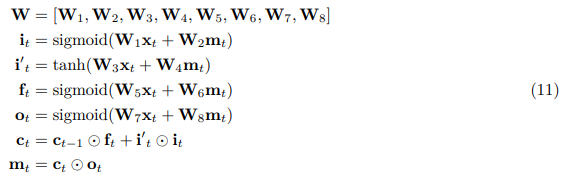
　　在進行量化推理時，我們將等式10和11中的所有浮點運算都替換爲具有8位元或16位元解析度的定點整數運算。上面的權重矩陣$\pmb W$使用8位元整數矩陣$\pmb{WQ}$和浮點向量$\pmb s$表示，如下所示：
$\pmb s_i=nax(abs(\pmb W[i,:]))\\ \pmb{WQ}[i,j]=round(\pmb W[i,j]/\pmb s_i\times 127.0)\tag{12}$
　　所有累加器值（$\pmb c^i_t$和$x^i_t$）都使用範圍$[-δ,δ]$內的16位元整數表示。公式11中的所有矩陣乘法（例如，$\pmb W_1\pmb x_t$，$\pmb W_2\pmb m_t$等）是使用累加到較大累加器中的8位元整數乘法完成的。所有其他操作（包括所有啓用（Sigmoid，tanh）和逐元素操作（$\odot$，$+$））均使用16位元整數操作完成。
　　現在，我們將注意力轉向對數線性softmax層。在訓練期間，給定解碼器RNN網路輸出$\pmb y_t$，我們如下所示計算所有候選輸出符號上的概率向量$\pmb p_t$：
$\pmb v_t=\pmb W_s*\pmb y_t\\ \pmb v'_t=max(-\gamma, min(\gamma, \pmb v_t))\\ \pmb p_t=softmax(\pmb v'_t)\tag{13}$
在等式13中，$\pmb W_s$是線性層的權重矩陣，其具有與目標詞彙表中的符號數相同的行數，並且每一行對應於一個唯一的目標符號。$\pmb v$表示原始logit，將其首先裁剪到$-γ$和$γ$之間，然後歸一化爲概率向量$\pmb p$。由於我們應用於解碼器RNN的量化方案，輸入$\pmb y_t$保證在$-δ$和$δ$之間。logit $\pmb v$的限幅範圍$γ$憑經驗確定，在本例中爲25。在量化推理中，權重矩陣$\pmb W_s$量化爲8位元，如公式12所示，矩陣乘法使用8位元算術。在推理過程中，不會對softmax函數和注意力模型內的計算進行量化。

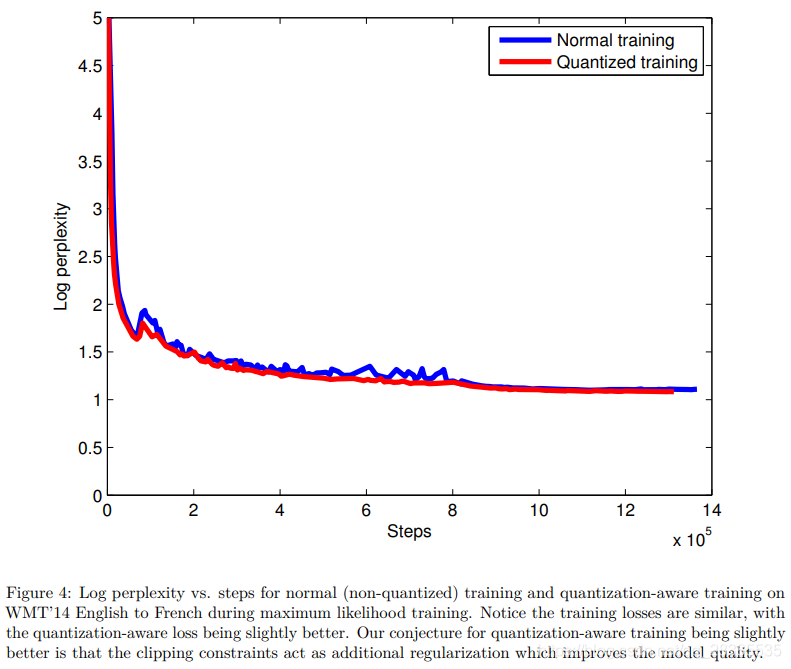
　　值得強調的是，在訓練模型期間，我們使用了全精度浮點數。我們在訓練期間新增到模型的唯一約束是將RNN累加器值裁剪爲$[-δ,δ]$和softmax logits裁剪爲$[-γ,γ]$。$γ$固定爲25.0，而$δ$的值從訓練開始時從$δ= 8.0$的大範圍逐漸退火，直到訓練結束時達到$δ= 1.0$。在推理時，$δ$固定爲1.0。這些附加約束不會降低模型收斂性，也不會降低模型收斂後的解碼品質。在圖4中，我們比較了WMT’14英法文中不受約束的模型（藍色曲線）和受約束的模型（紅色曲線）的損失與迭代步數的關係。我們可以看到，約束模型的損失要好一些，這可能是由於這些約束髮揮的正則化作用。
　　我們的解決方案在效率和準確性之間取得了很好的平衡。由於使用8位元整數運算完成了計算量大的運算（矩陣乘法），因此我們的量化推理非常有效。而且，由於對錯誤敏感的累加器值是使用16位元整數儲存的，因此我們的解決方案非常準確，並且對量化誤差具有魯棒性。

　　在表1中，我們比較了在CPU，GPU和Google的Tensor處理單元（TPU）上解碼WMT’14英法開發集（newstest2012和newstest2013測試集的級聯，總共6003個句子）時的推理速度和品質。此處用於比較的模型僅在ML目標函數上使用量化約束進行訓練（即，不進行基於強化學習的模型優化）。在CPU和GPU上對模型進行解碼時，不會對其進行量化，並且所有操作均使用全精度浮點數完成。當在TPU上對其進行解碼時，某些操作（如詞嵌入查詢和注意力模組）仍保留在CPU上，所有其他量化操作均被裝載到TPU。在所有情況下，解碼都是在一臺具有兩個Intel Haswell CPU的計算機上完成的，該計算機總共包含88個CPU內核（超執行緒）。該機器配備了用於GPU實驗的NVIDIA GPU（Tesla k80）或用於TPU實驗的單個Google TPU。
　　表1顯示，在TPU上使用降低的精度演算法進行解碼時，對數困惑的損失非常小，僅爲0.0072，而BLEU則完全沒有損失。 該結果與以前的工作報告相符，即對折積神經網路模型進行量化可以保留大多數模型品質。
　　表1還顯示，在CPU上解碼我們的模型實際上比在GPU上快2.3倍。首先，我們的雙CPU主機在理論上提供了最高的FLOP效能，是GPU的三分之二。其次，集束搜尋演算法會迫使解碼器在每個解碼步驟中在主機和GPU之間進行大量的數據傳輸。因此，我們當前的解碼器實現無法充分利用GPU在理論上可以在推理過程中提供的計算能力。
　　最後，表1顯示，在TPU上的解碼比在CPU上的解碼快3.4倍，這表明TPU上的量化演算法比CPU或GPU都快得多。
　　除非另有說明，否則我們始終在實驗中訓練和評估量化模型。因爲從品質角度來看，在CPU上解碼的模型與在TPU上解碼的模型之間幾乎沒有區別，所以我們在訓練和實驗期間使用CPU進行解碼以進行模型評估，並使用TPU來服務產品。

7.解碼器

在給定已訓練模型的情況下，我們在解碼過程中使用集束搜尋來找到最高得分函數$s(Y,X)$對應的序列$Y$。我們對基於最大概率的集束搜尋演算法進行了兩個重要的改進：覆蓋罰分和長度歸一化。通過長度歸一化，我們旨在說明必須比較不同長度的假設這一事實。如果沒有某種形式的長度歸一化，則常規集束搜尋將平均傾向於較短的結果，而不是較長的結果，這是因爲在每個步驟中都新增了對數概率，從而爲較長的句子生成了較低（較負數）的分數。我們首先嚐試簡單地除以長度以進行歸一化。然後，我們通過除以$length^α$來改進原始啓發式演算法，其中$0<α<1$，其中α在開發集上得到了優化（通常發現$α∈[0.6-0.7]$是最佳的）。最終，我們在下面 下麪設計了經驗上更好的評分函數，該函數還包括覆蓋率懲罰，以便根據注意力模組支援完全覆蓋源語句的翻譯。
　　更具體地說，我們用來對候選翻譯進行排名的評分函數$s(Y,X)$定義如下：
$s(Y,X)=log(P(Y|X))/lp(Y)+cp(X;Y)$
$lp(Y)=\frac{(5+|Y|)^\alpha}{(5+1)^\alpha}\tag{14}$
$cp(X;Y)=\beta * \sum^{|X|}_{i=1}log(min(\sum^{|Y|}_{j=1}p_{i,j},1.0)),$
其中$p_{i,j}$是第$j$個目標詞$y_j$對第$i$個源詞$x_i$的注意力概率。通過構造（等式4），$\sum^{|X|}_{i=0}p_{i,j}$等於1。參數$α$和$β$控制長度歸一化和覆蓋損失的強度。當$α=0$和$β=0$時，我們的解碼器會按概率退回到純集束搜尋。
　　在集束搜尋期間，我們通常保留8-12個假設，但我們發現使用較少的假設（4或2）只會對BLEU分數產生輕微的負面影響。除了修剪一些假設的數目外，還使用了其他兩種修剪形式。首先，在每個步驟中，我們僅考慮具有區域性得分不超過該步驟的最佳字元的beamsize的字元。其次，在根據等式14找到歸一化的最佳分數之後，我們刪去所有比beamsize低於到目前爲止的最佳歸一化分數更大的假設。後者的修剪型別僅適用於完整假設，因爲它會比較歸一化空間中的分數，該空間僅在假設結束時纔可用。後一種修剪形式還具有以下作用：一旦找到足夠好的假設，就不會很快生成更多的假設，因此搜尋將很快結束。與未修剪相比，在CPU上執行時，修剪將搜尋速度提高了30％-40％（在這種情況下，我們會在預先確定的最大輸出長度爲源長度的兩倍後停止解碼）。通常，除非另有說明，否則我們使用$beamsize=3.0$。
　　爲了提高解碼期間的吞吐量，我們可以將許多類似長度的句子（通常最多35個）放入批次處理中，並對所有這些句子進行並行解碼，以利用針對並行計算優化的可用硬體。在這種情況下，只有在批次中所有句子的所有假設都超出集束的情況下，集束搜尋纔會結束，這在理論上效率較低，但實際上附加計算成本可忽略不計。