ResNet原理分析和程式碼實現

大數據實驗室 第N次 學習打卡

一、引入

ResNet是在2015年由微軟實驗室提出，作者是何愷明（本科清華、博士香港中文大學出來的大神）、孫劍（現任西安交大人工智慧學院首任院長）等人提出，其論文《Deep Residual Learning for Image Recognition》，斬獲當年ImageNet競賽中分類任務第一名，目標檢測第一名。（不說多了，就是NB）

二、提出ResNet的原因

折積網路發展史中，VGG最高達到了19層，再就是GoogleNet，達到了22層。
增加網路的寬度和深度可以很好的提高網路的效能，深的網路一般都比淺的網路效果好。比如說VGG，該網路就是在AlexNex的基礎上通過增加網路的深度大幅度提高了網路效能。但是，簡單地不斷增加深度，又會導致以下問題：

1. 梯度消失或者梯度爆炸
2. 模型過擬合
3. 計算資源的消耗
4. 退化問題
   問題1可以通過Batch Normalization可以避免。
   問題2可以通過增大數據量，配合Dropout來避免。
   問題3可以通過CPU叢集來解決。

但是問題4隨着網路層數的增加，網路發生了退化現象：隨着網路層數增加，訓練集錯誤率逐漸下降，然後趨於飽和，再增加深度時，錯誤率反而會增大，所以這並不是過擬合（過擬合在訓練中錯誤率應該是一直減小）。

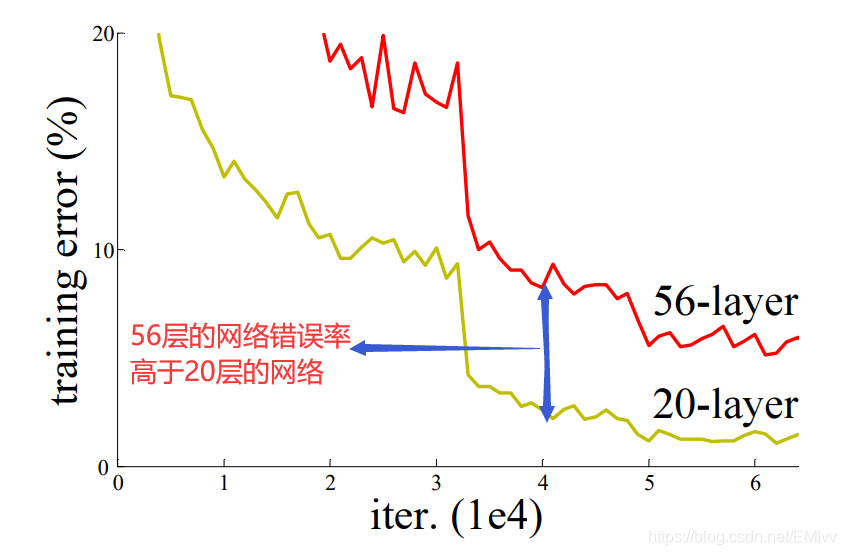
綜上，ResNet應運而生！

通過直接將輸入資訊繞道傳到輸出(shortcut / skip connection)，保護資訊的完整性，整個網路只需要學習輸入、輸出差別的那一部分，簡化學習目標和難度。VGGNet和ResNet的對比如下圖所示。

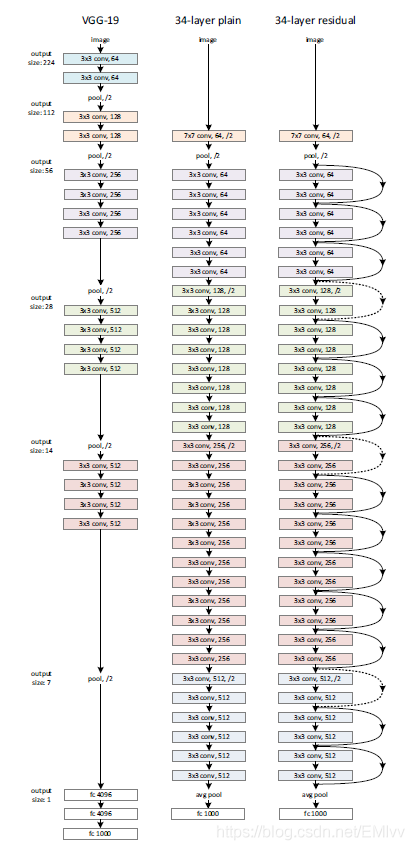
三、ResNet網路

1.網路結構

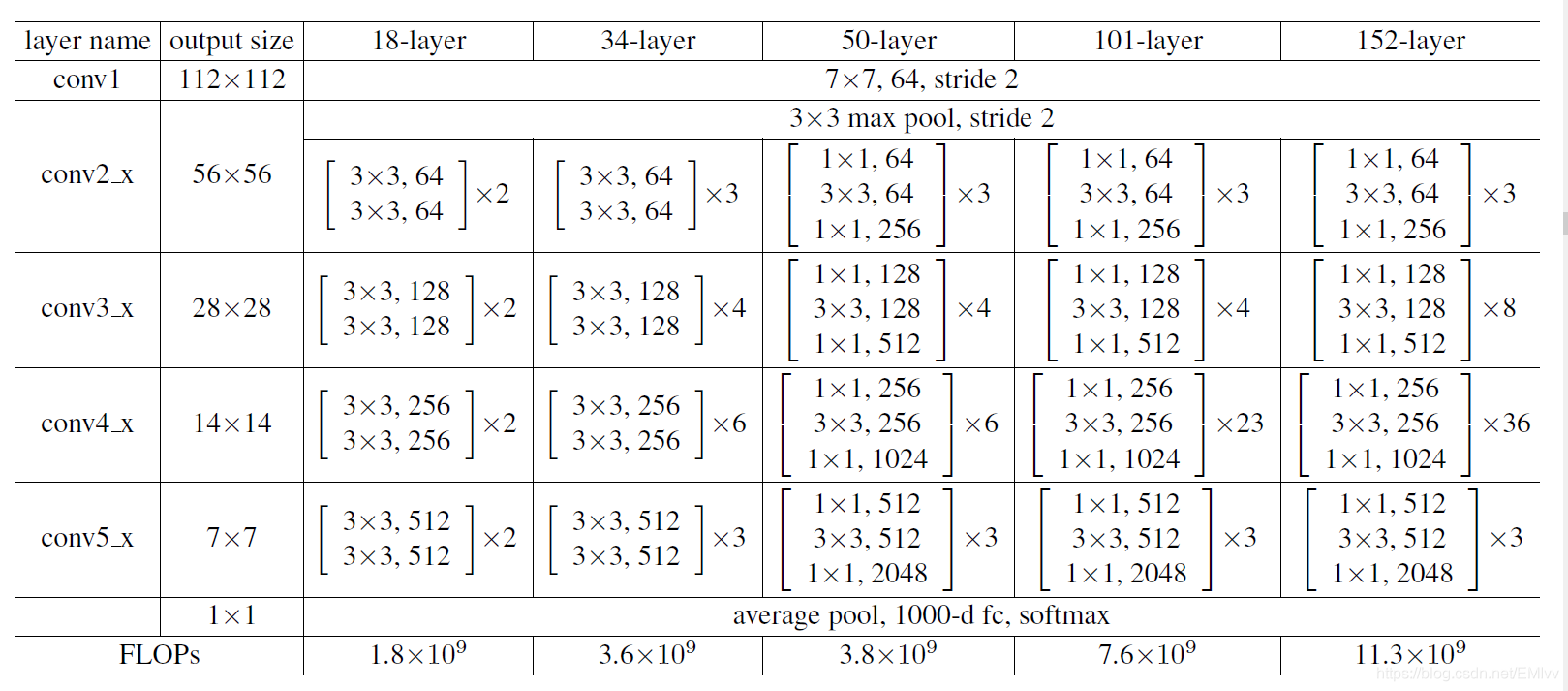
上表來自於原論文，展示了5種ResNet不同的結構，分別是18，34，50，101和152。

從第一列可以看出，所有的網路都由5部分組成：conv1_x, conv2_x, conv3_x, conv4_x, conv5_x。

以50層爲例:首先有個輸入7 x 7 x 64的折積層，然後經過3 + 4 + 6 +3 = 16個bulding block，每個block爲3層，所以由3 x 16 = 48層，最後有個fc層（全連線層），所以1 + 48 +1 = 50層。（我們一般說層數指的是折積層或者全連線層，不包括啓用層和池化層）

2.殘差函數

如果深層網路的後面那些層是恆等對映，那麼模型就退化爲一個淺層網路。那現在要解決的就是學習恆等對映函數了。 但是直接讓一些層去擬合一個潛在的恆等對映函數H(x) = x，比較困難，這就是深層網路難以訓練的原因。

但是，如果將這個問題轉換爲求解網路的殘差對映函數，也就是F(x)，其中F(x) = H(x)-x。

那麼咱們要求解的問題變成了H(x) = F(x)+x。

假設當前網路的深度能夠使得錯誤率最低，如果繼續增加咱們的層數（普通折積網路再增加就會出現網路退化問題了），爲了保證下一層的網路狀態仍然是最優狀態，咱們只需要把令F(x)=0就好了，因爲x是當前輸出的最優解，爲了讓它成爲下一層的最優解也就是希望咱們的輸出H(x)=x的話，是不是隻要讓F(x)=0就行了，只用小小的更新F(x)部分的權重值，不用像一般的折積層一樣大動幹戈。

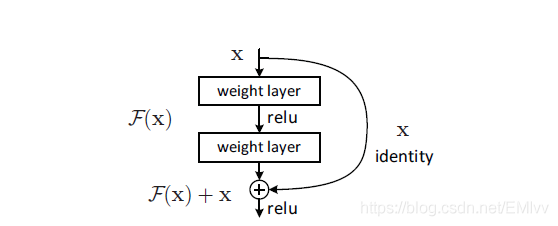
從ResNet網路結構圖中可以看出50層以下的和50層以上的ResNet有明顯差別，差別就在於殘差（residual）結構，50層以上採用BottleNeck(瓶頸，因爲非常像瓶頸)：

(有木有覺得我的圖畫得非常形象，hahahah)

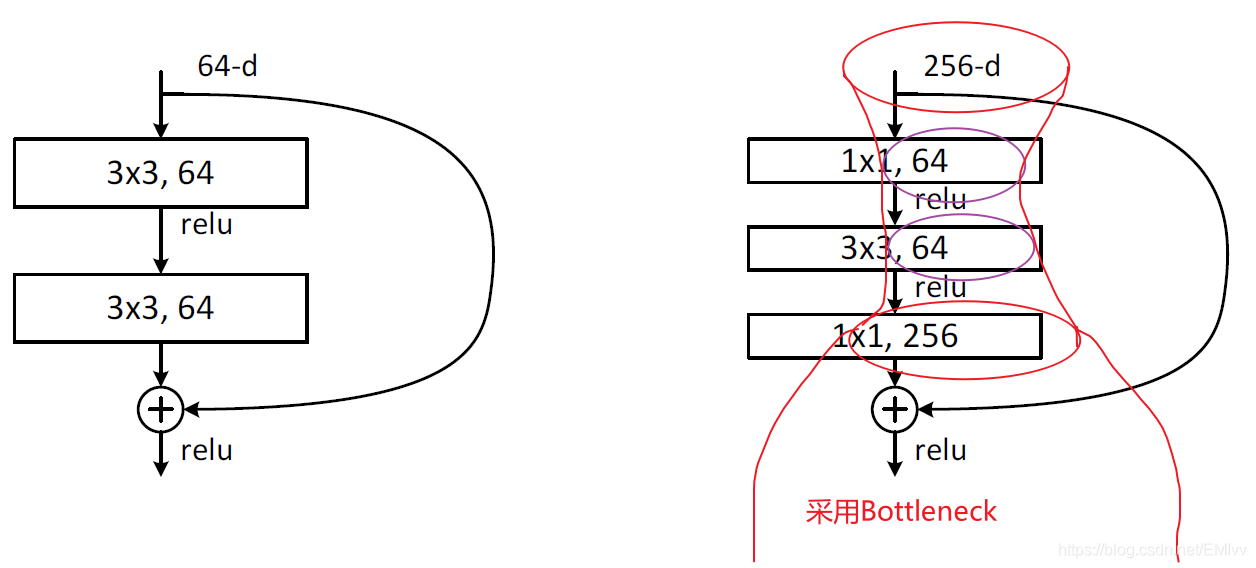
可以通過下面 下麪這個圖更加直觀的理解Bottleneck：

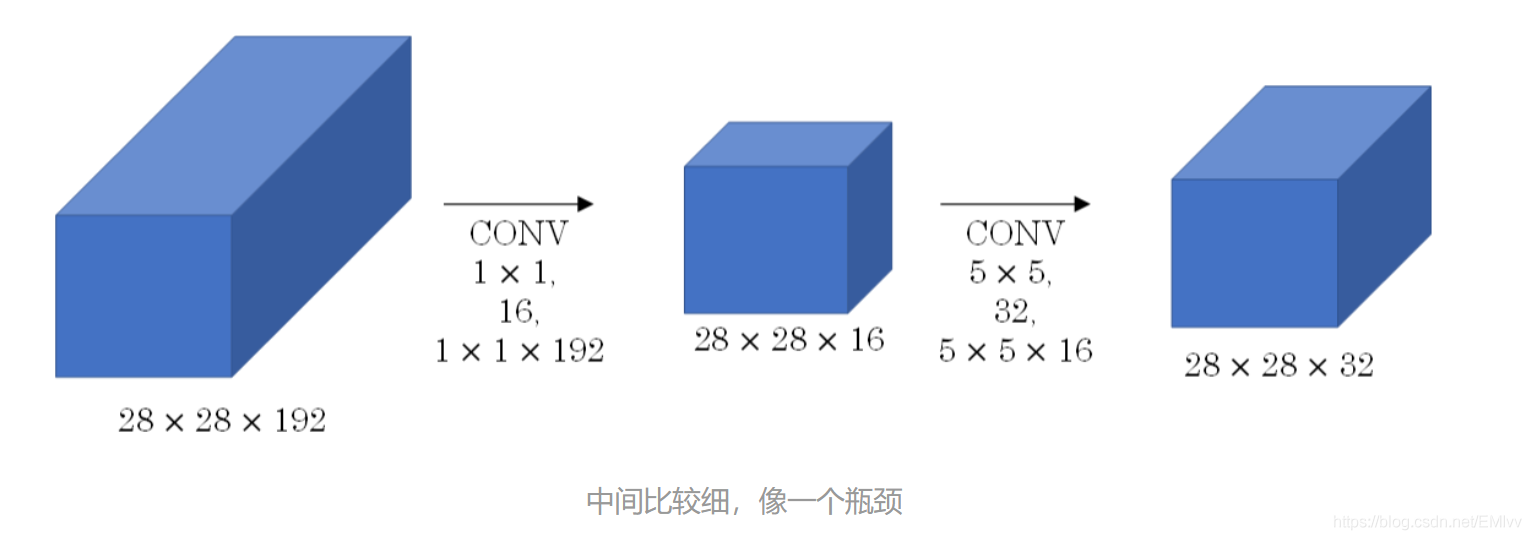
3.最大池化下採樣（Downsampling）

還是以34層的ResNet爲例：

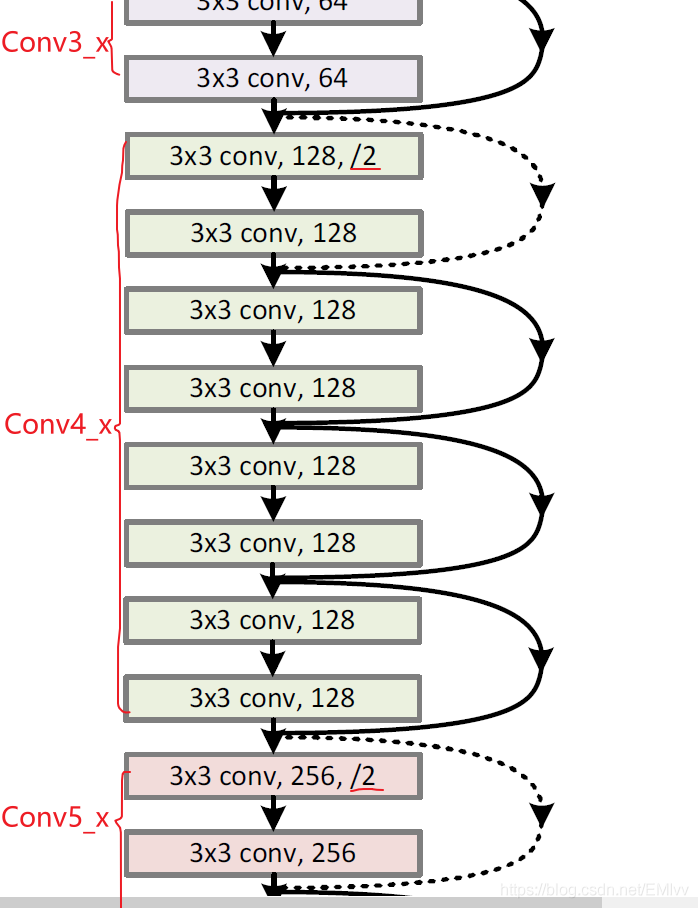
圖中的有向曲線稱爲shotcut（捷徑）或者skip connection，爲啥會有虛實之分呢？
之所以有虛線是因爲主分支（主分支的每一層都有預期的Size,如下圖）與shortcut的輸出特徵矩陣shape必須相同，所以需要通過最大池化下採樣對原輸入進行改變。

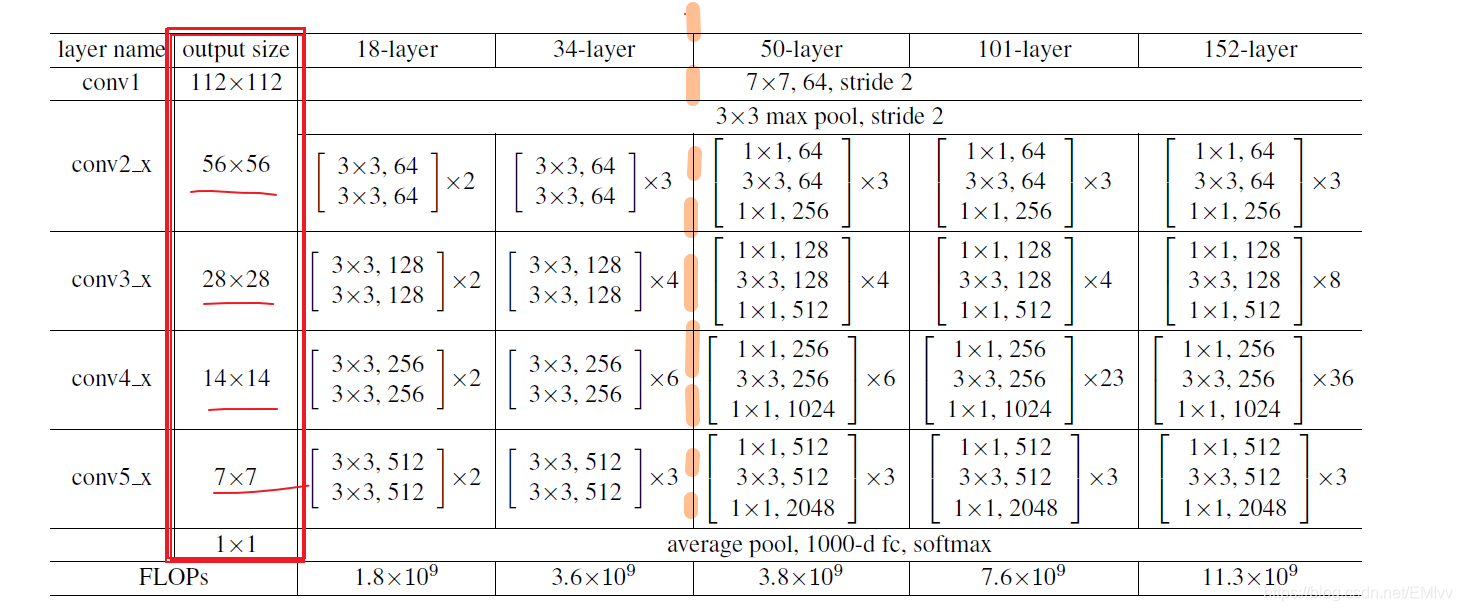
圖中我用黃色虛線分開了50層以下和50層以上的，是因爲它們的網路結構又有所不同，這裏的具體不同之處就是shortcut的虛實線：

• 50層以下只分別在Conv3、Conv4、Con5的第一個shortcut進行了最大池化下採樣，因爲Conv2的shortcut的輸入和主分支的輸出矩陣shape是一樣的。
• 50層及以上的相比前者，在Conv2的第一個shortcut就進行了最大池化下採樣，因爲主分支的輸出矩陣維度爲256，而shortcut的輸入矩陣維度爲64.

總之，一句話，就是必須保證主分支和shortcut的輸出矩陣的寬、高、維度必須一樣，因爲這樣才能 纔能對兩個矩陣進行相加！

四、基於keras實現ResNet-34程式碼

from keras.layers import Conv2D, BatchNormalization, Dense, Flatten,\
    MaxPooling2D, AveragePooling2D, ZeroPadding2D, Input, add
from keras.models import Model
from keras.utils import plot_model
from keras.metrics import top_k_categorical_accuracy

def conv_block(inputs, 
        neuron_num, 
        kernel_size,  
        use_bias, 
        padding= 'same',
        strides= (1, 1),
        with_conv_short_cut = False):
    conv1 = Conv2D(
        neuron_num,
        kernel_size = kernel_size,
        activation= 'relu',
        strides= strides,
        use_bias= use_bias,
        padding= padding
    )(inputs)
    conv1 = BatchNormalization(axis = 1)(conv1)

    conv2 = Conv2D(
        neuron_num,
        kernel_size= kernel_size,
        activation= 'relu',
        use_bias= use_bias,
        padding= padding)(conv1)
    conv2 = BatchNormalization(axis = 1)(conv2)

    if with_conv_short_cut:
        inputs = Conv2D(
            neuron_num, 
            kernel_size= kernel_size,
            strides= strides,
            use_bias= use_bias,
            padding= padding
            )(inputs)
        return add([inputs, conv2])

    else:
        return add([inputs, conv2])

inputs = Input(shape= [224, 224, 3])
x = ZeroPadding2D((3, 3))(inputs)

# Define the converlutional block 1
x = Conv2D(64, kernel_size= (7, 7), strides= (2, 2), padding= 'valid')(x)
x = BatchNormalization(axis= 1)(x)
x = MaxPooling2D(pool_size= (3, 3), strides= (2, 2), padding= 'same')(x)

# Define the converlutional block 2
x = conv_block(x, neuron_num= 64, kernel_size= (3, 3), use_bias= True)
x = conv_block(x, neuron_num= 64, kernel_size= (3, 3), use_bias= True)
x = conv_block(x, neuron_num= 64, kernel_size= (3, 3), use_bias= True)

# Define the converlutional block 3
x = conv_block(x, neuron_num= 128, kernel_size= (3, 3), use_bias= True, strides= (2, 2), with_conv_short_cut= True)
x = conv_block(x, neuron_num= 128, kernel_size= (3, 3), use_bias= True)
x = conv_block(x, neuron_num= 128, kernel_size= (3, 3), use_bias= True)

# Define the converlutional block 4
x = conv_block(x, neuron_num= 256, kernel_size= (3, 3), use_bias= True, strides= (2, 2), with_conv_short_cut= True)
x = conv_block(x, neuron_num= 256, kernel_size= (3, 3), use_bias= True)
x = conv_block(x, neuron_num= 256, kernel_size= (3, 3), use_bias= True)
x = conv_block(x, neuron_num= 256, kernel_size= (3, 3), use_bias= True)
x = conv_block(x, neuron_num= 256, kernel_size= (3, 3), use_bias= True)
x = conv_block(x, neuron_num= 256, kernel_size= (3, 3), use_bias= True)

# Define the converltional block 5
x = conv_block(x, neuron_num= 512, kernel_size= (3, 3), use_bias= True, strides= (2, 2), with_conv_short_cut= True)
x = conv_block(x, neuron_num= 512, kernel_size= (3, 3), use_bias= True)
x = conv_block(x, neuron_num= 512, kernel_size= (3, 3), use_bias= True)
x = AveragePooling2D(pool_size=(7, 7))(x)
x = Flatten()(x)
x = Dense(8, activation='softmax')(x)

model = Model(inputs= inputs, outputs= x)
# Print the detail of the model
model.summary()
# compile the model 
model.compile(optimizer='adam', 
        loss='categorical_crossentropy', 
        metrics=['acc',top_k_categorical_accuracy])
plot_model(model, to_file= 'C:/Users/12394/PycharmProjects/Keras/model_ResNet-34.png')

五、小結

在深度殘差網路的設計中通常都是一種「力求簡潔」的設計方式，只是單純加深網路，所有的折積層幾乎都採用3x3 的折積核，而且絕不在隱藏層中設計任何的全連線層，也不會在訓練的過程中考慮使用任何的 DropOut 機制 機製。

到目前爲止，在影象分類（ image classification ）、物件檢測（ object detection ）、語意分割（ semantic segmentation ）等領域的應用中，深度殘差網路都表現出了良好的效果。

參考資料

《Deep Residual Learning for Image Recognition》
程式碼參考：Keras大法（9）——實現ResNet-34模型