概念

教科書對stack / queue 一般都會同時進行介紹, 同時記憶比較好記.
stack 是後進先出. 後面進來的元素, 彈出的時候反而先走.
queue 是排隊(所以中文翻譯成佇列) , 先進先出. 可以想象成排隊買遊戲機的人, 喊到他了就高高興興交錢去了.

圖示

stack 可以用洗碗這個場景來記憶. 洗碗的時候, 我們都是一邊洗一邊把碗疊起來, 如下圖:

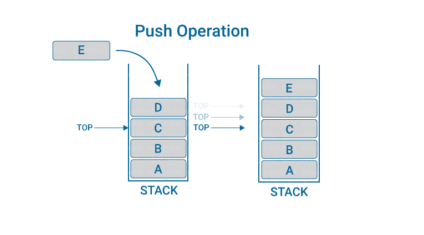
碗全部洗完之後, 要把它們挪到櫃子裡. 之前越是靠後的碗, 越是先被挪走, 如下圖:

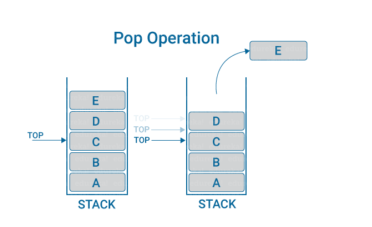
很好記.

主要操作

增加元素, 彈出元素, 似乎沒什麼特別可說的? 如果用C/Java 實現會涉及到"幽靈記憶體"問題. 不過現在程式設計一般都是直接使用語言本身內建的數據結構, 所以作爲一個不需要考試的中年人, 我就不用C/Java 來寫了, 偷懶用Python.

程式碼

class MyStack:

    """
    用python實現stack 會少了個很重要的概念: capacity resize , 因爲python本身的list 是動態陣列, 不需要處理擴容.
    """

    def __init__(self):
        self.data_list = []

    def get_size(self):
        return len(self.data_list)

    def push(self, data):
        self.data_list.append(data)

    def pop(self):
        if self.get_size() < 1:
            return None

        return self.data_list.pop()

    # 檢視當前物件(即最後一個), 但不刪除
    def peek(self):
        if self.get_size() < 1:
            return None

        return self.data_list[-1]

    def is_empty(self):
        return self.get_size() < 1

    def __repr__(self):
        return self.data_list.__str__()

python的list 其實已經實現了stack的功能, 所以這個程式碼真是偷懶到極致啊.

回答年輕時候的疑惑

在學校學習數據結構的時候, 我一直不太明白既然很多現代程式語言已經有了這些數據結構, 爲什麼我們要重寫一遍? 現在, 我穿越回去告訴自己:

從"以後專案是否會需要自己手寫這些最基礎的數據結構" 這個角度來看, 沒有必要. 重寫一遍的目的, 是讓大腦記下動手的經驗, 讓自己對相關知識的記憶更牢靠. 很多概念如果只是死記硬背不動手, 很快就會忘記.

另一個原因是, 在java/python這類語言裡都實現了動態列表, 記憶體的分配不用你管, 所以用來寫數據結構比較方便, 但不利於瞭解指針和記憶體泄露這些概念. 如果想讓基礎更紮實,那麼最好重寫一遍.

<演算法4> 這本書裡有java實現的stack, 也提到了幽靈記憶體的概念, 所以java版本就不寫了. 在最後寫完python會再寫個C版本練練手.

應用-計算表達式

在很多實際應用中, 用stack 處理會達到很巧妙的類似魔法的效果. 這裏舉3個應用的例子: 實現計算表達式, 迷宮闖關和遍歷樹. 遍歷樹會在後面再寫, 這裏就寫計算表達式.

這個例子是從<演算法4> 這本書看來的, 當時拍案叫絕啊. 結果自己用python默寫出來又翻車了.

需求

寫一個程式, 能夠計算以下3個字串表達式的結果:

1. 15 + 21
2. 8 * ( 11 - ( 7 + ( 3 + 5 ) ) )

有問題的程式碼

#! /usr/bin/python
# -*- coding: UTF-8 -*-

"""

    作者: 小肥巴巴
    簡書: https://www.jianshu.com/u/db796a501972
    郵箱: [email protected]
    github: https://github.com/xiaofeipapa/algo_example

    您可以任意轉載, 懇請保留我作爲原作者, 謝謝.

"""
from stack_v_1 import MyStack


def cal_each(before, last, opt):
    before = float(before)
    last = float(last)

    if opt == '+':
        return before + last
    elif opt == '-':
        return before - last
    elif opt == '*':
        return before * last
    elif opt == '/':
        return before / last

    else:
        raise Exception('不支援的操作: ', opt)


def calculator(input_str):
    """
    計算 數值表達式
    :param input_str:
    :return:
    """

    opt_list = ['+', '-', '*', '/']

    opt_box = MyStack()  # 存放操作符
    val_box = MyStack()  # 存放值

    step = 0
    for i in range(0, len(input_str)):
        val = input_str[i].strip()
        if not val:
            continue

        """
            運算規則, 當val 是 ) 時, 捨棄進入下一個回圈
            當val 是 ) 開始計算
            當val 是操作符或者值時, 進入各自的stack
            更詳細見圖形分析
        """

        if val == '(':
            pass

        elif val in opt_list:
            opt_box.push(val)
        elif val == ')':

            # 開始計算, 彈出最近的操作符, 最近的兩個數
            opt = opt_box.pop()

            """
            1) 彈出的先後順序很重要, 應該後入的在後(減法和除法都是從左到右)
            2) 不能用 python的eval, 否則就沒達到鍛鍊目的
            """
            last = val_box.pop()
            before = val_box.pop()

            result = cal_each(before, last, opt)
            if val_box.is_empty():
                print('--- 計算結果: ', result)
                return result

            # 否則推到stack 裡準備下一個運算
            val_box.push(result)

        else:
            # 正常的值, 推入
            val_box.push(val)

        step += 1
        print('--- 第 %d 步: ' % step)
        print('--- val_box: ', val_box)
        print('--- opt_box: ', opt_box)
        print('\n\n')

    # -------- end for
    raise Exception('不可能到這裏, 程式設計有問題')


def test_it():

    str_1 = '8 * ( 11 - ( 7 + ( 3 + 5 ) ) )'
    calculator(str_1)

    # 意外"驚喜": 這個程式不識別11, 如何識別多位數?
    # 需要先對錶達式進行一次掃描.


if __name__ == '__main__':
    test_it()

程式碼解說

在python裡, 其實直接 eval 就可以計算, 不過既然是練習當然要自己動手. 而且練熟了這種思路會對以後工作很有幫助. 舉個例子, 某個生產廠希望你能寫一個簡單的規則程式, 實現有限的操作指令的組合, 達到"智慧"的效果. 這類規則程式的演算法一般就是計算器的演算法改動版.

在這個演算法實現裡, 原書作者巧妙地用兩個stack 分別儲存操作符和計算值. 我在程式碼裡加了print, 可以一步步看到兩個stack 是怎麼一步步儲存數據的:

# 待計算的表達式:  8 * ( 11 - ( 7 + ( 3 + 5 ) ) )

--- 第 1 步: 
--- val_box:  ['8']
--- opt_box:  []



--- 第 2 步: 
--- val_box:  ['8']
--- opt_box:  ['*']



--- 第 3 步: 
--- val_box:  ['8']
--- opt_box:  ['*']



--- 第 4 步: 
--- val_box:  ['8', '1']
--- opt_box:  ['*']

在值的檢查判斷裡, 左括號"(" 是被省略的, 右括號纔是真正計算的開始:

elif val == ')':

            # 開始計算, 彈出最近的操作符, 最近的兩個數
            opt = opt_box.pop()

            """
            1) 彈出的先後順序很重要, 應該後入的在後(減法和除法都是從左到右)
            2) 不能用 python的eval, 否則就沒達到鍛鍊目的
            """
            last = val_box.pop()
            before = val_box.pop()

            result = cal_each(before, last, opt)
            if val_box.is_empty():
                print('--- 計算結果: ', result)
                return result

            # 否則推到stack 裡準備下一個運算
            val_box.push(result)

當遇到右括號的時候, 從值stack 連續彈兩個數出來進行, 操作符opt_stack裡彈一個操作符, 三者進行操作. 由於stack 是後進先出的特性, 所以這個計算必然是最內層(靠右)的計算. 操作完之後, 壓回到stack, 下次再彈出的必然也是它, 符合需求.

翻車在哪

思路沒有問題, 那麼這段程式翻車在哪? 主要在兩個地方:

1. 原書裡, 所有表達式的輸入用命令列進行, 所以可以確保每一次輸入都是完整的數位. 當我把輸入放在字串的時候, 數位 11 被回圈拆分爲兩個1進行計算, 導致了bug.
2. 在彈出值進行操作的時候只考慮到二元操作符, 所以每次都彈兩個值. 類似 sqrt 這種一元操作符, 其實只需要一個值.

解決辦法: 第二個問題好解決, 麻煩的是第一個. 但是我想了想還是解決吧, 太多演算法的範例像是玩具, 還不如在複習演算法的時候就寫點實用程式碼.

修改版

修改版如下:

#! /usr/bin/python
# -*- coding: UTF-8 -*-

"""

    作者: 小肥巴巴
    簡書: https://www.jianshu.com/u/db796a501972
    郵箱: [email protected]
    github: https://github.com/xiaofeipapa/algo_example

    您可以任意轉載, 懇請保留我作爲原作者, 謝謝.

"""
from my_statck import MyStack
import math


def handle_temp_value(opt_box, temp_opt, val_box, temp_value):

    # 處理數值
    if len(temp_value) > 0:
        val_box.push(''.join(temp_value))
        temp_value.clear()

    # 處理操作符
    if len(temp_opt):
        opt_box.push(''.join(temp_opt))
        temp_opt.clear()


def cal_each(opt_box, val_box):

    """
    1) 彈出的先後順序很重要, 應該後入的在後(減法和除法都是從左到右)
    2) 不能用 python的eval, 否則就沒達到鍛鍊目的
    """

    opt = opt_box.pop()

    if opt not in ['+', '-', '*', '/', 'sqrt']:
        raise Exception('不支援的操作: ', opt)

    # 彈出最近的數
    last = float(val_box.pop())

    if opt == 'sqrt':
        result = math.sqrt(last)

    else:

        # 彈出前一個數
        before = float(val_box.pop())

        if opt == '+':
            result = before + last
        elif opt == '-':
            result = before - last
        elif opt == '*':
            result = before * last
        else:
            result = before / last

    val_box.push(result)
    return result


def calculator(input_str):
    """
    計算 數值表達式
    :param input_str:
    :return:
    """

    opt_list = ['+', '-', '*', '/']

    opt_box = MyStack()         # 存放操作符
    val_box = MyStack()         # 存放值

    # 增加兩個容器來處理多位數和操作符
    temp_value = list()         # 臨時容器, 儲存多位數
    temp_opt = list()           # 臨時容器, 儲存字串

    step = 0
    for i in range(0, len(input_str)):
        val = input_str[i].strip()
        if not val:
            continue

        """
            運算規則, 當val 是 ) 時, 捨棄進入下一個回圈
            當val 是 ) 開始計算
            當val 是操作符或者值時, 進入各自的stack
            更詳細見圖形分析
        """

        # 先處理數值. 數值有可能是小數
        if val == '.' or val.isdigit():
            temp_value.append(val)

        elif val.isalpha():
            temp_opt.append(val)

        else:

            # 處理臨時數據
            handle_temp_value(opt_box, temp_opt, val_box, temp_value)

            if val == '(':
                pass

            elif val in opt_list:
                opt_box.push(val)

            elif val == ')':

                result = cal_each(opt_box, val_box)

        step += 1
        # print('--- 第 %d 步: ' % step)
        # print('--- val_box: ', val_box)
        # print('--- opt_box: ', opt_box)
        # print('\n\n')

    # -------- end for
    # 處理臨時數據
    handle_temp_value(opt_box, temp_opt, val_box, temp_value)

    if opt_box.is_empty():
        result = val_box.pop()
    else:

        while not opt_box.is_empty():
            result = cal_each(opt_box, val_box)

    print('==== 最終計算結果: %0.4f' % result)


def test_it():

    str_1 = '8 * ( 11 - ( 7 + ( 3 + 5 ) ) )'
    calculator(str_1)

    str_1 = ' 15 + sqrt(9) - (20 + 2 )'
    calculator(str_1)

    str_1 = ' 15 + 21'
    calculator(str_1)


if __name__ == '__main__':
    test_it()

修改版多考慮了兩個場景:

1. 計算值可能是多位數據, 所以要加一個臨時容器進行處理.
2. 操作符也有可能是單詞而不是加減乘除單個字元, 所以也要加個容器處理.

這樣設計的好處是一邊掃描字串一邊進行計算, 效率高, 不好的地方是難以擴充套件: 如果使用者的輸入不規範怎麼辦? 怎麼先進行處理? 是不是又要在主程式裡加一堆變數?

所以更好的做法是將主程式拆分成兩部分: 一部分進行數據清洗, 確認數據沒有問題. 另一部分進行邏輯計算. 不過這已經涉及到具體業務, 而不是複習演算法了, 就有待各位自己把玩了.

寫首歪詩來記住

程式設計師的特點是一週之後會忘記自己的程式碼. 一大段程式就像一大段文章, 原封不動記下來是不可能的, 所以要提煉並記憶一些要點, 根據這些優點複寫其他部分. (想想大廠面試要手寫演算法, 還是有點道理的)

於是乎, 獻上歪詩一首:

清洗識別多位數,    # 清洗數據, 識別一元操作符和單詞操作符
兩個容器放在前.    # 用兩個stack 分別記錄操作符和值
右括號纔是計算.    # 遇到)纔開始計算
彈值順序有先後 先後.    # 某些操作符有順序要求, 先談哪個值很重要

搞定!