前言

自己在課上吹的牛，課程作業再麻煩也得幹。模了好幾天魚，終於在DDL前一天弄完了慣導模組的簡單demo，卡爾曼濾波算是我弄的最久的了（大概2-3天），雖然沒有徹底弄懂原理（概率論沒學，隱馬爾可夫鏈啥的更是不會），好歹就着教學推導給實現了。
實現的效果不咋的，還是存在明顯的跳動，估計是MPU6050陀螺儀的事，方差大、數值基本是不準不準的，爬了。

理論推導

假定條件

使用陀螺儀和加速度計實現卡爾曼濾波有幾個基本假設，我碼字的時候忘了幾個，先列出來，以後想起來再填。

線性系統。對於穩態卡爾曼濾波，應該是線性時不變系統？
靜態條件，也就是隻有重力加速度G的情況下，才能纔能使用加速度推導出歐拉角。

歐拉角和四元數

這個部分其實只用瞭解一下歐拉角即可，但是作爲一個開發備忘，繞任意軸旋轉的矩陣、四元數還是要有的，萬一以後用到了呢（狗頭）。

歐拉角

我們這裏說的歐拉角是Z-Y-X歐拉角，也就是先繞Z軸旋轉α角，再繞Y軸旋轉β角，最後繞X軸旋轉γ角。示意圖大概是這麼個樣子。一般Z軸取鉛垂軸，X軸爲物體主對稱軸，Y軸爲輔對稱軸或用右手定則確定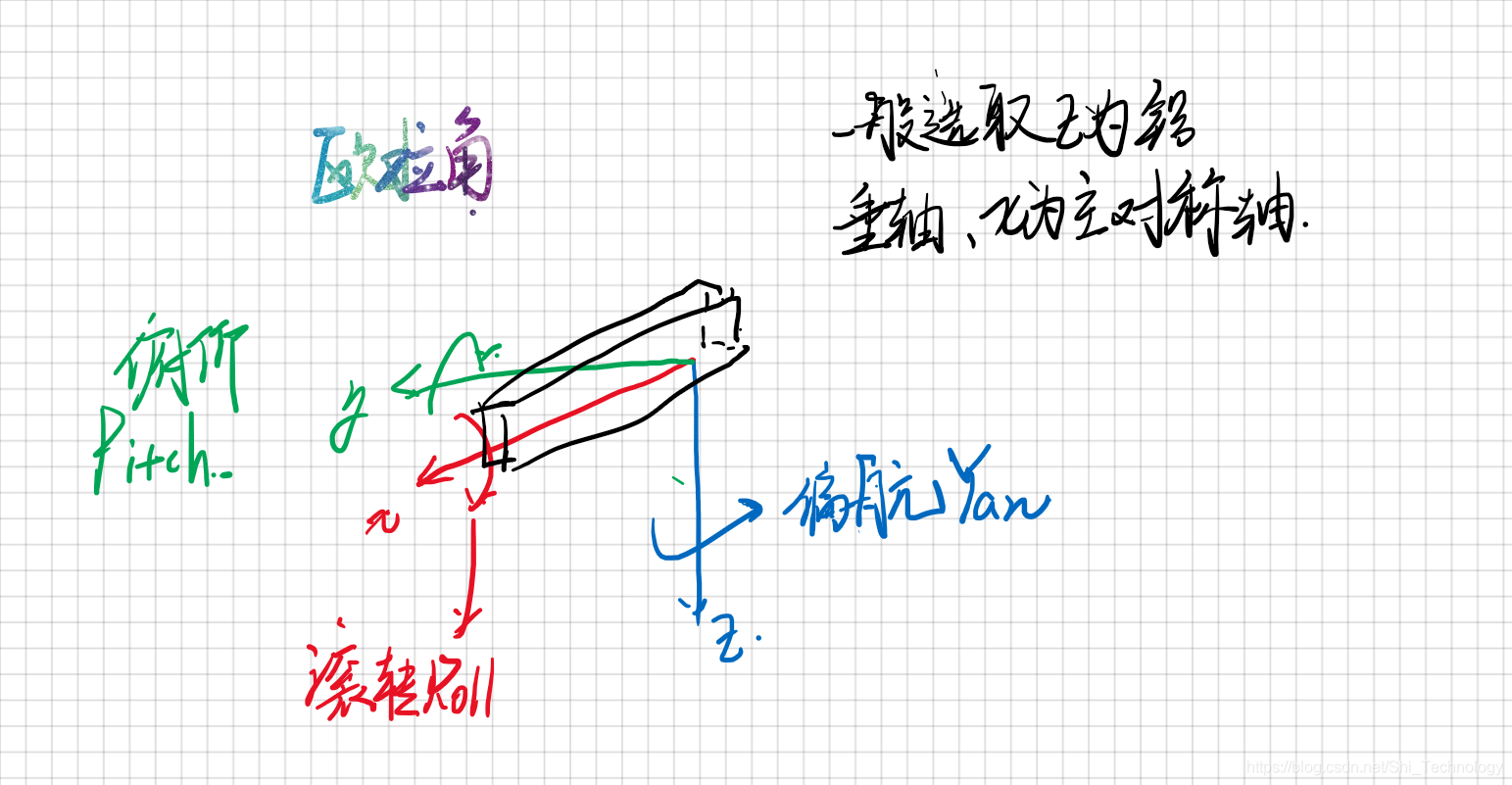欧拉角示意图
那麼我們就將繞Z軸旋轉的角度Yaw稱爲偏航，繞X軸旋轉的角度稱爲Roll滾轉，繞Y軸旋轉的角度Pitch稱爲俯仰角。

繞任意軸旋轉的矩陣（Goldman公式）

歐拉角實際上是一種轉角排列設定法，轉角的排列順序比較多，但是很多旋轉實際上是一樣的。我們可以找到一個等效的旋轉軸和對應這個軸的轉角，那麼我們假定 $\hat{K}是一個表示旋轉軸的單位向量，R_{K}(θ)爲等效旋轉矩陣$
那麼我們可以將被旋轉向量V分解爲沿軸分量V_c和V_1，利用向量叉積取垂直V_c和V_1的V_2。設旋轉後的向量爲V’,其在平面分量爲V’_1，有： $\vec{V} = \vec{V_{c}}+\vec{V_{1}}$
$\vec{V^{'}} =\vec{V_{c}}+\vec{V_{1}^{'}}$
示意圖（意思意思就行了（狗頭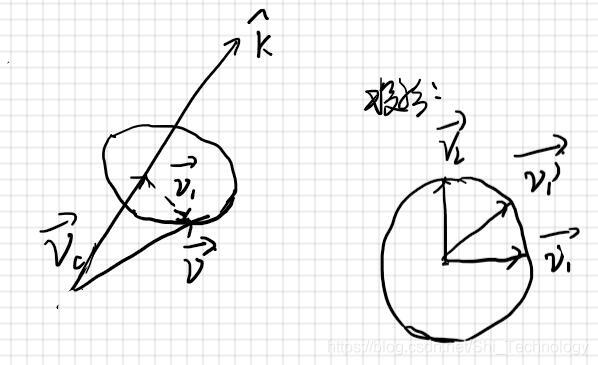））在这里插入图片描述
下面下麪就是用V_1和V_2表示旋轉後的向量投影，假設轉角爲θ，θ實際上就是V’_1和V_1的夾角（圖上忘畫了），那麼旋轉後的向量就是：
$\vec{V^{’}}=\vec{V_{c}}+\vec{V_{1}}cosθ+\vec{V_{2}}sinθ$
帶入軸K的單位向量表示和各個座標軸的座標即可得到Goldman公式。例如：
$\hat{K} = (K_{x},K_{y},K_{z}),\vec{V_{c}}= (\vec{V_{c}}\cdot\hat{K})\hat{K}$
如果令V=（1，0，0），即X軸，那麼代入旋轉後向量公式就可以求得矩陣的第一列。
最後的旋轉矩陣應該是：
$\left[ \begin{matrix} K_{x}^{2}(1-c)+c & K_{x}K_{y}(1-c)-K_{z}s & K_{x}K_{z}(1-c)-K_{y}s \\ K_{x}K_{y}(1-c)+K_{z}s & K_{y}^{2}(1-c)+c & K_{y}K_{z}(1-c)-K_{x}s \\ K_{x}K_{z}(1-c)-K_{y}s & K_{z}K_{y}(1-c)+K_{x}s & K_{z}^{2}(1-c)+c \end{matrix} \right]$
其中c爲cosθ，s爲sinθ。

四元數/歐拉參數

基於上面的繞任意軸旋轉的公式，我們可以使用4個數值表示旋轉，這四個數值稱爲歐拉參數，可以視爲一個單位四元數：
$\varepsilon_{1} = k_{x}sin\frac{\theta}{2}$
$\varepsilon_{2} = k_{y}sin\frac{\theta}{2}$
$\varepsilon_{3} = k_{z}sin\frac{\theta}{2}$
$\varepsilon_{4} = cos\frac{\theta}{2}$
這四個參數滿足：
$\varepsilon_{1}^{2}+\varepsilon_{2}^{2}+\varepsilon_{3}^{2}+\varepsilon_{4}^{2} =1$

推導

說是推導，實際上就是說明幾個符號的意義和演算法的邏輯，真要看推導還得看參考文獻1和3。
在這裏，我們使用大寫字母（比如X）表示矩陣，使用小寫+斜體表示一個列向量,例如： $\boldsymbol{\hat{x}_{k-1|k-1}}和\boldsymbol{\hat{x}_{k|k-1}}$
注意上面兩個例子的下標和上標，\hat表示該值/向量爲預測得到的，而k-1|k-1表示k-1時刻該值/向量爲經過k-1時刻卡爾曼濾波計算後得到，k|k-1則表明這是利用k-1時刻對k時刻進行的預測（沒有經過卡爾曼濾波）。

首先建立系統的狀態空間方程（應該是這麼說？）
$\boldsymbol{{x}_{k}} = F\boldsymbol{{x}_{k-1}+B\boldsymbol{{u}_{k}}+\boldsymbol{{w}_{k}}} ——(1)$
$\boldsymbol{{z}_{k}} = H\boldsymbol{{x}_{k}}+\boldsymbol{{v}_{k}} ——(2)$
式中： $\boldsymbol{{x}_{k}}爲k時刻系統的狀態向量（同時也是你需要的濾波結果向量）$
$\boldsymbol{{u}_{k}}爲k時刻系統的輸入向量（也就是輸入的控制量）,而\boldsymbol{{z}_{k}}爲觀測$
$向量(一般與\boldsymbol{x}不同);\boldsymbol{{w}_{k}}爲過程噪聲,\boldsymbol{{w}_{k}}\sim N(0,\boldsymbol{Q_{k}}),\boldsymbol{Q_{k}}爲過程噪$
$聲協方差矩陣；\boldsymbol{{v}_{k}}爲觀測噪聲,\boldsymbol{{v}_{k}}\sim N(0,\boldsymbol{R_{k}}),\boldsymbol{R_{k}}爲觀測噪聲協$
$方差矩陣；F表示k-1時刻對k時刻的影響，B表示輸入對狀態的$
$影響;H將狀態向量對映到觀測向量空間，是一個線性對映。$
基於（1）（2）式，我就開始推導(列公式)了。首先是預測過程，如果不考慮噪聲，我們的預測是：
$\boldsymbol{\hat{{x}}_{k|k-1}}= F\boldsymbol{\hat{{x}}_{k-1|k-1}+B\boldsymbol{{u}_{k}}} ——(3)$
然後是對於協方差矩陣P進行預測，協方差矩陣P的定義是：
$\boldsymbol{P_{k}}= Cov(\boldsymbol{\boldsymbol{{x}_{k}}-\hat{{x}}_{k|k-1},\boldsymbol{\boldsymbol{{x}_{k}}-\hat{{x}}_{k|k-1}})}$
對(1)和(3)做差，然後由於Q和預測無關，我們就可以得到對P的預測值:
$\boldsymbol{{P}_{k|k-1}}= F\boldsymbol{{P}_{k-1|k-1}}F^{T}+Q ——(4)$

對於MPU6050，我們設定觀測變數爲：
$\boldsymbol{{x}_{k}} = \left[\begin{matrix} \theta \\ \dot{\theta}_{bias} \end{matrix}\right]， \dot{\theta}_{bias}爲角速度偏差值$
顯然，這兩個是不相乾的，因此協方差矩陣Q爲一個對角陣，輸入變數U爲：
$\boldsymbol{{u}_{k}} = \dot{\theta} ， \dot{\theta}爲角速度$
那麼矩陣F、B、Q爲,dt爲採樣時間，Q_{θ}爲角度的協方差：
$\boldsymbol{F} = \left[\begin{matrix} 1 &dt \\ 0 & 1 \end{matrix}\right];\boldsymbol{B} = \left[\begin{matrix} dt \\ 0 \end{matrix}\right];\boldsymbol{Q} = \left[\begin{matrix} Q_{\theta} &0 \\ 0 & Q_{\dot\theta_{b}} \end{matrix}\right]\cdot dt$
關於協方差矩陣P，其初始化值其實不需要非常關心。因爲如果是線性時不變系統，在經過一段時間後P會迭代到一個穩態的值，初值只是會改變這個迭代的速度。如果初始值是精確的，那麼完全可以初始爲一個0陣；對於我們這樣設定的狀態變數，因爲其相互獨立，所以P也是個對角陣，P可以初始化爲,爲一個比較大的值：
$\boldsymbol{P}= \left[\begin{matrix} L &0 \\ 0 & L \end{matrix}\right]$
下面下麪是觀測：
根據（2）式，我們先來討論一下向量和矩陣。
爲了便於在C語言中實現，我們這裏用的是二維的單獨解算，如果我們設定觀測向量爲單純某個角度（比如滾轉角Roll），那麼就不需要求矩陣的逆（具體原因後面說），大大簡化運算。
因此，觀測向量爲一個角度標量，這個角度通過加速度算出；同樣，觀測噪聲矩陣R也爲一個標量。
$\boldsymbol{z_{k}} = f(\boldsymbol{Accx_{k}},\boldsymbol{Accy_{k}},\boldsymbol{Accz_{k}});\boldsymbol{H}=\left[\begin{matrix} 1 &0 \end{matrix}\right]$
關於R的值，R越大，證明我們對觀測結果越不信任，會使得響應變慢；如果過小，那麼噪聲影響就會比較大。
觀測我們先需要通過加速度獲取觀測值，這裏用參考博文2 的atan2那個方法進行計算，具體可以看那篇博文。
然後計算預計和觀測的誤差,顯然這個誤差是個標量(scalar)：
$\boldsymbol{y_{k}} =\boldsymbol{z_{k}} -H\boldsymbol{\hat{x}_{k|k-1}}$
然後爲了方便計算，我們將一箇中間變數定義爲矩陣S，在參考博文1中作者稱其爲innovation covariance，我也不知道是啥。
$S = HP_{k|k-1}H^{T}+R$
在我們這個情況下，這個矩陣S是一個標量，因此後面對其求逆時只需要做除法（填坑）。
下面下麪進行演算法的下一步：計算卡爾曼增益：
$K_{k} = P_{k|k-1}H_{T}S^{-1}——(5)$
$對於我們具體實現，可以寫爲：K_{k} = \frac{P_{k|k-1}H^{T}} {[S]}$
有了這一步的卡爾曼增益，我們就可以對預測和觀測進行Fusion了：
$\boldsymbol{\hat{x}_{k|k}} =\boldsymbol{\hat{x}_{k|k-1}} +K_{k}\boldsymbol{\hat{y}_{k}} ——(6)$
最後一步就是實現協方差矩陣P的更新：
$\boldsymbol{P_{k|k}} =(I-K_{k}H)\boldsymbol{P_{k|k-1}} ——(7)$

卡爾曼濾波調參：

調參這個問題，我不是很明白，只能大概說一下，可能沒啥用，反正這篇博文是爲以後開發做備忘。
參數有：協方差矩陣P的初始值，狀態向量x的初始值，過程噪聲矩陣Q，測量噪聲矩陣R
對於狀態向量x的初始值，其實也不是一個參數，因爲初始情況一般已知。如果說具體實現，那就保持靜止採幾百個樣，求均值基本就行。
對於P的初值，其實沒太有影響，P的初始值只是影響卡爾曼濾波的收斂速度，如果對初始觀測十分確定，取0陣就行。
比較難確定的就是過程噪聲矩陣Q和測量噪聲矩陣R，這裏的參數我是抄第一篇博文的，具體怎樣通過實驗測定我也不是很清楚。

卡爾曼濾波實質：

對於一維的情況來說，卡爾曼濾波實際上是兩個正太分佈的乘積\疊加，我們通過kalman得到的估計值實際上就是這個疊加的新期望值，具體的可以看參考文章3.

C實現

這個網上很多，博主趕着打遊戲，有空再填（狗頭）。

Python實現

import numpy as np
import matplotlib.pyplot as plt
import math
#compute the sigma of accel and gryo's measurement
dataset =  np.loadtxt(r'C:\Users\Lin\Desktop\ProjectFisher\navigation\ckalman.csv',delimiter=',')
sigma = np.std(dataset,axis = 0)
print(sigma)
print(dataset.mean(axis = 0))
gryo_x = dataset[:,0]
accel_z = dataset[:,5]
accel_y = dataset[:,4]
accel_x = dataset[:,3]
RollC = dataset[:,6]
K1C = dataset[:,7]
K2C = dataset[:,8]
n = accel_x.shape[0]
#kalman compute 
'''
對於MPU6050進行卡爾曼濾波的前提條件：
1. 線性時不變系統
2. 鉛墜方向加速度爲一定值，如果不是，那麼應該用磁強計進行角度觀測
3. 以後再補充
'''
TimeList = [i/2 for i in range(0,n,1)]#時間序列
GAngle = 0
GAngleList = []#預測得到的角度
AAngleList = []#觀測值得到的角度
KAngleList = []#Kalman濾波後的角度
KalmanList = []#Kalman 增益值1
KalmanList2 = []#Kalman 增益值2
BiasList = []
angle = 0#初始角度爲0
bias = 0 #初始的角速度偏差爲0

#參量：dt採樣時間，P初始協方差矩陣（與收斂有關），Q過程噪聲矩陣（越大預測可信度越低），測量噪聲矩陣R（R越大觀測可信度越低）
dt = 0.5
X = np.array([[angle],[bias]]) #預測變數
Gryo = 0 #輸入控制變量
Z = 0 #觀測量，爲加速度計算出的角度.實際上，加速度計算出的角度，只能說鉛錘軸的加速度g不變推導出的
Y =0#觀測量與預計值的誤差，Y = Z-HX
P = np.array([[1,0],[0,1]]) #初始化協方差矩陣P,P是一個對角陣，[L,0;0,L]L是一個很大的數；如果已知初始狀態，那麼認爲置信度100%，即爲0陣
Q = np.array([[0.001,0],[0,0.17]])#過程噪聲矩陣，角度的協方差來自TKJ，角速度爲測量得到的方差，實際上真正的過程噪聲矩陣還應該xdt
R = 0.01 #測量噪聲矩陣，由於是二維且只有角度，因此轉換爲標量，使用加速度的方差

F = np.array([[1,-dt],[0,1]])
B = np.array([[dt],[0]])#輸入作用於預測的矩陣B
H= np.array([[1,0],])#狀態轉移矩陣，將預測空間的變數對映到觀測空間，這裏的觀測是角度（使用加速度分量計算而得出）
K = np.array([[0],[0]])#卡爾曼增益
I =np.array([[1,0],[0,1]])#單位矩陣

for i in range(0,n,1):
    Gryo = gryo_x[i]

    #計算預測得到的結果
    GAngle += Gryo*dt
    GAngleList.append(GAngle)
    
    X =np.dot(F,X)+np.dot(B,Gryo) # 根據k-1時刻計算k時刻預測值
    P = np.dot(np.dot(F,P),F.T)+Q*dt #根據k-1時刻估計的協方差矩陣
    Roll = math.degrees(math.atan2(accel_y[i],accel_z[i]))
    #Roll角還可以通過atan(accY/sqrt(accX^2+accZ^2))計算,網上的歐拉角計算有兩種方式，
    #參考https://blog.csdn.net/qcopter/article/details/51848544
    Z = Roll
    AAngleList.append(Z)#計算單純觀測得到的結果
    Y =Z - np.dot(H,X)
    S = np.dot(np.dot(H,P),H.T)+R #中間變數，S理論上應該是矩陣，在最後計算卡爾曼增益時需要取inv（S），但是這裏S是scalar，因此求逆只需要做除法
    K = np.dot(P,H.T)/S#計算卡爾曼增益
    X = X+K*Y #卡爾曼濾波後的預測值
    P = np.dot(I-np.dot(K,H),P)
    KAngleList.append(X[0][0])
    KalmanList.append(K[0][0])
    KalmanList2.append(K[1][0])
    BiasList.append(X[1][0])
KAngleList = np.array(KAngleList)
KalmanList = np.array(KalmanList)
GAngleList = np.array(GAngleList)
AAngleList = np.array(AAngleList)
BiasList = np.array(BiasList)

plt.figure("kalmanfilter")
plt.subplot(231)
plt.plot(TimeList,KAngleList,'r--')
plt.plot(TimeList,RollC,'c')
plt.subplot(232)
plt.plot(TimeList,GAngleList,'g')
plt.subplot(233)
plt.plot(TimeList,AAngleList,'b')
plt.subplot(234)
plt.plot(TimeList,gryo_x,'y')
plt.subplot(235)
plt.plot(TimeList,BiasList,'y--')
plt.subplot(236)

plt.plot(TimeList,KalmanList, 'r--')
plt.plot(TimeList,K1C, 'c')
plt.plot(TimeList,KalmanList2, 'g--')
plt.plot(TimeList,K2C, 'k')
plt.show()

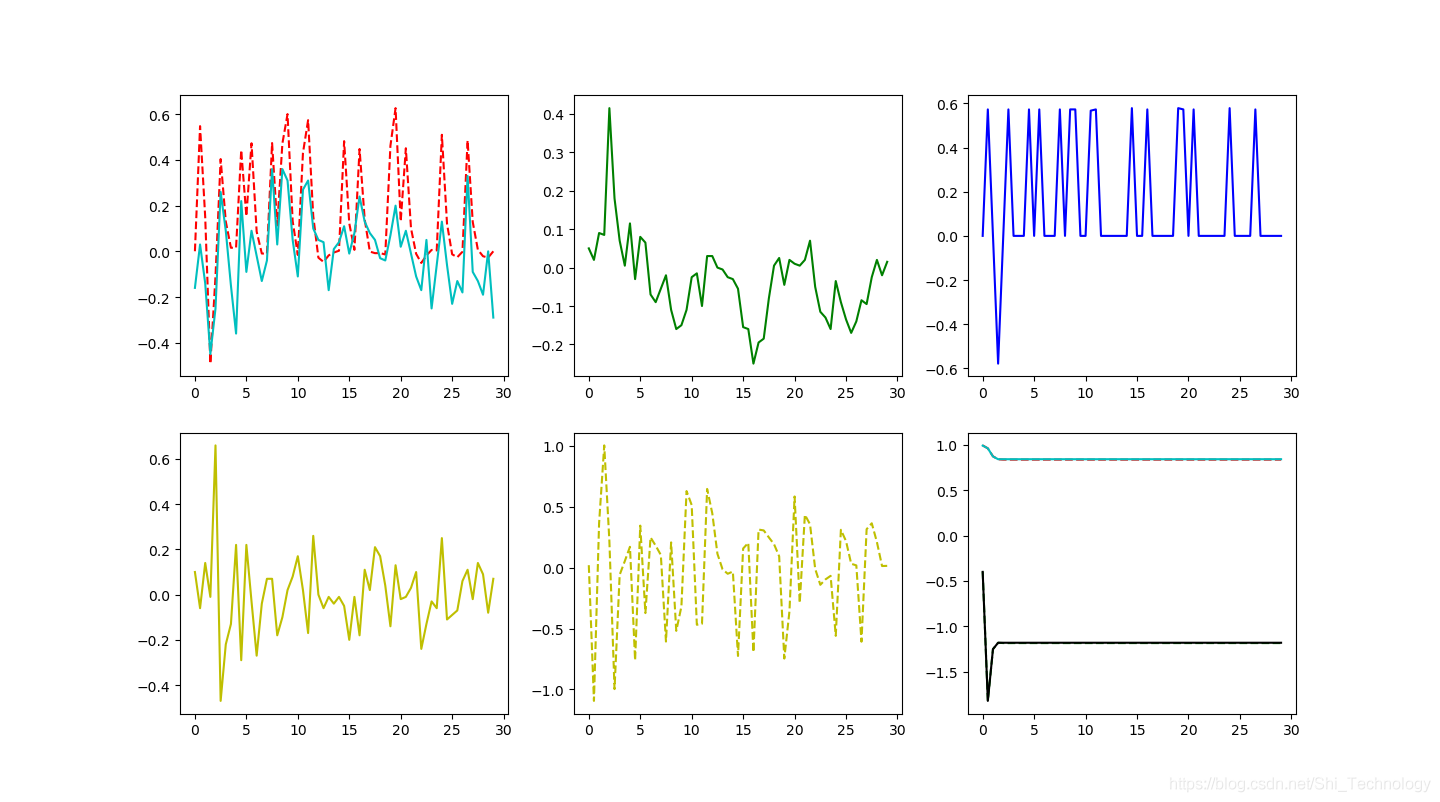
與C實現的結果進行對比：
第一張虛線是Python實現的卡爾曼濾波結果，天藍色是C語言實現版本結果；第二張是單純使用陀螺儀積分結果，第三張是單獨使用加速度解算結果；第四張是角速度；第六章實線是C語言計算出的卡爾曼增益，虛線是Python計算出的。兩者曲線基本重合，所以應該是沒問題的，但是爲什麼第一張濾波結果不同，估計是計算精度的問題。
结果对比

Reference

卡爾曼濾波演算法的推導以及C實現（這篇博文強烈推薦，說的特別詳細）：a-practical-approach-to-kalman-filter-and-how-to-implement-it
關於姿態角的加速度求解：靜態條件下三軸加速度求角度的演算法
卡爾曼濾波演算法的參數理解與推導？：卡爾曼濾波演算法的參數理解
Goldman公式的推導：Goldman公式的推導
機器人學導論[J.Craig]

MPU6050卡爾曼濾波解算姿態角

前言