c/c++ leetcode 二元樹和二元搜尋樹的最近公共祖先

236. 二元樹的最近公共祖先:

236. 二元樹的最近公共祖先

難度中等686

給定一個二元樹, 找到該樹中兩個指定節點的最近公共祖先。

百度百科中最近公共祖先的定義爲：「對於有根樹 T 的兩個結點 p、q，最近公共祖先表示爲一個結點 x，滿足 x 是 p、q 的祖先且 x 的深度儘可能大（一個節點也可以是它自己的祖先）。」

例如，給定如下二元樹: root = [3,5,1,6,2,0,8,null,null,7,4]

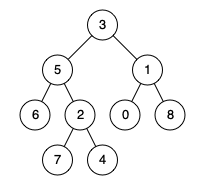
範例 1:

輸入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
輸出: 3
解釋: 節點 5 和節點 1 的最近公共祖先是節點 3。

範例 2:

輸入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
輸出: 5
解釋: 節點 5 和節點 4 的最近公共祖先是節點 5。因爲根據定義最近公共祖先節點可以爲節點本身。

解法:遞回

如果看不懂程式碼可以把每層root -> val 列印出來幫助理解

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		cout << root -> val << endl;
        if (root == NULL || root == p || q == root) return root;
 		

        TreeNode* left = lowestCommonAncestor(root -> left,p,q);
        TreeNode* right = lowestCommonAncestor(root -> right,p,q);

        return !left ? right : !right ? left : root;
    }
};

時空複雜度分析:

時間複雜度: 最壞情況下把整個二元樹遍歷一遍 爲O(N) N是 二元樹的節點個數;

空間複雜度: 最壞情況下開闢N個棧空間爲O(N);

235.二元搜尋樹的最近公共祖先

235. 二元搜尋樹的最近公共祖先

難度簡單350

給定一個二元搜尋樹, 找到該樹中兩個指定節點的最近公共祖先。

百度百科中最近公共祖先的定義爲：「對於有根樹 T 的兩個結點 p、q，最近公共祖先表示爲一個結點 x，滿足 x 是 p、q 的祖先且 x 的深度儘可能大（一個節點也可以是它自己的祖先）。」

例如，給定如下二元搜尋樹: root = [6,2,8,0,4,7,9,null,null,3,5]

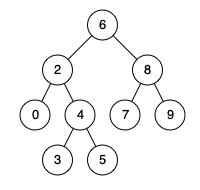
範例 1:

輸入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
輸出: 6 
解釋: 節點 2 和節點 8 的最近公共祖先是 6。

範例 2:

輸入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
輸出: 2
解釋: 節點 2 和節點 4 的最近公共祖先是 2, 因爲根據定義最近公共祖先節點可以爲節點本身。

解法一使用普通遞回

能用在二元樹上,當然也能用到 二元搜尋樹上,二元搜尋樹屬於二元樹,

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        cout << root -> val << endl;
        if (root == NULL || root == p || q == root) return root;
 		
		
        TreeNode* left = lowestCommonAncestor(root -> left,p,q);
        TreeNode* right = lowestCommonAncestor(root -> right,p,q);

        return !left ? right : !right ? left : root;
    }
};

解法二: 使用二元搜尋樹的特性進行遞回

根據 二元搜尋樹的右子樹大於根節點,左子樹小於根節點的特性減少遞回次數

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        cout << root -> val << endl;
        if (root == NULL || (root -> val  > p -> val && root -> val < q -> val) || 
        (root -> val  < p -> val && root -> val > q -> val) || root == p || root == q) 
            return root;
        TreeNode * left = NULL,* right = NULL;
        if (root -> val < p -> val && root -> val < q -> val )   
             right = lowestCommonAncestor(root -> right,p,q);

        if (root -> val > q -> val && root -> val > p -> val )   
             left = lowestCommonAncestor(root -> left,p,q);
       
        return !left ? right : !right ? left : root;
        
    }

時空複雜度分析:

時間複雜度: 最壞情況下把整個二元樹遍歷一遍 爲O(N) N是 二元樹的節點個數;

   return !left ? right : !right ? left : root;
    
}

#### 時空複雜度分析:

時間複雜度: 最壞情況下把整個二元樹遍歷一遍 爲O(N) N是 二元樹的節點個數;

空間複雜度:  最壞情況下開闢N個棧空間爲O(N);