技術文章 » r語言實現關聯分析--關聯規則挖掘（Apriori演算法） （r語言預測學習筆記）

r語言實現關聯分析--關聯規則挖掘（Apriori演算法） （r語言預測學習筆記）

2020-08-08 21:26:26

r語言實現關聯分析–關聯規則挖掘

關聯分析：

引子：
我們一般把一件事情發生，對另一間事情也會產生影響的關係叫做關聯。而關聯分析就是在大量數據中發現項集之間有趣的關聯和相關聯繫（形如「由於某些事件的發生而引起另外一些事件的發生」）。 我們的生活中有許多關聯，一個典型例子是購物籃分析。該過程通過發現顧客放入其購物籃中的不同商品之間的聯繫，分析顧客的購買習慣。通過了解哪些商品頻繁地被顧客同時購買，這種關聯的發現可以幫助零售商制定行銷策略。其他的應用還包括價目表設計、商品促銷、商品的排放和基於購買模式的顧客劃分。

關聯分析的基本概念：

關聯規則是指形如 x→y 的形式，x 和 y 分別成爲關聯規則的 前項 和 後項。關聯規則挖掘的數據是事務數據集，它包含事務ID和項的子集兩個屬性。（類似下面 下麪的數據框）
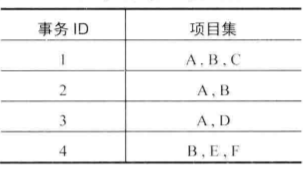
在这里插入图片描述
根據上面的數據介紹一些關聯分析涉及到的基本概念
項集：包含0個或多個項的集合，例如{A、B}，含有k個項就是k-項集。
關聯規則：形如A→B的關聯，其中A∩B非空。
支援度計數：包含特定項集的個數，由範例可知 σ(A→B)=2 表示同時包含AB的項集數爲2.
支援度：包含特定項集的個數佔總項集數的比值。
頻繁項集：滿足最小支援度的所有項集
置信度：用條件概率表示，c(A→B)=p(A|B) A發生的條件下B發生的概率.
期望置信度：在沒有任何條件影響的情況下，事件A出現的概率
提升度：關聯規則A→B下 A事件發生對B事件產生的影響程度

關聯分析有兩個目標：
1.發現頻繁項集（頻繁項集是滿足最小支援度要求的項集，它給出經常在一起出現的元素項）
2.發現關聯規則（關聯規則意味着元素項之間「如果…那麼…」的關係）

常用的關聯規則挖掘演算法有Aprior演算法
Apriori演算法是一種最有影響的挖掘布爾關聯規則頻繁項集的演算法。其核心是基於兩階段頻集思想的遞推演算法。Apriori演算法可挖掘出關聯規則

Apriori演算法

Apriori定律1：如果某個項集是頻繁的，那麼它的所有子集也是頻繁的
Apriori定律2：如果某個項集是非頻繁的，那麼它的所有超集也是非頻繁的
Apriori定律3：基於此，Apriori演算法從單元素項集開始，通過組合滿足最小支援度的項集來形成更大的集合

兩個步驟：1.通過迭代找出事務數據集中所有頻繁項集，即支援度不低於設定閾值的項集。 2.利用頻繁項集構造出滿足使用者最小置信度的關聯準則，利用支援度對候選項集進行剪枝。

此處以範例事務數據集演示手動計算過程，設定最小支援度閾值minsup=0.3.從生成c1開始，到不能找到任何頻繁k項集爲止，過程如下所示。

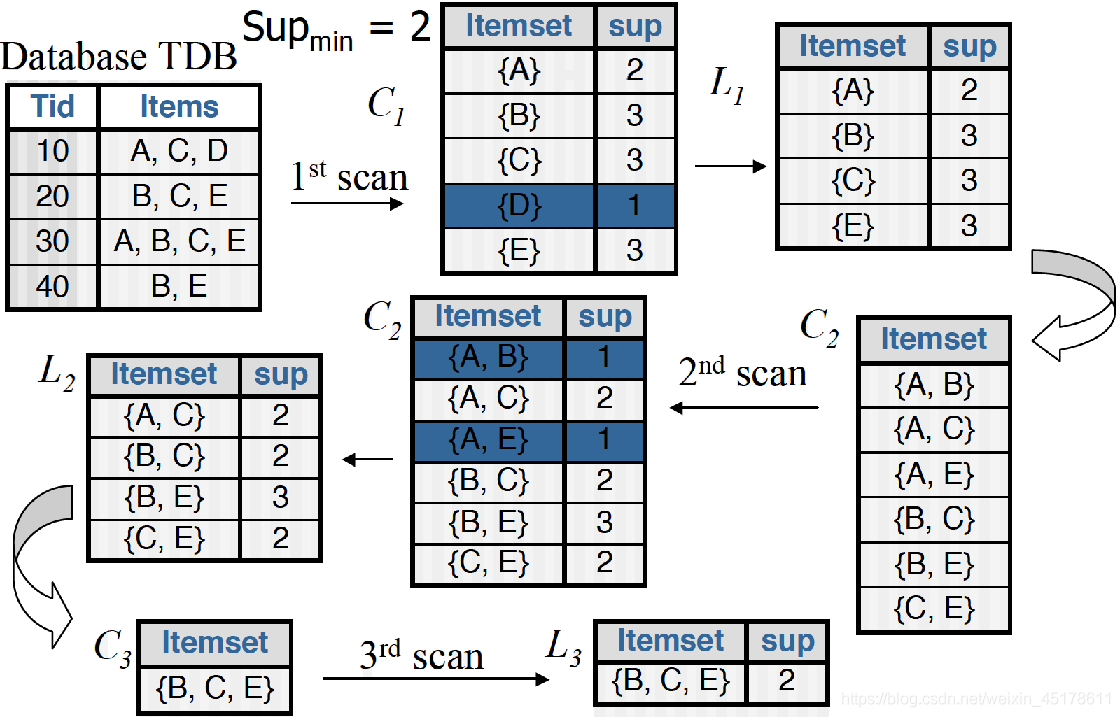
在这里插入图片描述
在第一次掃描（1st scan）中，minsup=2，{D}不符合要求，因此剪掉，生成頻繁1項集L1，L1自動鏈接生成候選2項集c2。L1中各項集只有一個項，因此兩兩組合。後面的操作與第一步操作類似。
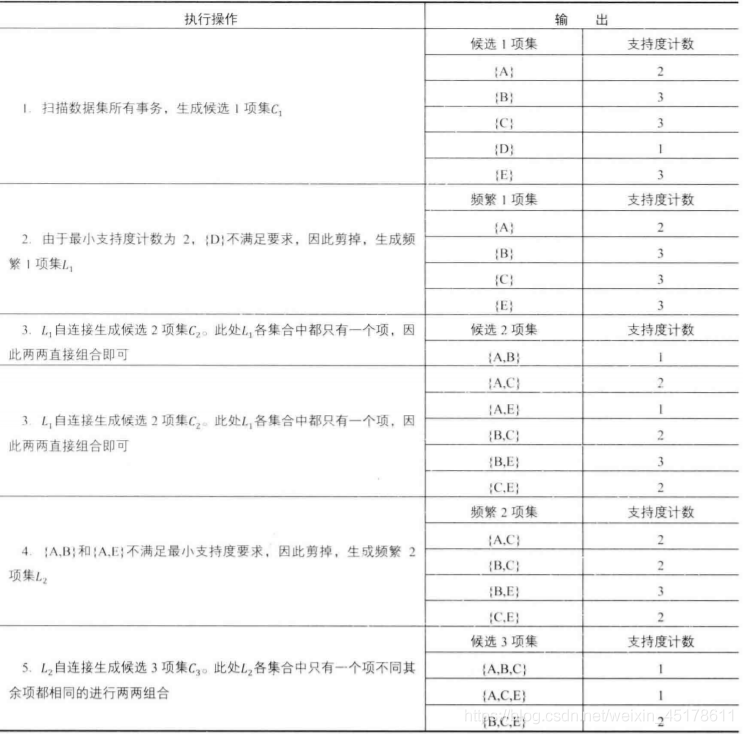
在这里插入图片描述
在这里插入图片描述
最終得到的頻繁項集 L3={B、C、E} 它的任何2項子集都是頻繁的。

此時便達到了關聯分析的第一個目標：發現頻繁項集。接着要尋找（構造）關聯規則

關聯規則：對每個頻繁項集L，產生L的非空真子集，對L的每個非空真子集S，若都能滿足置信度大於等於給定的最小置信度的情況下，即C(S→CS)≧min-conf，（CS表示S在L中的補集），那麼就是強關聯規則。。

對於L3，它的非空自己爲{B},{C},{E},{B,C},{B,E},{C,E},假設定信度min-conf=0.5，則獲得的關聯規則及置信度如下
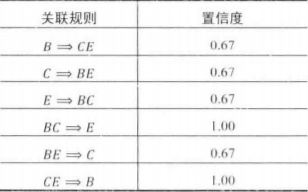
在这里插入图片描述
可見，置信度都大於最小置信水平，說明得到的關聯規則都是強關聯規則。

Apriori演算法流程圖：
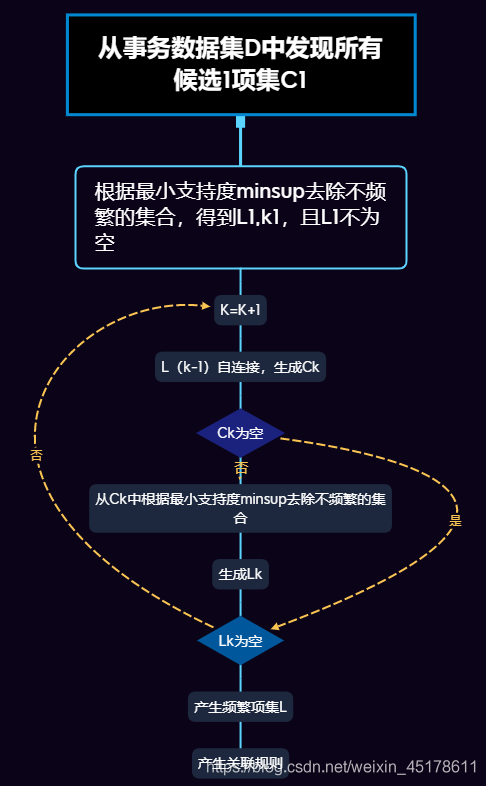
在这里插入图片描述

r語言實現Apriori演算法

r語言中，arules包主要用於挖掘頻繁項集和關聯規則，該包中的apriori函數可以實現這個演算法。
下面 下麪是函數定義及參數說明
函數定義：

apriori(data,parameter=NULL,appearance=NULL,control=NULL)

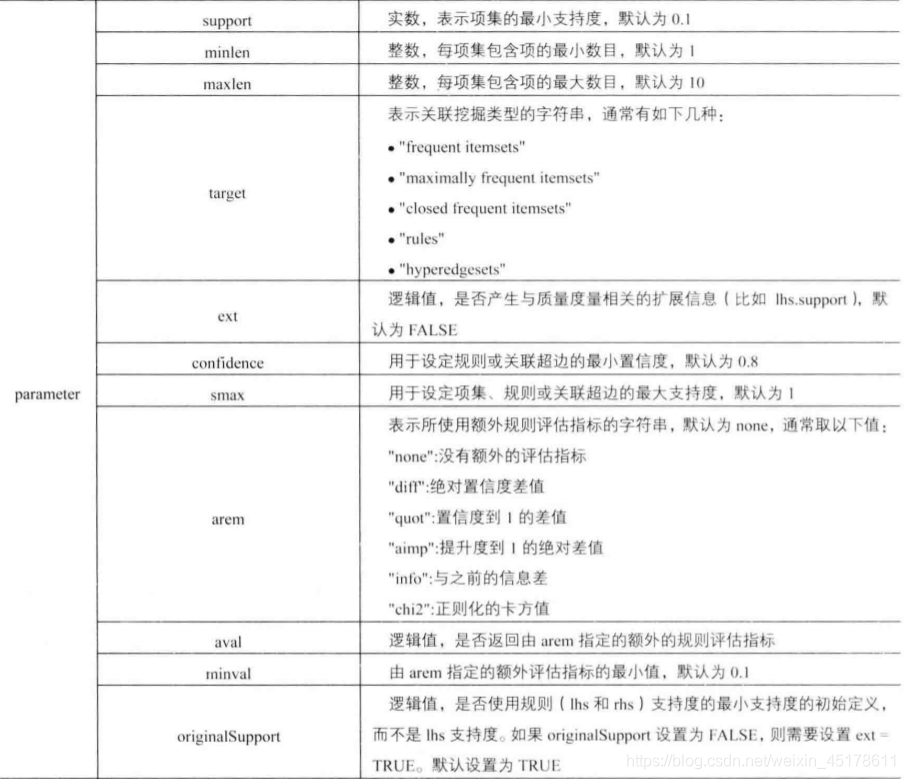
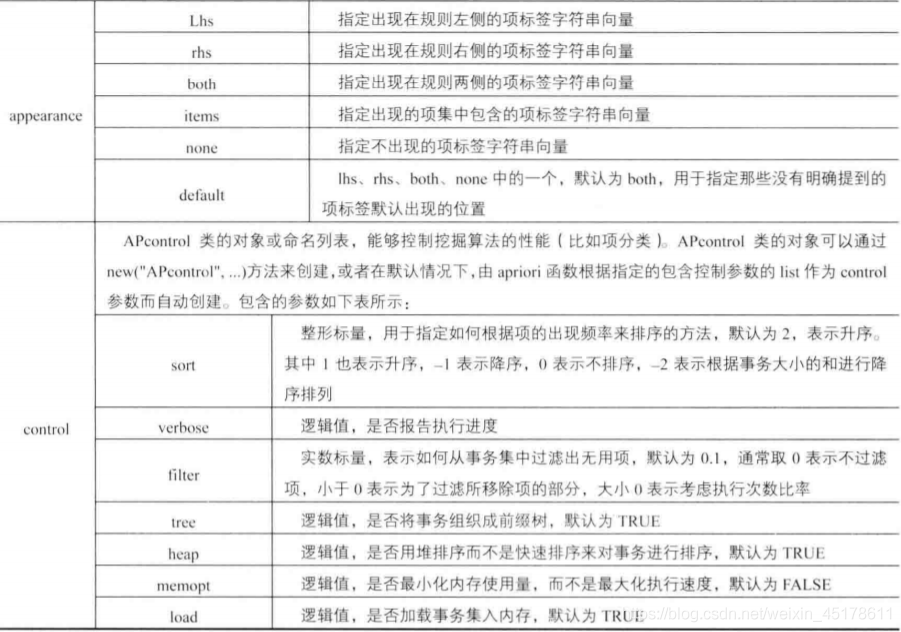
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
數據預處理（離散化數據）：
這裏使用AirPassengers數據集，將對應的乘客數據轉化爲環比值，

L<-NROW(AirPassengers)
ap.chain<-AirPassengers[2:L]/AirPassengers[1:(L-1)]
plot(ap.chain,pch=20)
lines(ap.chain)
abline(h=1.0,lty=2,col='red')

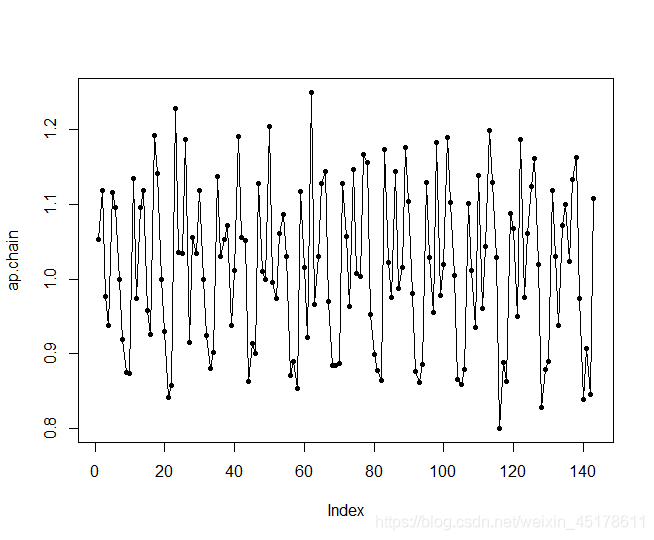
在这里插入图片描述
可以看出環比值圍繞着1.0上下波動，並由一定的週期性
再進行離散化處理，將環比值按分佈區間等分成4份。程式碼如下：

> ap.chain.dez<-cut(ap.chain,breaks=4,include.lowest=T)
> ap.chain.lab<-cut(ap.chain,breaks=4,include.lowest=T,labels=c("A","B","C","D"))
> out<-data.frame(dez=ap.chain.dez,lab=ap.chain.lab,chain=ap.chain)
> head(out)
           dez lab     chain
1  (1.02,1.14]   C 1.0535714
2  (1.02,1.14]   C 1.1186441
3 (0.913,1.02]   B 0.9772727
4 (0.913,1.02]   B 0.9379845
5  (1.02,1.14]   C 1.1157025
6  (1.02,1.14]   C 1.0962963

對下一週期預測時，需考慮近十期的環比情況，因此按十個月的視窗週期，重新構建數據集，使用

Apriori演算法提取規則：
#構建數據集
>winSize=10
>conMatrix=t(mapply(function(i)ap.chain.lab[i:(i+winSize-1)],
                                 1:(NROW(ap.chain)-winSize+1)))
#由於數據都是按時間先後順序整理的，因此用前百分之八十提取規則，後百分之二十驗證規則
>partVal<-round(dim(conMatrix)[1]*0.8,0)
>trainData<-data.frame(conMatrix[1:partVal,])
>validData<-conMatrix[(partVal+1):dim(conMatrix)[1],]
#使用Apriori提取規則
>library(arules)
>apriori.obj<-apriori(trainData,parameter=list(supp=0.1,conf=0.5,target="rules"),appearance=list(rhs=c("X10=A","X10=B","X10=C","X10=D"),default="lhs"))
>inspect(apriori.obj)
  lhs            rhs     support   confidence coverage  lift     count
[1] {X9=D}      => {X10=B} 0.1028037 0.6111111  0.1682243 1.868254 11   
[2] {X4=A}      => {X10=B} 0.1308411 0.6086957  0.2149533 1.860870 14   
[3] {X5=A}      => {X10=B} 0.1401869 0.6521739  0.2149533 1.993789 15   
[4] {X7=A}      => {X10=C} 0.1121495 0.5217391  0.2149533 1.800842 12   
[5] {X9=A}      => {X10=A} 0.1214953 0.5652174  0.2149533 2.629490 13   
[6] {X4=B,X9=A} => {X10=A} 0.1028037 0.9166667  0.1121495 4.264493 11   
> inspect(apriori.obj[which.max(quality(apriori.obj)$lift)])
    lhs            rhs     support   confidence coverage  lift     count
[1] {X4=B,X9=A} => {X10=A} 0.1028037 0.9166667  0.1121495 4.264493 11

由程式碼所示，insepct函數可檢視計算得出的結果，包含三個屬性，分別是支援度，置信度和提升度，其中支援度最高的一條規則是 {X4=B,X9=A} => {X10=A} ，我們通過驗證集validData進行驗證

> rulesData=as(apriori.obj,"data.frame")
> rulesData[which.max(rulesData$lift),]
                   rules   support confidence  coverage     lift count
6 {X4=B,X9=A} => {X10=A} 0.1028037  0.9166667 0.1121495 4.264493    11
> tmp<-validData[validData[,4]=='B' & validData[,9]=='A',10]
> hitRate<-paste(NROW(tmp=='A')/NROW(tmp)*100,"%",sep="")
> hitRate
[1] "100%"

可以看出此條規則對未來20個月的預測全部命中。例如若要預測1960年11月的環比值，根據規則，當同年5月環比值1.02位於【0.913，1.02】區間，並且同年十月環比值0.91位於【0.8，0.913】區間時，則可以有效預測11月份環比值介於0.8~0.913之間。

缺：關聯分析視覺化