(二)背景知識 -- 4 神經概率語言模型
2020-08-08 21:59:39
4. 神經概率語言模型
對應上一小節 概率模型函數化,神經概率語言模型即用「神經網路」構建「函數」。
4.1 詞向量
對詞典中任意詞,指定一個固定長度的實值向量 。則,稱爲的詞向量,爲詞向量的長度。
詞向量存在兩種表示方法:
(1) One-hot Representation
用維度爲字典長度的向量表示一個詞,僅一個分量爲1,其餘爲0。
缺點:容易導致維度災難,且無法很好地刻畫詞與詞之間的關係。
(2) Distributed Representation
每個詞對映爲固定長度的短向量,通過刻畫兩個向量之間的距離來刻畫兩個向量之間的相似度。
4.2 網路結構
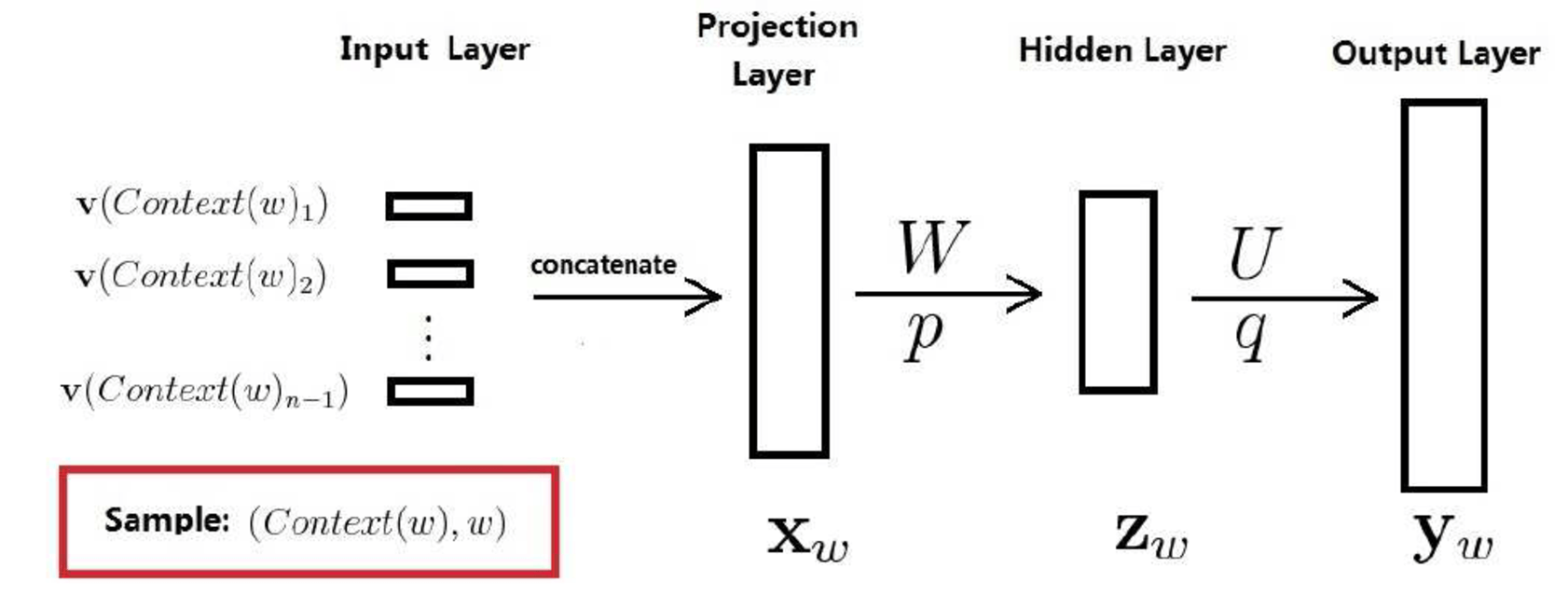
其中,
- 訓練樣本
是語料C中的每一個詞,取爲其前面個詞。 - 投影層向量
將該訓練樣本的前個詞的詞向量首尾相接,拼接在一起構成。
的長度爲,爲詞向量長度。 - 隱藏層向量 :
- 輸出層向量 :
維度爲,即,詞典中詞的個數。
注:在對做Softmax歸一化後,的分量表示當前詞是的概率。
對於該神經網路,其參數包括:「詞向量以及「神經網路參數」。一旦確定了這些參數,就相當於確定了「函數」的參數,也就相當於知道了參數,繼而能求得整個句子的概率。
4.3 優缺點
相比於N-gram模型,神經概率語言模型具有以下優點:
(1) 詞與詞之間的相似度可以通過詞向量來體現。
(2) 基於詞向量的模型自帶「平滑化」功能,無需額外處理。因爲公式 不可能爲0。
神經概率語言模型的主要缺點是計算量太大,各參數量級分別爲:
(1) 投影層節點數=上下文詞數量*詞向量維度。上下文數量通常不超過,詞向量維度在量級。
(2) 隱層節點數在量級,
(3) 輸出層節點數爲詞典大小,在量級。
因此,對於神經概率語言模型,其主要的計算集中在「隱層和輸出層之間的矩陣運算」和「輸出層上的Softmax歸一化運算」。
考慮到語言模型對語料庫中的每一個詞都要進行訓練,而語料庫通常有以上的詞數,無法承擔該計算量。因此,需要做進一步的優化。