1.第幾天

2000年的1月1日，是那一年的第1天。
那麼，2000年的5月4日，是那一年的第幾天？

注意：需要提交的是一個整數，不要填寫任何多餘內容。

1.1思路

簡單題，要注意的只有2000是閏年，2月 29天

1.2原始碼

#include<stdio.h>
int main()
{
	printf("%d",31+29+31+30+4);
	return 0;

2.明碼

漢字的字形存在於字型檔中，即便在今天，16點陣的字型檔也仍然使用廣泛。
16點陣的字型檔把每個漢字看成是16x16個畫素資訊。並把這些資訊記錄在位元組中。

一個位元組可以儲存8位元資訊，用32個位元組就可以存一個漢字的字形了。
把每個位元組轉爲2進製表示，1表示墨跡，0表示底色。每行2個位元組，
一共16行，佈局是：

第1位元組，第2位元組
第3位元組，第4位元組
....
第31位元組, 第32位元組

這道題目是給你一段多個漢字組成的資訊，每個漢字用32個位元組表示，這裏給出了位元組作爲有符號整數的值。

題目的要求隱藏在這些資訊中。你的任務是復原這些漢字的字形，從中看出題目的要求，並根據要求填寫答案。

這段資訊是（一共10個漢字）：

4 0 4 0 4 0 4 32 -1 -16 4 32 4 32 4 32 4 32 4 32 8 32 8 32 16 34 16 34 32 30 -64 0 
16 64 16 64 34 68 127 126 66 -124 67 4 66 4 66 -124 126 100 66 36 66 4 66 4 66 4 126 4 66 40 0 16 
4 0 4 0 4 0 4 32 -1 -16 4 32 4 32 4 32 4 32 4 32 8 32 8 32 16 34 16 34 32 30 -64 0 
0 -128 64 -128 48 -128 17 8 1 -4 2 8 8 80 16 64 32 64 -32 64 32 -96 32 -96 33 16 34 8 36 14 40 4 
4 0 3 0 1 0 0 4 -1 -2 4 0 4 16 7 -8 4 16 4 16 4 16 8 16 8 16 16 16 32 -96 64 64 
16 64 20 72 62 -4 73 32 5 16 1 0 63 -8 1 0 -1 -2 0 64 0 80 63 -8 8 64 4 64 1 64 0 -128 
0 16 63 -8 1 0 1 0 1 0 1 4 -1 -2 1 0 1 0 1 0 1 0 1 0 1 0 1 0 5 0 2 0 
2 0 2 0 7 -16 8 32 24 64 37 -128 2 -128 12 -128 113 -4 2 8 12 16 18 32 33 -64 1 0 14 0 112 0 
1 0 1 0 1 0 9 32 9 16 17 12 17 4 33 16 65 16 1 32 1 64 0 -128 1 0 2 0 12 0 112 0 
0 0 0 0 7 -16 24 24 48 12 56 12 0 56 0 -32 0 -64 0 -128 0 0 0 0 1 -128 3 -64 1 -128 0 0

注意：需要提交的是一個整數，不要填寫任何多餘內容。

2.1思路

看懂題目的意思很重要，一個漢字有32位元組，每個漢字16x16畫素資訊，就是16x2（2就代表位元組），共16行列印出來。
1.主函數可以通過雙重for回圈每次將兩個位元組輸入，然後通過建立的函數列印出來
2.函數將 10 進位制數轉化爲 2 進位制數，然後通過for回圈列印出來。
3.還有要注意的一點：負數2進位制的求法（正數第一位是0），如果是負數，則直接令第一位爲1

2.2 二進制求法

如 X
第一位：1  其他7位 128+x的2進位制
正數二進制能表示範圍（0 000 0001 ~ 0 111 1111）即1~127
負數二進制能能表示的範圍（1 000  0001 ~ 1 111 1111）即-127~-1

2.3原始碼

#include<stdio.h>
#include<math.h>

int out(int t[],int a,int b){ 
 
	for(int i=7;i>0;i--)
	{
		if(a<0){
			a=a+128;
			t[0]=1;	
		}
		else{
			a=a;
			t[0]=0;
		} 
		t[i]=a%2;
		a/=2;
	}
	for(int i=0;i<=7;i++)printf("%c",t[i]? '*':' ');
	for(int i=7;i>0;i--)
	{
		if(b<0){
			b=b+128;
			t[0]=1;

		}
		else{
			a=a;
			t[0]=0;
		}
		
		t[i]=b%2;
		b/=2;
	}
	for(int i=0;i<=7;i++)printf("%c",t[i]? '*':' ');
	printf("\n");

}
int main(){
	int sum=1;
	int a,b;
	int t[8];
	for(int i=0;i<10;i++){
		for(int j=0;j<16;j++){
			scanf("%d %d",&a,&b);
			out(t,a,b);
		
		}
	}
	for(int i=0;i<9;i++)
		sum*=9;
	printf("%d",sum);
}

3.乘積尾零

如下的10行數據，每行有10個整數，請你求出它們的乘積的末尾有多少個零？

5650 4542 3554 473 946 4114 3871 9073 90 4329 
2758 7949 6113 5659 5245 7432 3051 4434 6704 3594 
9937 1173 6866 3397 4759 7557 3070 2287 1453 9899 
1486 5722 3135 1170 4014 5510 5120 729 2880 9019 
2049 698 4582 4346 4427 646 9742 7340 1230 7683 
5693 7015 6887 7381 4172 4341 2909 2027 7355 5649 
6701 6645 1671 5978 2704 9926 295 3125 3878 6785 
2066 4247 4800 1578 6652 4616 1113 6205 3264 2915 
3966 5291 2904 1285 2193 1428 2265 8730 9436 7074 
689 5510 8243 6114 337 4096 8199 7313 3685 211

注意：需要提交的是一個整數，表示末尾零的個數。不要填寫任何多餘內容。

3.1思路

由2x5=10，可以知道，每一個0都可以2,5組成
則只要統計2,5的個數就行了。

3.2原始碼

#include<stdio.h>
int main(){
	int sum;
	int a=0,b=0;
		for(int j=0;j<100;j++){
			scanf("%d",&sum);
			while(sum%5==0){
				a++;
				sum/=5;
				
			}
			while(sum%2==0){
				b++;
				sum/=2;
			}
			
		}
	printf("%d",a>=b?b:a);
}

4.測試次數

x星球的居民脾氣不太好，但好在他們生氣的時候唯一的異常舉動是：摔手機。
各大廠商也就紛紛推出各種耐摔型手機。x星球的質監局規定了手機必須經過耐摔測試，並且評定出一個耐摔指數來，之後才允許上市流通。

x星球有很多高聳入雲的高塔，剛好可以用來做耐摔測試。塔的每一層高度都是一樣的，與地球上稍有不同的是，他們的第一層不是地面，而是相當於我們的2樓。

如果手機從第7層扔下去沒摔壞，但第8層摔壞了，則手機耐摔指數=7。
特別地，如果手機從第1層扔下去就壞了，則耐摔指數=0。
如果到了塔的最高層第n層扔沒摔壞，則耐摔指數=n

爲了減少測試次數，從每個廠家抽樣3部手機參加測試。

某次測試的塔高爲1000層，如果我們總是採用最佳策略，在最壞的運氣下最多需要測試多少次才能纔能確定手機的耐摔指數呢？

請填寫這個最多測試次數。

注意：需要填寫的是一個整數，不要填寫任何多餘內容。

4.1思路

最佳策略：就是測位於所要測的塔中間層
比如： 3層
從中間測只要測2次，而在1,3層，則要測3次。
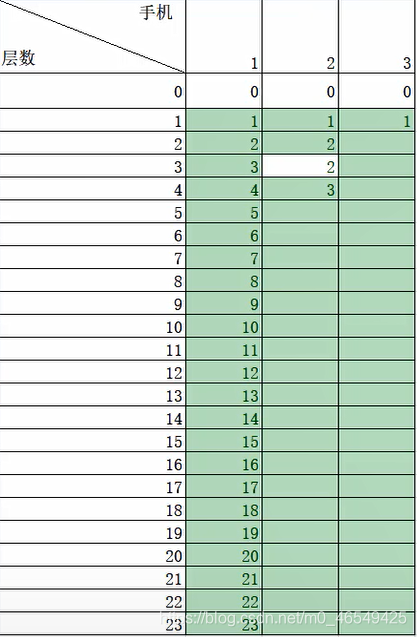
在这里插入图片描述

所謂最壞運氣：(測每層最多要幾次)
比如：
共四層：
1.在只有一部手機的情況下，如果從高層開始測的話，摔壞了，就沒法知道手機的耐摔指數，所以只能從1層開始，逐漸往上測，這樣既能知道耐摔指數，又可以知道測試的次數。
當然測試次數是最主要的，由上面的圖，我們就可以知道測試次數跟層數是相等的。
表示形式就是（1,1）=1，（1,2）=2。含義就是1部手機測1層的次數，1部手機測2層的次數、
2.有兩部手機
從1層測起：
壞：另一部手機不用測，就能知道測試次數爲1次。
好：2部手機測另外三層。（2,3）次+1
從2層測起：
壞：另一部手機，測1層測（1,1）次+1
好：兩部手機，測兩層測（2,2）次+1
從3層測起：
壞：另一部手機，測兩層，測（1,2）次+1
好：兩部手機，測1層，測（2,1）次+1
從第4層測起：
壞：另一部手機，測3層，測（1,3）次+1
好：兩部手機，不用繼續測了，就測了1次
爲什麼要+1，因爲本身就測了一次

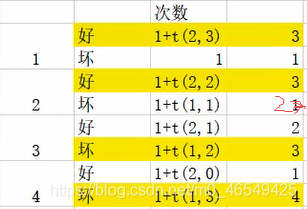
在这里插入图片描述
然後前面說的最佳策略：就是在這個圖中的2,3層，測試次數也應該在裏面，然後題目也是求測試次數，思路大概就是這樣。
上面的也可以簡化爲：
f1[n]=n
f2[n]=min(for i in n max( 1+f2[n-i] , 1+f1[i-i] )
f3[n]=min(for i in n max( 1+f3[n-i]) , 1+f2[i-1] )

4.2原始碼

#include<stdio.h>
#include<limits.h>
const int n=1000;
int f1[n+1],f2[n+1],f3[n+1];    
/*
	f1[n+1]表示的就是1部手機，測n層
		如f1[1]=1,f1[2]=2 
	*/
int max(int a,int b){
	if(a>b)
		return a;
	else
		return b;
}
int min(int a,int b){
	if(a<b)
		return a;
	else
		return b;
}
int main(){
	for(int i=1;i<=n;i++){       
	 //求出一部手機測的次數
		f1[i]=i;
	}
	for(int i=1;i<=n;i++){
		int ans=INT_MAX;
		for(int j=1;j<=i;j++){
			int _max=1+max(f2[i-j],f1[j-1]);     
			//用到了max()函數，求兩部手機測每層要花的次數 
			ans=min(ans,_max);			
		}
		f2[i]=ans;
	}
		for(int i=1;i<=n;i++){
		int ans=INT_MAX;
		for(int j=1;j<=i;j++){
			int _max=1+max(f3[i-j],f2[j-1]);
			ans=min(ans,_max);			
		}
		f3[i]=ans;
	}
	printf("%d",f3[n]);
}

5.快速排序

以下程式碼可以從陣列a[]中找出第k小的元素。

它使用了類似快速排序中的分治演算法，期望時間複雜度是O(N)的。

請仔細閱讀分析原始碼，填寫劃線部分缺失的內容。

#include <stdio.h>

int quick_select(int a[], int l, int r, int k) {
	int p = rand() % (r - l + 1) + l;
	int x = a[p];
	{int t = a[p]; a[p] = a[r]; a[r] = t;}
	int i = l, j = r;
	while(i < j) {
		while(i < j && a[i] < x) i++;
		if(i < j) {
			a[j] = a[i];
			j--;
		}
		while(i < j && a[j] > x) j--;
		if(i < j) {
			a[i] = a[j];
			i++;
		}
	}
	a[i] = x;
	p = i;
	if(i - l + 1 == k) return a[i];
	if(i - l + 1 < k) return quick_select( _____________________________ ); //填空
	else return quick_select(a, l, i - 1, k);
}
	
int main()
{
	int a[] = {1, 4, 2, 8, 5, 7, 23, 58, 16, 27, 55, 13, 26, 24, 12};
	printf("%d\n", quick_select(a, 0, 14, 5));
	return 0;
}

注意：只填寫劃線部分缺少的程式碼，不要抄寫已經存在的程式碼或符號。

5.1思路

快排的思想：就是先找一個數作爲基準，然後從陣列的右邊 ( j - - )找一個比基準小的，從陣列的左邊( i + + )找一個比基準大的，然後交換這兩個數。最後 i = = j,最後就把基準數放在這個位置。
這個題目的話，找出第 K 小的數，看題目：
if(i - l + 1 == k) return a[i]; ,( i - l + 1)表示的就是第幾個元素，所以這句話就是 i 等於第K小的數
if(i - l + 1 < k) return quick_select( )；：這句話就是K比確定的基準 I 還要大，所以K在 i 的右邊。並且位置是K-( i - l + 1 ),爲什麼是這樣呢，還得從快排的思想說起，快排就是確定一個個基準，把數分成很多分，然後交換數的順序。當只有一個基準時，則只有兩部分，所以左邊的佔取了一些位置，所以需要減去左邊( i - l + 1)

5.2答案

( a , i +1 , r , k - ( i - l + 1 ) )

6.遞增三元組

給定三個整數陣列

A = [A1, A2, ... AN], 
B = [B1, B2, ... BN], 
C = [C1, C2, ... CN]，

請你統計有多少個三元組(i, j, k) 滿足：

1. 1 <= i, j, k <= N  
2. Ai < Bj < Ck

【輸入格式】

第一行包含一個整數N。
第二行包含N個整數A1, A2, ... AN。
第三行包含N個整數B1, B2, ... BN。
第四行包含N個整數C1, C2, ... CN。

對於30%的數據，1 <= N <= 100  
對於60%的數據，1 <= N <= 1000 
對於100%的數據，1 <= N <= 100000 0 <= Ai, Bi, Ci <= 100000

【輸出格式】 =+
一個整數表示答案

【樣例輸入】

【樣例輸出】

資源約定：
峯值記憶體消耗（含虛擬機器） < 256M
CPU消耗 < 1000ms

請嚴格按要求輸出，不要畫蛇添足地列印類似：「請您輸入…」的多餘內容。

注意：

main函數需要返回0;
只使用ANSI C/ANSI C++ 標準;
不要呼叫依賴於編譯環境或操作系統的特殊函數。
所有依賴的函數必須明確地在原始檔中 #include <xxx>
不能通過工程設定而省略常用標頭檔案。

提交程式時，注意選擇所期望的語言型別和編譯器型別。

6.1思路

這道題如果用暴力搜尋其實挺簡單的，就是先給三個陣列排序，然後用三重for回圈判斷滿足條件的個數，但是這樣只能得30分。
下面下麪有一種更好的辦法：
就是把b陣列當成基準，分別從a,c陣列中找比b陣列小的數和比b陣列大的數，然後確定個數。

6.2原始碼

#include<stdio.h>
const int N=100001;
void sort(int a[],int n){
	int t;
	for(int i=0;i<n-1;i++){
		for(int j=i+1;j<n;j++){
			if(a[i]>a[j]){
				t=a[i];
				a[i]=a[j];
				a[j]=t;
			}
		}
	}
}
int main(){
	int a[N],b[N],c[N];
	int n;
	long long ans=0;
	scanf("%d",&n);
	for(int i=0;i<n;i++)
		scanf("%d",&a[i]);
		
	for(int i=0;i<n;i++)
		scanf("%d",&b[i]);
		
	for(int i=0;i<n;i++)
		scanf("%d",&c[i]);
		
		sort(a,n);  //a,b,c陣列從小到大排序 
		sort(b,n);
		sort(c,n);
		
		int p=0,q=0;   //來統計以 b陣列爲基準，p:比b陣列小的數的個數，(n-q):比b陣列大的數的個數	
	for(int i=0;i<n;i++){
		while(p<n&&a[p]<b[i])   p++;
		while(q<n&&c[q]<=b[i])  q++;
		ans+=( (long long) p* (n-q) );
	}
	printf("%lld\n",ans);
}

7.螺旋折線

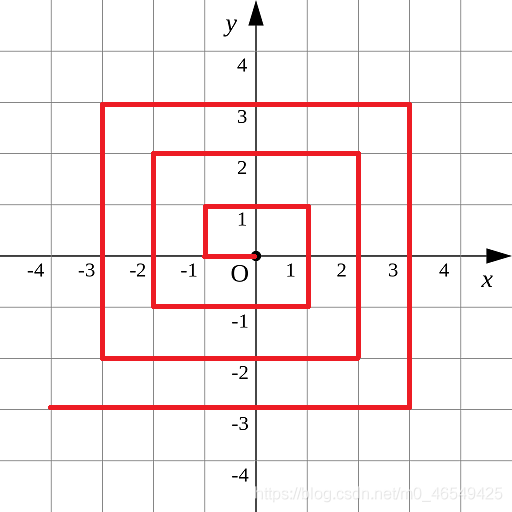
在这里插入图片描述

如圖p1.png所示的螺旋折線經過平面上所有整點恰好一次。
對於整點(X, Y)，我們定義它到原點的距離dis(X, Y)是從原點到(X, Y)的螺旋折線段的長度。

例如dis(0, 1)=3, dis(-2, -1)=9

給出整點座標(X, Y)，你能計算出dis(X, Y)嗎？

【輸入格式】

X和Y  
對於40%的數據，-1000 <= X, Y <= 1000  
對於70%的數據，-100000 <= X， Y <= 100000  
對於100%的數據, -1000000000 <= X, Y <= 1000000000

【輸出格式】

輸出dis(X, Y)

【樣例輸入】

0 1

【樣例輸出】

資源約定：

峯值記憶體消耗（含虛擬機器） < 256M
CPU消耗  < 1000ms

請嚴格按要求輸出，不要畫蛇添足地列印類似：「請您輸入…」的多餘內容。

注意：

main函數需要返回0;
只使用ANSI C/ANSI C++ 標準;
不要呼叫依賴於編譯環境或操作系統的特殊函數。
所有依賴的函數必須明確地在原始檔中 #include <xxx>
不能通過工程設定而省略常用標頭檔案。

提交程式時，注意選擇所期望的語言型別和編譯器型別。

7.1思路

將圖中（1,1）（2,2），（3,3）作爲一圈結束的標誌
則可以發現

 2 6 10
 4 8 12

可以構成等差數列把這個分爲兩部分（就是兩個相同的等差數列）
則可以形成 a0=1,d=1，n爲圈數*2的等差數列

 sum(1,2*n,1)*2-d
 這個就是等差數列求和公式

7.2原始碼

#include<stdio.h>
#include<stdlib.h>
#define sum(a0,n,d)  ( 2*a0 +((n)-1) *(d))* (n) /2 //等差數列求和
typedef long long LL;
int main(){
	LL x,y;
	scanf("%d %d",&x,&y);
	LL d=0;//距離 如距離點（2,2） 
	LL n=0;//第幾圈 (3,3)第3圈 
	if(y>0 && abs(x)<=y){  //就是第n圈中最上面平行x軸的直線
		n=y;
		d=y-x+2*y;
	}
	else if(x>0 && abs(y)<=x){//第n圈中，最右邊的那條線 
		n=x;
		d=x+y;
	}
	else if(y<=0 && x>=y-1 && x<=-y ){   //最底下的那條線，距離n-1圈更近 
		n=-y;
		d=-(-y-x);      //退回上一圈 
	}
	else if(x<0&& y>=x+1 && y<=-x){
		n=-x-1;
		d=-(y-x-1-2*x-1);   
	}
	printf("%d\n",sum(1,2*n,1)*2-d );      //n爲什麼*2？  因爲第三圈有6個格子 
	return 0;
}

8.日誌統計

小明維護着一個程式設計師論壇。現在他收集了一份"點贊"日誌，日誌共有N行。其中每一行的格式是：

ts id  

表示在ts時刻編號id的貼文收到一個"贊"。

現在小明想統計有哪些貼文曾經是"熱帖"。如果一個貼文曾在任意一個長度爲D的時間段內收到不少於K個贊，小明就認爲這個貼文曾是"熱帖"。

具體來說，如果存在某個時刻T滿足該帖在[T, T+D)這段時間內(注意是左閉右開區間)收到不少於K個贊，該帖就曾是"熱帖"。

給定日誌，請你幫助小明統計出所有曾是"熱帖"的貼文編號。

【輸入格式】
第一行包含三個整數N、D和K。  
以下N行每行一條日誌，包含兩個整數ts和id。  

對於50%的數據，1 <= K <= N <= 1000  
對於100%的數據，1 <= K <= N <= 100000 0 <= ts <= 100000 0 <= id <= 100000

【輸出格式】

按從小到大的順序輸出熱帖id。每個id一行。

【輸入樣例】

【輸出樣例】

1  
3

資源約定：

峯值記憶體消耗（含虛擬機器） < 256M
CPU消耗  < 1000ms

請嚴格按要求輸出，不要畫蛇添足地列印類似：「請您輸入…」的多餘內容。

注意：

main函數需要返回0;
只使用ANSI C/ANSI C++ 標準;
不要呼叫依賴於編譯環境或操作系統的特殊函數。
所有依賴的函數必須明確地在原始檔中 #include <xxx>
不能通過工程設定而省略常用標頭檔案。

提交程式時，注意選擇所期望的語言型別和編譯器型別。

8.1思路

詞取法

8.2原始碼

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
 
int n,d,k;
const int maxn=1e5+5;
vector<int> thing[maxn];
 
bool judge(int id)
{
	int len=thing[id].size();
	if(len<k)
		return false;
	sort(thing[id],thing[id]+len);
	int start=0;int end=0;
	int cnt=0;
	while(start<=end && end<len)
	{
		cnt++;
		if(cnt>=k)
		{
			if(thing[id][end]-thing[id][start]<d) //注意是小於(題中說是前閉後開區間 
				return true;
			else  //如果if語句不成立，那麼你再去後移end，也是不符要求的，所以該後移start了 
			{
				cnt--;
				start++;
			} 
		}
		end++;
	} 
	return false;
}  
 
int main()
{
	cin>>n>>d>>k;
	for(int i=1;i<=n;i++)
	{
		int ts,id;
		cin>>ts>>id;
		thing[id].push_back(ts);
	}
 
    int n_things = thing.size(); //取vector的長度，即有多少個id
    for(int id=1;id<=n_things;i++)
    {
        if(judge(id))
            cout<<id<<endl;
    }
    return 0;
}

9.全球變暖

你有一張某海域NxN畫素的照片，".「表示海洋、」#"表示陸地，如下所示：

.......
.##....
.##....
....##.
..####.
...###.
.......

其中"上下左右"四個方向上連在一起的一片陸地組成一座島嶼。例如上圖就有2座島嶼。

由於全球變暖導致了海面上升，科學家預測未來幾十年，島嶼邊緣一個畫素的範圍會被海水淹沒。具體來說如果一塊陸地畫素與海洋相鄰(上下左右四個相鄰畫素中有海洋)，它就會被淹沒。

例如上圖中的海域未來會變成如下樣子：

.......
.......
.......
.......
....#..
.......
.......

請你計算：依照科學家的預測，照片中有多少島嶼會被完全淹沒。

【輸入格式】

第一行包含一個整數N。  (1 <= N <= 1000)  
以下N行N列代表一張海域照片。  

照片保證第1行、第1列、第N行、第N列的畫素都是海洋。

【輸出格式】

一個整數表示答案。

【輸入樣例】

7 
.......
.##....
.##....
....##.
..####.
...###.
.......

【輸出樣例】

資源約定：

峯值記憶體消耗（含虛擬機器） < 256M
CPU消耗  < 1000ms

請嚴格按要求輸出，不要畫蛇添足地列印類似：「請您輸入…」的多餘內容。

注意：

main函數需要返回0;
只使用ANSI C/ANSI C++ 標準;
不要呼叫依賴於編譯環境或操作系統的特殊函數。
所有依賴的函數必須明確地在原始檔中 #include <xxx>
不能通過工程設定而省略常用標頭檔案。

提交程式時，注意選擇所期望的語言型別和編譯器型別。

9.1思路

使用DFS對陸地進行搜尋，並且對每個點進行判定，如果這個點被淹沒了，那麼就記錄爲1，反之記錄爲2，如果一個點的周圍已經有2或者3的時候，那麼這個點就記錄爲3，這樣做的目的是爲了方便尋找沒有被淹沒的島嶼個數。

9.2原始碼

#include <iostream>
#include <math.h>
#include <stdio.h>
#include <queue>
#define N 1005
using namespace std;
char m[N][N];
int n,book[N][N],sum;
int next[4][2] = {
    {1,0},
    {0,1},
    {-1,0},
    {0,-1}
};
//判斷當前搜尋的點，並改變在book中的標記
void check(int x, int y)
{
    int i,tx,ty,flag = 0;
    //對這個點的上下左右都判斷，如果這個點周圍存在海洋，那麼就標記爲1
    for(i = 0;i < 4;i++)
    {
        tx = x + next[i][0];
        ty = y + next[i][1];
        if(tx < 0 || tx >= n || ty < 0 || ty >= n)
            continue;
        //如果這個點周圍存在沒有被淹沒的陸地，那麼就標記爲3
        if(book[tx][ty] == 2 || book[tx][ty] == 3)
            flag = 1;
        if(m[tx][ty] == '.')
        {
            book[x][y] = 1;
            return;
        }
    }
    if(flag)
        book[x][y] = 3;
    else
        book[x][y] = 2;
}

void dfs(int x, int y)
{
    int i,tx,ty;
    check(x, y);
    for(i = 0;i < 4;i++)
    {
        tx = x + next[i][0];
        ty = y + next[i][1];
        if(tx < 0 || tx >= n || ty < 0 || ty >= n)
            continue;
        //搜尋下一個沒有搜尋到的點
        if(!book[tx][ty] && m[tx][ty] == '#')
            dfs(tx,ty);
    }
    return;
}

int main()
{
    int i,j;
    scanf("%d",&n);
    sum = 0;
    for(i = 0;i < n;i++)
        scanf("%s",m[i]);
    for(i = 0;i < n;i++)
    {
        for(j = 0;j < n;j++)
        {
            if(m[i][j] == '#')
            {
                if(book[i][j] != 0)
                    continue;
                dfs(i,j);
                sum++;
            }
        }
    }
    for(i = 0;i < n;i++)
    {
        for(j = 0;j < n;j++)
        {
            if(book[i][j] == 2 && m[i][j] == '#')
                sum--;
        }
    }
    printf("%d\n",sum);
    return 0;
}

10.乘積最大

給定N個整數A1, A2, ... AN。請你從中選出K個數，使其乘積最大。  
請你求出最大的乘積，由於乘積可能超出整型範圍，你只需輸出乘積除以1000000009的餘數。

注意，如果X<0， 我們定義X除以1000000009的餘數是負(-X)除以1000000009的餘數。
即：0-( (0-x) % 1000000009)

【輸入格式】

第一行包含兩個整數N和K。  
以下N行每行一個整數Ai。

對於40%的數據，1 <= K <= N <= 100
對於60%的數據，1 <= K <= 1000
對於100%的數據，1 <= K <= N <= 100000 -100000 <= Ai <= 100000

【輸出格式】

一個整數，表示答案。

【輸入樣例】

【輸出樣例】

999100009

再例如：
【輸入樣例】

【輸出樣例】

-999999829

資源約定：

峯值記憶體消耗（含虛擬機器） < 256M
CPU消耗  < 1000ms

請嚴格按要求輸出，不要畫蛇添足地列印類似：「請您輸入…」的多餘內容。

注意：

main函數需要返回0;
只使用ANSI C/ANSI C++ 標準;
不要呼叫依賴於編譯環境或操作系統的特殊函數。
所有依賴的函數必須明確地在原始檔中 #include <xxx>
不能通過工程設定而省略常用標頭檔案。

提交程式時，注意選擇所期望的語言型別和編譯器型別。

10.1思路

感覺難點在分類討論的時候要把所有情況都考慮全，首先把這些數按照絕對值從大到小排序：

①當n==k時，只能全選了

②如果n個數全是正數，選擇前k個即可

③如果n個數全是負數，如果k是偶數，選擇前k個即可；如果k是奇數，選擇後k個即可

④剩下的情況就是有正有負了，先看前k個數，如果負數個數爲偶數，選擇前k個即可；如果負數個數爲奇數，則比較前面最後一個負數與後面第一個負數的乘積和前面最後一個正數與後面第一個正數的乘積哪個大，取大的即可

10.2原始碼

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<string>
#include<vector>
#include<queue>
#include<map>
#include<set>
using namespace std;
 
#define N 100000
#define MOD 1000000009
 
struct number
{
	int sign;
	long long num;
}a[N];
 
bool cmp(const number &x,const number &y)
{
	return x.num>y.num;
}
 
int main()
{
	int n,k,cnt=0;
	long long t,ans=1;
	cin>>n>>k;
	for(int i=0;i<n;i++)
	{
		cin>>t;
		if(t<0)
		{
			a[i].sign=-1;
			a[i].num=-t;
			cnt++;
		}
		else
		{
			a[i].sign=1;
			a[i].num=t;
		}
	}
	if(n==k)
	{
		for(int i=0;i<k;i++)
			ans=(ans*a[i].num)%MOD;
		if(cnt&1)
			ans=-ans;
	}
	else
	{
		sort(a,a+n,cmp);
		if(cnt==n)//全是負數 
		{
			if(k&1)
			{
				for(int i=n-1;i>n-1-k;i--)
					ans=(ans*a[i].num)%MOD;
				ans=-ans;
			}
			else
			{
				for(int i=0;i<k;i++)
					ans=(ans*a[i].num)%MOD;
			}
		}
		else if(cnt==0)//全是正數 
		{
			for(int i=0;i<k;i++)
				ans=(ans*a[i].num)%MOD;			
		}
		else
		{
			int nega=-1,posi=-1;
			cnt=0;
			for(int i=0;i<k;i++)
			{
				if(a[i].sign==-1) 
				{
					//nega記錄前K箇中最後一個負數的下標
					//cnt記錄前k箇中負數的個數，每滿2個就乘一次 
					cnt++;
					if(nega==-1)
						nega=i;
					else
					{						
						if((cnt&1)==0)//保持負數是一對的樣子乘上去 
						{
							ans=(ans*a[nega].num)%MOD;
							ans=(ans*a[i].num)%MOD;
						}
						nega=i;
					}
				}
				else
				{
					//posi記錄前k箇中最後一個正數的下標
					//每次只乘上前一個正數，留最後一個正數作交換 
					if(posi==-1)
						posi=i;
					else
					{
						ans=(ans*a[posi].num)%MOD;
						posi=i;
					}
				}
			}
			if((cnt&1)==0)//負數爲偶數個，則直接取前k個數即可，把最後一個正數乘上即可 
				ans=(ans*a[posi].num)%MOD;
			else
			{
				int nega1=-1,posi1=-1;
				for(int i=k;i<n;i++)
				{
					if(a[i].sign==-1)//找絕對值最大的負數 
					{
						if(nega1==-1)
							nega1=i;
					}
					else//找最大的正數 
					{
						if(posi1==-1)
							posi1=i;
					}
					if(nega1!=-1&&posi1!=-1)
						break;
				}
				if(nega1!=-1&&posi1!=-1)
				{
					//比較是前k箇中最後一個負數和後面絕對值最大的負數乘積大
					//還是前k箇中最後一個正數和後面最大的正數乘積大 
					if(a[nega].num*a[nega1].num>a[posi].num*a[posi1].num)
					{
						ans=(ans*a[nega].num)%MOD;
						ans=(ans*a[nega1].num)%MOD;
					}
					else
					{
						ans=(ans*a[posi].num)%MOD;
						ans=(ans*a[posi1].num)%MOD;						
					}
				}
				else if(posi1!=-1)//後面只有正數了 
				{
					ans=(ans*a[posi].num)%MOD;
					ans=(ans*a[posi1].num)%MOD;	
				}
				else//後面只有負數了 
				{
					ans=(ans*a[nega].num)%MOD;
					ans=(ans*a[nega1].num)%MOD;
				} 
			}
		}
	}
	cout<<ans<<endl;	
	return 0;
}

藍橋杯18年省賽真題

18年省賽真題筆記

1.第幾天

1.1思路

1.2原始碼

2.明碼

2.1思路

2.2 二進制求法

2.3原始碼

3.乘積尾零

3.1思路

3.2原始碼

4.測試次數

4.1思路

4.2原始碼

5.快速排序

5.1思路

5.2答案

6.遞增三元組

6.1思路

6.2原始碼

7.螺旋折線

7.1思路

7.2原始碼

8.日誌統計

8.1思路

8.2原始碼

9.全球變暖

9.1思路

9.2原始碼

10.乘積最大

10.1思路

10.2原始碼