數據結構與演算法（Python）

Why？

我們舉一個可能不太恰當的例子：

如果將最終寫好執行的程式比作戰場，我們碼農便是指揮作戰的將軍，而我們所寫的程式碼便是士兵和武器。

那麼數據結構和演算法是什麼？答曰：兵法！

我們可以不看兵法在戰場上肉搏，如此，可能會勝利，可能會失敗。即使勝利，可能也會付出巨大的代價。我們寫程式亦然：沒有看過數據結構和演算法，有時面對問題可能會沒有任何思路，不知如何下手去解決；大部分時間可能解決了問題，可是對程式執行的效率和開銷沒有意識，效能低下；有時會藉助別人開發的利器暫時解決了問題，可是遇到效能瓶頸的時候，又不知該如何進行鍼對性的優化。

如果我們常看兵法，便可做到胸有成竹，有時會事半功倍！同樣，如果我們常看數據結構與演算法，我們寫程式時也能遊刃有餘、明察秋毫，遇到問題時亦能入木三分、迎刃而解。

故，數據結構和演算法是一名程式開發人員的必備基本功，不是一朝一夕就能練成絕世高手的。冰凍三尺非一日之寒，需要我們平時不斷的主動去學習積累。

引入

先來看一道題:

如果 a+b+c=1000，且 a^2+b^2=c^2（a,b,c 爲自然數），如何求出所有a、b、c可能的組合?

第一次嘗試

import time

start_time = time.time()

for a in range(0,1001):
    for b in range(0,1001):
        for c in range(0,1001):
            if a**2 + b**2 == c**2 and a+b+c==1000:
                print("a,b,c:%d,%d,%d"%(a,b,c))

end_time = time.time()
print("elapsed:%F"%(end_time - start_time))
print("complete!")

執行結果：

a,b,c:0,500,500
a,b,c:200,375,425
a,b,c:375,200,425
a,b,c:500,0,500
elapsed:1072.429258
complete!

演算法的提出

演算法的概念

演算法是計算機處理資訊的本質，因爲計算機程式本質上是一個演算法來告訴計算機確切的步驟來執行一個指定的任務。一般地，當演算法在處理資訊時，會從輸入裝置或數據的儲存地址讀取數據，把結果寫入輸出裝置或某個儲存地址供以後再呼叫。

演算法是獨立存在的一種解決問題的方法和思想。

對於演算法而言，實現的語言並不重要，重要的是思想。

演算法可以有不同的語言描述實現版本（如C描述、C++描述、Python描述等），我們現在是在用Python語言進行描述實現。

演算法的五大特性

輸入: 演算法具有0個或多個輸入
輸出: 演算法至少有1個或多個輸出
有窮性: 演算法在有限的步驟之後會自動結束而不會無限回圈，並且每一個步驟可以在可接受的時間內完成
確定性：演算法中的每一步都有確定的含義，不會出現二義性
可行性：演算法的每一步都是可行的，也就是說每一步都能夠執行有限的次數完成

第二次嘗試

執行過程

import time

start_time = time.time()
for a in range(0,1001):
    for b in range(0,1001-a):
        c=1000-a-b
        if a**2 +b**2 == c**2:
            print("a,b,c:%d,%d,%d"%(a,b,c))

end_time=time.time()
print("elapsed:%f"%(end_time-start_time))
print("complete!")

輸出結果：

a,b,c:0,500,500
a,b,c:200,375,425
a,b,c:375,200,425
a,b,c:500,0,500
elapsed:0.551522
complete!

演算法效率衡量

執行時間反應演算法效率

對於同一問題，我們給出了兩種解決演算法，在兩種演算法的實現中，我們對程式執行的時間進行了測算，發現兩段程式執行的時間相差懸殊（214.583347秒相比於0.182897秒），由此我們可以得出結論：實現演算法程式的執行時間可以反應出演算法的效率，即演算法的優劣。

單靠時間值絕對可信嗎？

假設我們將第二次嘗試的演算法程式執行在一臺設定古老效能低下的計算機中，情況會如何？很可能執行的時間並不會比在我們的電腦中執行演算法一的214.583347秒快多少。

單純依靠執行的時間來比較演算法的優劣並不一定是客觀準確的！

程式的執行離不開計算機環境（包括硬體和操作系統），這些客觀原因會影響程式執行的速度並反應在程式的執行時間上。那麼如何才能纔能客觀的評判一個演算法的優劣呢？

時間複雜度與「大O記法」

我們假定計算機執行演算法每一個基本操作的時間是固定的一個時間單位，那麼有多少個基本操作就代表會花費多少時間單位。算然對於不同的機器環境而言，確切的單位時間是不同的，但是對於演算法進行多少個基本操作（即花費多少時間單位）在規模數量級上卻是相同的，由此可以忽略機器環境的影響而客觀的反應演算法的時間效率。

對於演算法的時間效率，我們可以用「大O記法」來表示。

「大O記法」：對於單調的整數函數f，如果存在一個整數函數g和實常數c>0，使得對於充分大的n總有f(n)<=c*g(n)，就說函數g是f的一個漸近函數（忽略常數），記爲f(n)=O(g(n))。也就是說，在趨向無窮的極限意義下，函數f的增長速度受到函數g的約束，亦即函數f與函數g的特徵相似。

時間複雜度：假設存在函數g，使得演算法A處理規模爲n的問題範例所用時間爲T(n)=O(g(n))，則稱O(g(n))爲演算法A的漸近時間複雜度，簡稱時間複雜度，記爲T(n)

如何理解「大O記法」

對於演算法進行特別具體的細緻分析雖然很好，但在實踐中的實際價值有限。對於演算法的時間性質和空間性質，最重要的是其數量級和趨勢，這些是分析演算法效率的主要部分。而計量演算法基本運算元量的規模函數中那些常數因子可以忽略不計。例如，可以認爲3n2和100n2屬於同一個量級，如果兩個演算法處理同樣規模範例的代價分別爲這兩個函數，就認爲它們的效率「差不多」，都爲n2級。

最壞時間複雜度

分析演算法時，存在幾種可能的考慮：

演算法完成工作最少需要多少基本操作，即最優時間複雜度
演算法完成工作最多需要多少基本操作，即最壞時間複雜度
演算法完成工作平均需要多少基本操作，即平均時間複雜度

對於最優時間複雜度，其價值不大，因爲它沒有提供什麼有用資訊，其反映的只是最樂觀最理想的情況，沒有參考價值。

對於最壞時間複雜度，提供了一種保證，表明演算法在此種程度的基本操作中一定能完成工作。

對於平均時間複雜度，是對演算法的一個全面評價，因此它完整全面的反映了這個演算法的性質。但另一方面，這種衡量並沒有保證，不是每個計算都能在這個基本操作內完成。而且，對於平均情況的計算，也會因爲應用演算法的範例分佈可能並不均勻而難以計算。

因此，我們主要關注演算法的最壞情況，亦即最壞時間複雜度。

時間複雜度的幾條基本計算規則

基本操作，即只有常數項，認爲其時間複雜度爲O(1)
順序結構，時間複雜度按加法進行計算
回圈結構，時間複雜度按乘法進行計算
分支結構，時間複雜度取最大值
判斷一個演算法的效率時，往往只需要關注運算元量的最高次項，其它次要項和常數項可以忽略
在沒有特殊說明時，我們所分析的演算法的時間複雜度都是指最壞時間複雜度

演算法分析

第一次嘗試的演算法核心部分

for a in range(0, 1001):
    for b in range(0, 1001):
        for c in range(0, 1001):
            if a**2 + b**2 == c**2 and a+b+c == 1000:
                print("a, b, c: %d, %d, %d" % (a, b, c))

時間複雜度：

T(n) = O(n*n*n) = O(n3)

第二次嘗試的演算法核心部分

for a in range(0, 1001):
    for b in range(0, 1001-a):
        c = 1000 - a - b
        if a**2 + b**2 == c**2:
            print("a, b, c: %d, %d, %d" % (a, b, c))

時間複雜度：

T(n) = O(n*n*(1+1)) = O(n*n) = O(n2)

由此可見，我們嘗試的第二種演算法要比第一種演算法的時間複雜度好多的。

常見時間複雜度

執行次數函數舉例	階	非正式術語
12	O(1)	常數階
2n+3	O(n)	線性階
3n2+2n+1	O(n2)	平方階
5log2n+20	O(logn)	對數階
2n+3nlog2n+19	O(nlogn)	nlogn階
6n3+2n2+3n+4	O(n3)	立方階
2n	O(2n)	指數階

注意，經常將log2n（以2爲底的對數）簡寫成logn

常見時間複雜度之間的關係

所消耗的時間從小到大

O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)

練習： 時間複雜度練習( 參考演算法的效率規則判斷 )
O(5)
O(2n + 1)
O(n²+ n + 1)
O(3n³+1)

Python內建型別效能分析

timeit模組

timeit模組可以用來測試一小段Python程式碼的執行速度。

class timeit.Timer(stmt='pass', setup='pass', timer=<timer function>)

Timer是測量小段程式碼執行速度的類。

stmt參數是要測試的程式碼語句（statment）；

setup參數是執行程式碼時需要的設定；

timer參數是一個定時器函數，與平臺有關。

timeit.Timer.timeit(number=1000000)

Timer類中測試語句執行速度的物件方法。number參數是測試程式碼時的測試次數，預設爲1000000次。方法返回執行程式碼的平均耗時，一個float型別的秒數。

list的操作測試

def test1():
    l=[]
    for i in range(1000):
        l=l+[i]
def test2():
    l=[]
    for i in range(1000):
        l.append(i)
def test3():
    l=[i for i in range(1000)]
def test4():
    l=list(range(1000))

from timeit import Timer

t1 = Timer("test1()", "from __main__ import test1")
print("concat",t1.timeit(number=1000),"seconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append",t2.timeit(number=1000),"seconds")
t3=Timer("test3()", "from __main__ import test3")
print("comprehension",t3.timeit(number=1000),"seconds")
t4=Timer("test4()", "from __main__ import test4")
print("list range",t4.timeit(number=1000),"seconds")

輸出結果：

concat 1.4801318 seconds
append 0.10420639999999981 seconds
comprehension 0.0391007000000001 seconds
list range 0.017839500000000008 seconds

pop操作測試

x = range(2000000)
pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "seconds")
x = range(2000000)
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "seconds")

# ('pop_zero ', 1.9101738929748535, 'seconds')
# ('pop_end ', 0.00023603439331054688, 'seconds')

測試pop操作：從結果可以看出，pop最後一個元素的效率遠遠高於pop第一個元素

可以自行嘗試下list的append(value)和insert(0,value),即一個後面插入和一個前面插入？？？

list內建操作的時間複雜度

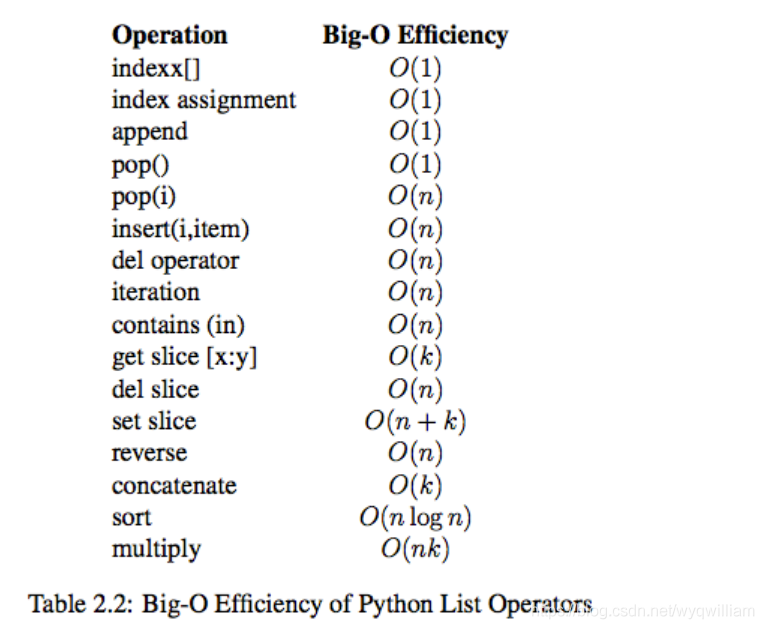
dict內建操作的時間複雜度

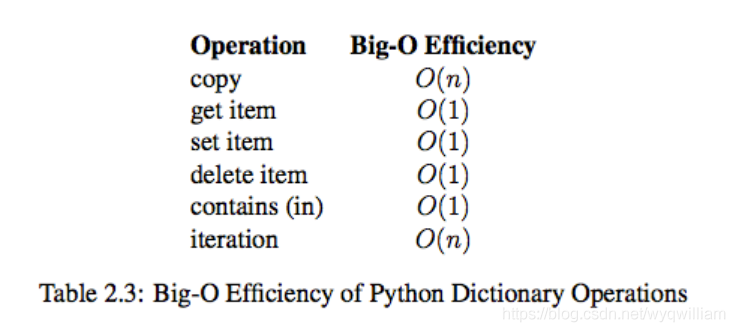
數據結構

我們如何用Python中的型別來儲存一個班的學生資訊？如果想要快速的通過學生姓名獲取其資訊呢？

實際上當我們在思考這個問題的時候，我們已經用到了數據結構。列表和字典都可以儲存一個班的學生資訊，但是想要在列表中獲取一名同學的資訊時，就要遍歷這個列表，其時間複雜度爲O(n)，而使用字典儲存時，可將學生姓名作爲字典的鍵，學生資訊作爲值，進而查詢時不需要遍歷便可快速獲取到學生資訊，其時間複雜度爲O(1)。

我們爲了解決問題，需要將數據儲存下來，然後根據數據的儲存方式來設計演算法實現進行處理，那麼數據的儲存方式不同就會導致需要不同的演算法進行處理。我們希望演算法解決問題的效率越快越好，於是我們就需要考慮數據究竟如何儲存的問題，這就是數據結構。

在上面的問題中我們可以選擇Python中的列表或字典來儲存學生資訊。列表和字典就是Python內建幫我們封裝好的兩種數據結構。

概念

數據是一個抽象的概念，將其進行分類後得到程式設計語言中的基本型別。如：int，float，char等。數據元素之間不是獨立的，存在特定的關係，這些關係便是結構。數據結構指數據物件中數據元素之間的關係。

Python給我們提供了很多現成的數據結構型別，這些系統自己定義好的，不需要我們自己去定義的數據結構叫做Python的內建數據結構，比如列表、元組、字典。而有些數據組織方式，Python系統裏面沒有直接定義，需要我們自己去定義實現這些數據的組織方式，這些數據組織方式稱之爲Python的擴充套件數據結構，比如棧，佇列等。

演算法與數據結構的區別

數據結構只是靜態的描述了數據元素之間的關係。

高效的程式需要在數據結構的基礎上設計和選擇演算法。

程式 = 數據結構 + 演算法

總結：演算法是爲了解決實際問題而設計的，數據結構是演算法需要處理的問題載體

抽象數據型別(Abstract Data Type)

抽象數據型別(ADT)的含義是指一個數學模型以及定義在此數學模型上的一組操作。即把數據型別和數據型別上的運算捆在一起，進行封裝。引入抽象數據型別的目的是把數據型別的表示和數據型別上運算的實現與這些數據型別和運算在程式中的參照隔開，使它們相互獨立。

最常用的數據運算有五種：

插入
刪除
修改
查詢
排序

數據結構與演算法的引入概念