順序表：棧 - tw511教學網

棧

棧的抽象數據型別及其實現

棧是一種特殊的線性表。在邏輯結構與儲存結構上，棧與一般的線性表沒有區別，但對允許的操作卻加以限制，棧的插入和刪除操作只允許在表尾一端進行。
棧可以順序儲存，也可以連線儲存。順序儲存的棧稱爲順序棧，連線儲存的棧稱爲鏈棧。
棧的插入和刪除操作只能在表的尾端進行，每次刪除的均爲最後進棧的元素，故棧也稱爲後進先出表（LIFO）。
棧中插入，刪除的一段稱爲棧頂，另一端稱爲棧底。
棧底固定不動，棧頂隨着插入和刪除操作不斷變化。
不含棧元素的棧稱爲空棧。
爲了對棧中運算處理的方便，設定了一個棧頂指針top，伊總是指向最後一個進棧的棧元素。
棧頂指針實際上是陣列的下標，伊的正常取值範圍應是0~MaxSize-1。當top=-1時，表示棧爲空，不能再進行刪除操作；當top等於MaxSize-1時，表示棧已滿，再進行插入操作會溢位。

建構函式Stack(int s)

//類操作的實現
template<class T>
Stack<T>::Stack(int s)
{
    //建構函式：建立棧空間，生成一個空棧
    MaxSize=s;
    elements=new T[MaxSize];  //建立棧空間
    top=-1;       //生成一個空棧 
}

進棧Push(const T& item)

template<class T>
Stack<T>::Push(const T& item)
{
    //進棧：若棧不滿，則item進棧，返回0，否則返回-1 
    if(!IsFull())      
    {
  	elements[++top]=item;
  	return 0;
    }
    else
    {
  	return -1;
    }
}

出棧Pop(void)

template<class T>
Stack<T>::Pop(void)
{
    //出棧：若棧非空，則棧頂元素出棧，返回其值，否則返回NULL 
    if(!IsEmpty())      
    {
  	return elements[top--];
    }
    else
    {
  	return NULL;
    }
}

讀棧頂元素

template<class T>
Stack<T>::GetTop(void)
{
    //讀棧頂：若棧非空，則返回棧頂元素的值，否則返回NULL 
    if(!IsEmpty())      
    {
  	return elements[top];
    }
    else
    {
  	return NULL;
    }
}

棧的應用

表達式的記值

此處只考慮常數表達式的情況，假設：表達式中的運算元只允許爲個位的整形常數（若爲多位數，可用"."分隔兩運算元）；除整形常數外，只含有二元運算子（+，-，*，、）和括號（（，））；記值順序遵循四則運演算法則，表達式無語法錯誤。
譯程式掃描表達式(表達式在源程式中是以字串的形式表示的)，析取一個「單詞」 ——運算元或運算子,是運算元則進運算元棧，是運算子則進運算子棧，但運算子在進棧時要按運演算法則作如下處理:

(1)當運算子棧爲空時，析取的運算子無條件進棧。
當運算子棧頂爲「*」或「/」時，若析取的運算子爲「(」，則進棧;否則，先執行出棧操作，並執行(6)的操作，然後該運算子再進棧。
當運算子棧頂爲「+」或「-」時,若析取的運算子爲「(」、「*」或「/」，則進棧;否則，先執行出棧操作，並執行(6)的操作，然後該運算子再進棧。
當運算子棧頂爲「(」時，析取的運算子除「)」之外都可進棧。
若析取的運算子爲「)」，則先要連續執行出棧操作，直到出棧的運算子爲「(」時爲止,實際上，「)」並不進棧。
除了「(」之外，每當一個運算子出棧時，要將運算元棧的棧頂和次棧頂出棧，進行該運算子所規定的運算,運算結果立即又進運算元棧。「("出棧時,運算元棧不做任何操作。
當表達式掃描結束後,若運算子棧還有運算子，則將運算子一一出棧,並執行(6)的操作。當運算子棧爲空時，運算元棧的棧頂內容就是整個表達式的值。
例如，表達式2* (3+4)- 8/2的計值過程如圖所示。

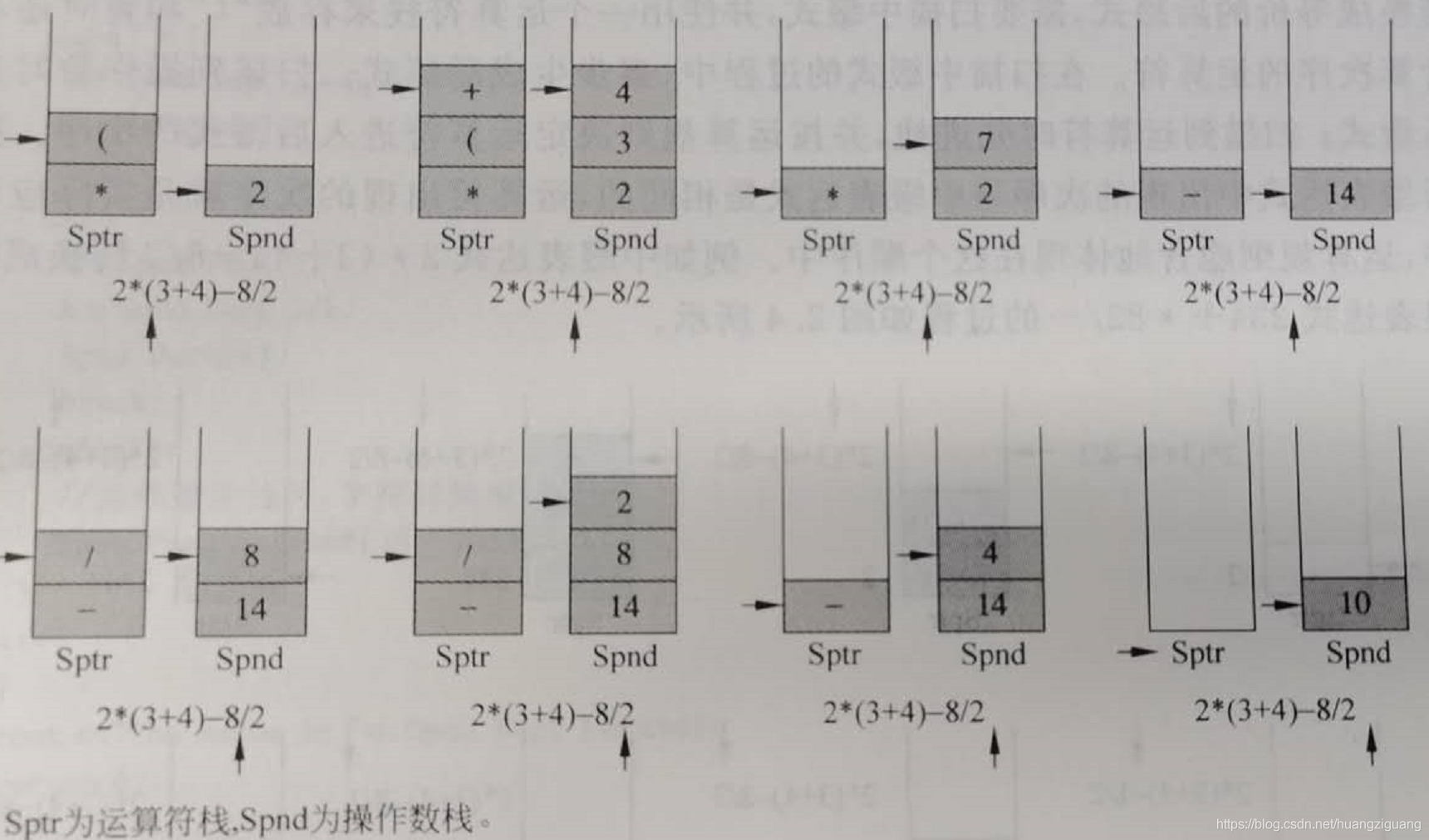
在實際的表達式計值中往往採用另一種處理方法，即先把中綴式轉換成後綴式，然後對後綴式進行計值處理。把運算元所執行運算的運算子放在運算元之後的表示方式稱爲後綴式。例如，中綴表達式2* (3+4)-8/2對應的後綴式爲234+ *82/-.
一個表達式的中綴式和對應的後綴式是等價的，即表達式的計算順序和結果完全相同。但在後綴式中沒有了括號,運算子緊跟在兩個運算元後面，所有的計算按運算子出現的順序，嚴格從左向右進行，而不必考慮運算子的優先規則。後綴式的計值只需一個運算元棧。
編譯程式在掃描後綴表達式時，若析取一個運算元，則立即進棧;若析取一個運算子，則將運算元棧的棧頂和次棧頂連續出棧,使出棧的兩個運算元執行運算子規定的運算,並將運算結果進棧。後綴表達式掃描結束時，運算元棧的棧頂內容即爲表達式的值。例如後綴表達式234+*82/-的計值過程如圖所示。
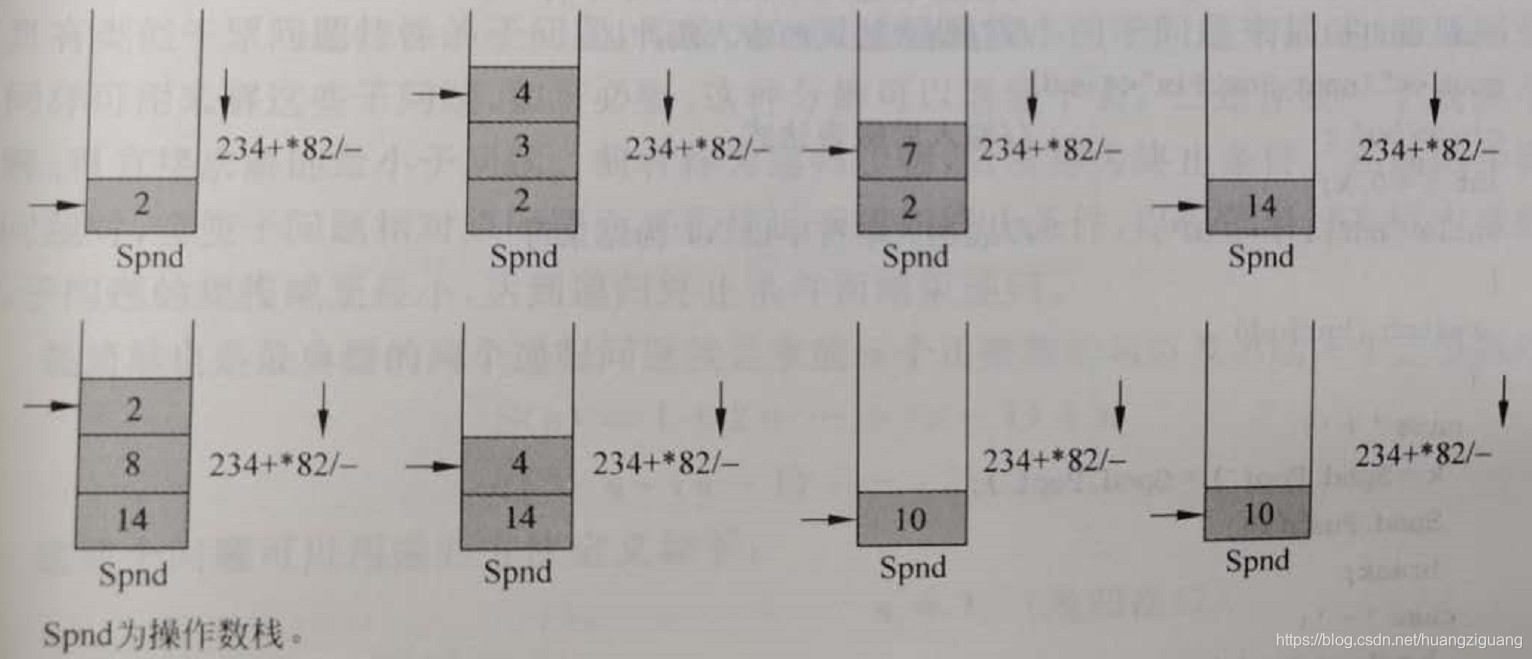
在这里插入图片描述
後綴表達式的計值只需一個棧，而且不必考慮運算子的優先規則，顯然比中綴表達式的計值要簡單得多,但這種簡單性的優勢是以中綴式到後綴式的轉換爲代價的。爲了把中綴式轉換成等價的後綴式，需要掃描中綴式，並使用一個運算子棧來存放「(」和暫時還不能確
定計算次序的運算子。在掃描中綴式的過程中，逐步生成後綴式。掃描到運算元時直接進人後綴式;掃描到運算子時先進棧，並按運算規則決定運算子進人後綴式的次序。運算元在後綴表達式中出現的次序與中綴表達式是相同的，運算子出現的次序就是實際應計算的順序,運算規則隱含地體現在這個順序中。例如中綴表達式2*(3+4)-8/2轉換成等價的後綴表達式234+ * 82/-的過程如圖所示。
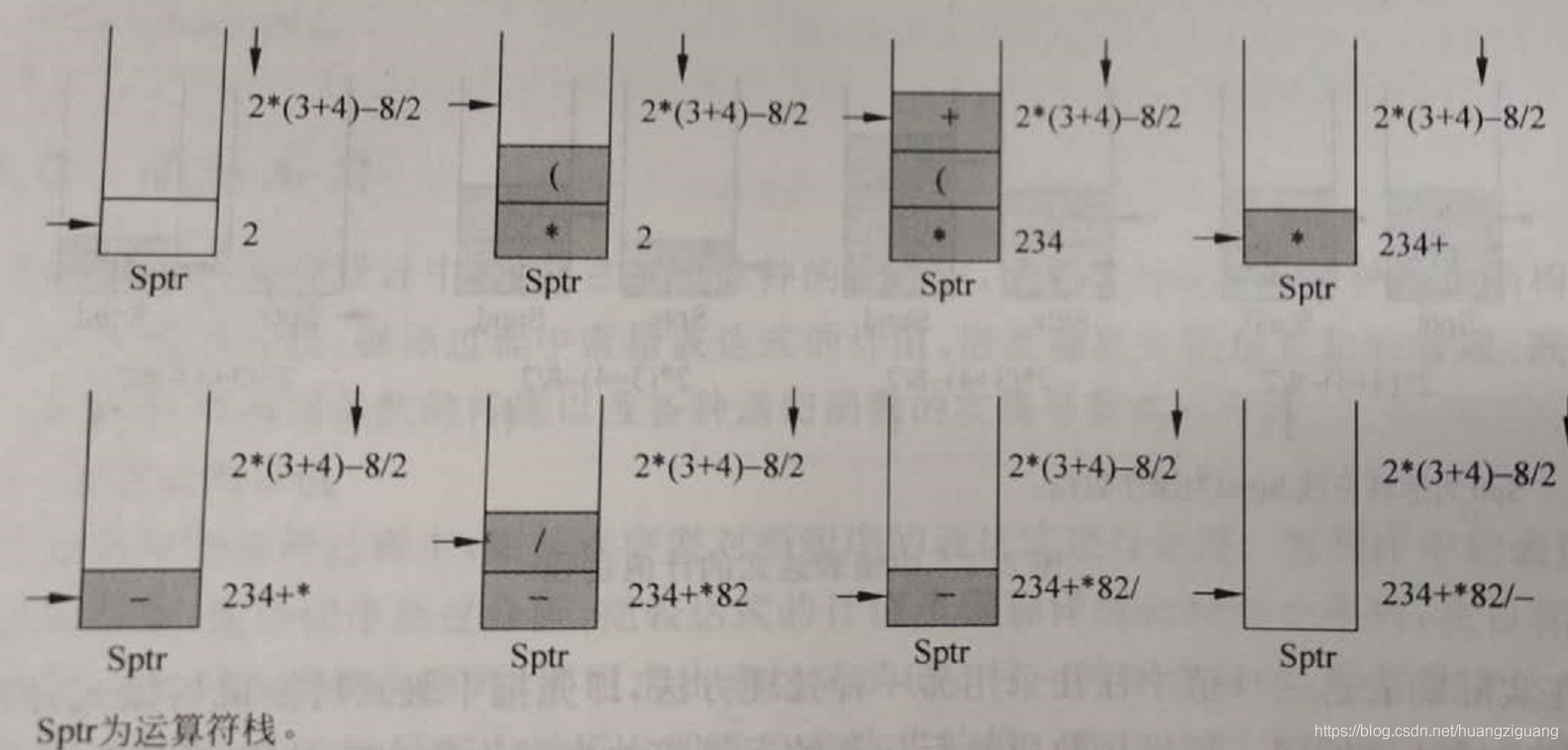
在这里插入图片描述

後綴表達式記值

int EvaluatePostfix(void)
{
 //後綴表達式的記值
 //假設運算子只有+，-，*，/，運算元都是個位數，後綴表達式無語法錯誤
 Stack<int>Spnd(80);
 const int size=80;   //限定表達式最長爲79個字元
 char buf[size];    //儲存表達式的輸入緩衝區
 cout<<"Input Postfix"<<endl;
 cin>>buf;     //輸入後綴表達式
 int i=0,k;
 while(buf[i]!='\0')
 {
  switch(buf[i])
  {
   case '+':
    k=Spnd.Pop()+Spnd.Pop();
    Spnd.Push(k);
    break;
   case '-':
    k=Spnd.Pop();
    k=Spnd.Pop()-k;
    Spnd.Push(k);
    break;
   case '+':
    k=Spnd.Pop()*Spnd.Pop();
    Spnd.Push(k);
    break;
   case '+':
    k=Spnd.Pop();
    k=Spnd.Pop()/k;
    Spnd.Push(k);
    break; 
   default:
    //運算元進棧時，字元轉換爲數值
    Spnd.Push(intbuf[i]-48); 
  }
  i++;
 }
 cout<<"The value is "<<Spnd.Pop()<<endl;
 return 0; 
}

棧與遞回

求前n個正整數的和的遞回演算法

int sum(int n)
{
    //設n是正整數
    if(n==1)
    {
        return 1;
    }
    else
    {
        return n+sum(n-1);
    }
}

求前n個正整數的積的遞回演算法

int factorial(int n)
{
    //設n是非負整數
    if(n==0)
    {
        return 1;
    }
    else
    {
        return n*factorial(n-1);
    }
}

漢諾塔問題的遞回演算法

void hanoi(int n,char a,char b,char c)
{
    //將n個盤子從a柱移到c柱
    //只有1個盤子，直接移動
    if(n==1)
    {
  	cout<<"move"<<a<<"to"<<c<<endl;
    }
    else
    {
  	//將n-1個盤子從a柱移到b柱
  	hanoi(n-1,a,c,b);
  	//最後1個盤子從a柱移到c柱
  	cout<<"move"<<a<<"to"<<c<<endl;
  	//將n-1個盤子從b柱移到c柱
  	hanoi(n-1,b,a,c);
    } 
}
int main()
{
    int n;//盤子個數
    char A='1',B='2',C='3';//柱名
    cout<<"Enter the numbers of disks:";
    cin>>n;
    cout<<"The solution for n="<<n<<endl;
    hanoi(n,A,B,C);  
}

小結：

遞回過程在計算機中實現時必須依賴堆疊
使用遞回前，需權衡設計和估計執行的複雜度，當強調演算法設計且在執行時有合理的空間複雜度和時間複雜度時，應使用遞回。