Matplotlib繪製高階影象

本節將講解的Matplotlib繪製高階影象主要包含兩種影象:

三維影象
地理影象

Matplotlib繪製三維影象直接使用自帶的mplot3d工具箱來繪製,Matplotlib繪製地理影象則要使用Basemap工具箱

由於Basemap工具箱不是自帶的,因此需要額外下載

Matplotlib繪製三維影象

Matplotlib原本只能繪製二維影象,但是隨着版本的迭代逐漸開始可以繪製三維影象了

繪製三維影象的工具箱是mplot3d,我們需要從mpl_toolkits匯入這個工具箱,實際上所有基於Matplotlib開發的高階功能庫都位於這個位置,並且也能夠被稱爲工具箱

我們首先需要匯入這個工具箱

from mpl_toolkits import mplot3d

指定projection參數建立三維子圖

和二維影象的情況一樣,三維影象也需要三維子圖承載,爲此,我們匯入mplot3d工具箱之後,在任何可以建立二維Axes物件的函數或者方法中指定projection參數爲3d後即可建立一個三維子圖(Axes3D物件)

from mpl_toolkits import mplot3d

Fig=plt.figure()
Axes3D=plt.axes(projection='3d')
print(type(Axes3D))
plt.show()
>>>
<class 'matplotlib.axes._subplots.Axes3DSubplot'>

在这里插入图片描述

這個網格圖可以用滑鼠來進行互動

Axes3D.plot3D()與Axes3D.scatter3D()繪製三維點與線

最基本的三維影象是(x,y,z)三維座標點構成的線圖與散點圖.我們分別可以使用Axes3D物件的plot3D()和scatter3D()方法來繪製

from mpl_toolkits import mplot3d

z=np.linspace(start=0,stop=15,num=1000)
x=np.sin(z)
y=np.cos(z)

z_scatter=15*np.random.random(100)
x_scatter=np.sin(z_scatter)+0.1*np.random.randn(100)
y_scatter=np.cos(z_scatter)+0.1*np.random.randn(100)

Fig=plt.figure()
Axes3D=plt.axes(projection='3d')
Axes3D.plot3D(x,y,z,'gray')
Axes3D.scatter3D(x_scatter,y_scatter,z_scatter,c=z_scatter,cmap='Greens')
plt.show()

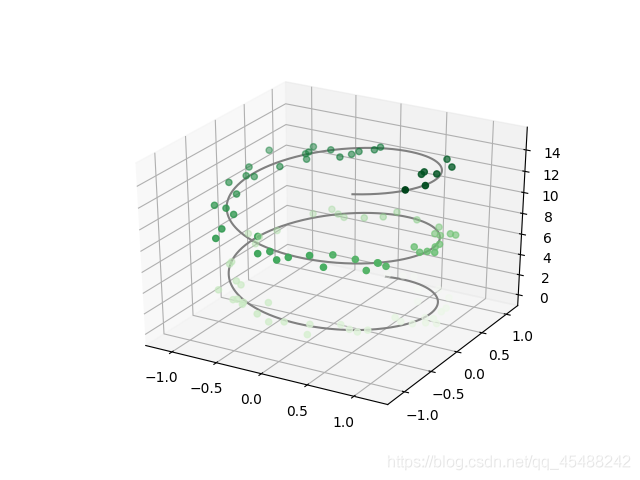
在这里插入图片描述

mplot3d自動的會將一些點設定爲透明的,來表現整個影象的立體感,我們通過互動拖拽影象就能夠得到透明的點的變化

Axes3D.contour3D()繪製三維等高線圖

前面介紹過將三維影象投影到二維影象上繪製等高線圖,我們其實可以通過mplot3d直接繪製三維等高線圖

和Axes.contour()方法一樣,Axes3D.contour3D()物件我們傳入的xoy面的數據必須是二維網格數據

x=np.linspace(start=-6,stop=6,num=30)
y=np.linspace(start=-6,stop=6,num=30)

x_grid,y_grid=np.meshgrid(x,y)
z_grid=np.sin(np.sqrt(x_grid**2+y_grid**2))

Fig=plt.figure()
Axes3D=plt.axes(projection='3d')

Axes3D.contour3D(x_grid,y_grid,z_grid,50,cmap='RdGy')
Axes3D.set_xlabel('x')
Axes3D.set_ylabel('y')
Axes3D.set_zlabel('z')

plt.show()

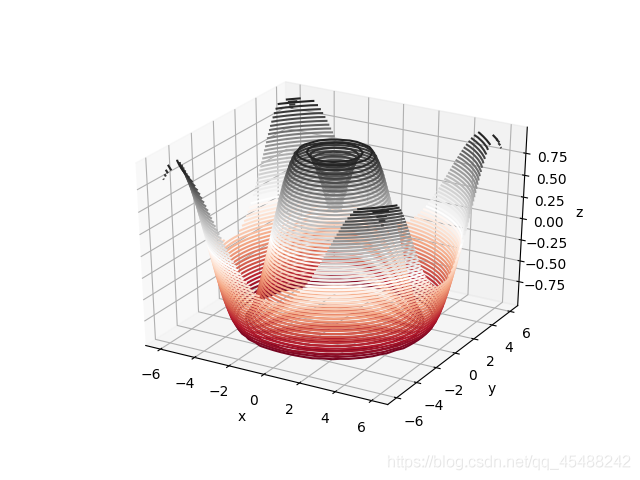
在这里插入图片描述

由於這個角度不是觀察的最佳視角

我們可以通過Axes3D.view_init()方法來調整視角

x=np.linspace(start=-6,stop=6,num=30)
y=np.linspace(start=-6,stop=6,num=30)

x_grid,y_grid=np.meshgrid(x,y)
z_grid=np.sin(np.sqrt(x_grid**2+y_grid**2))

Fig=plt.figure()
Axes3D=plt.axes(projection='3d')

Axes3D.contour3D(x_grid,y_grid,z_grid,50,cmap='RdGy')
Axes3D.set_xlabel('x')
Axes3D.set_ylabel('y')
Axes3D.set_zlabel('z')

Axes3D.view_init(60,35)				#調整俯視角爲60度,方位角是35度

plt.show()

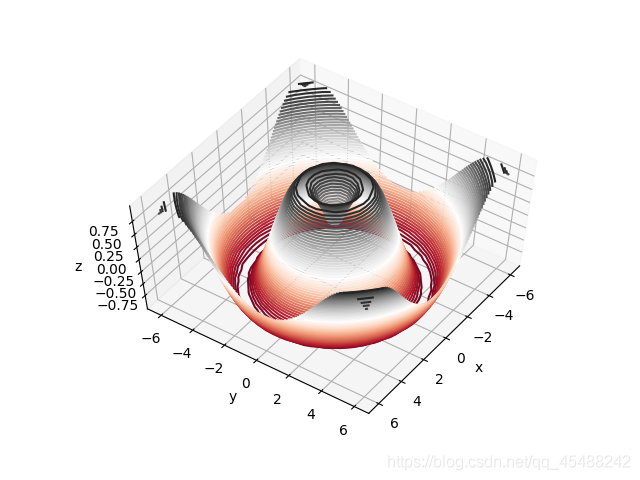
在这里插入图片描述

Axes3D.plot_wireframe()繪製線框圖

線框圖和下面下麪將要講解的曲面圖都是二維平面直接對映到三維空間中的曲面.我們可以使用plot_wireframe()

x=np.linspace(start=-6,stop=6,num=30)
y=np.linspace(start=-6,stop=6,num=30)

x_grid,y_grid=np.meshgrid(x,y)
z_grid=np.sin(np.sqrt(x_grid**2+y_grid**2))

Fig=plt.figure()
Axes3D=plt.axes(projection='3d')

Axes3D.plot_wireframe(x_grid,y_grid,z_grid,color='black')
Axes3D.set_title('wireframe')

plt.show()

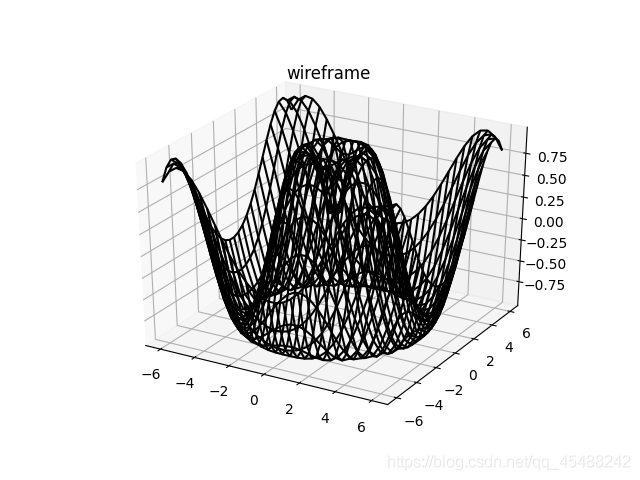
在这里插入图片描述

Axes3D.plot_surface()繪製曲面圖

和前面的繪製線框圖類似,我們爲plot_surface傳入三個網格數據即可繪製

x=np.linspace(start=-6,stop=6,num=30)
y=np.linspace(start=-6,stop=6,num=30)

x_grid,y_grid=np.meshgrid(x,y)
z_grid=np.sin(np.sqrt(x_grid**2+y_grid**2))

Fig=plt.figure()
Axes3D=plt.axes(projection='3d')

Axes3D.plot_surface(x_grid,y_grid,z_grid,rstride=1,cstride=1,cmap='viridis')
Axes3D.set_title('surface')

plt.show()

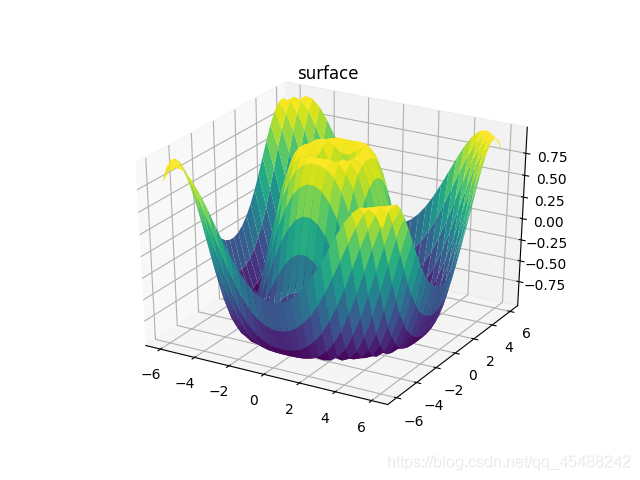
在这里插入图片描述

此外,我們實際上也可以使用柱座標來繪圖,此時只需要將x和y轉變爲r和theta

r=np.linspace(start=0,stop=6,num=20)
theta=np.linspace(start=0,stop=1.7*np.pi,num=50)

r_grid,theta_grid=np.meshgrid(r,theta)
x_grid=r_grid*np.sin(theta_grid)
y_grid=r_grid*np.cos(theta_grid)
z_grid=np.sin(np.sqrt(x_grid**2+y_grid**2))

Fig=plt.figure()
Axes3D=plt.axes(projection='3d')

Axes3D.plot_surface(x_grid,y_grid,z_grid,rstride=1,cstride=1,cmap='RdGy',edgecolor='none')
plt.show()

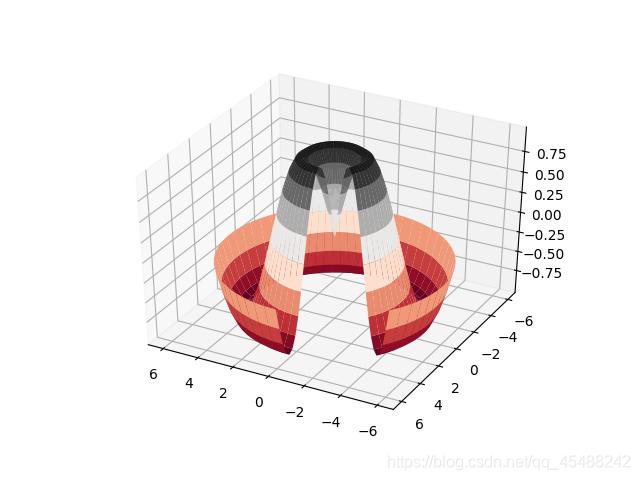
在这里插入图片描述

我們通過定義域的轉變的方式來實現了對曲面的剖分

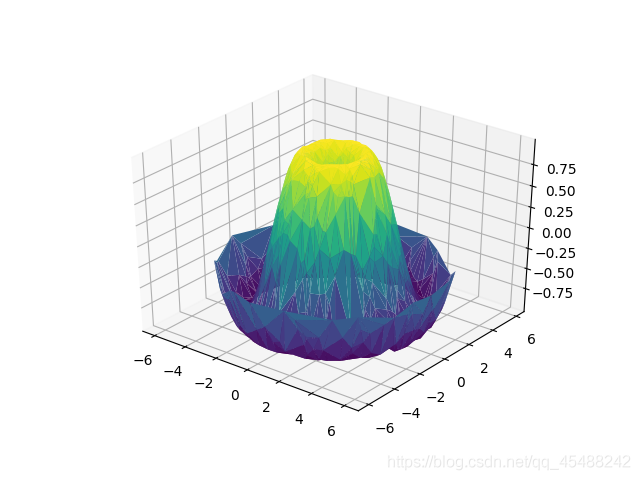
Axes3D.plot_trisurf()擬合曲面

上各種繪製曲面的方法,要麼需要笛卡爾座標,要麼使用極座標,並且需要對每個數據點生成網格,而後才能纔能後進行繪圖曲面

但在進行正常工作的時候,我們往往可能遇到的情況是由多個數據點而非嚴格的,均勻的網格數據

爲此,我們想要對這些數據點所在的曲面進行擬合,這就需要Axes3D物件的plot_trisurf()方法來繪製

我們首先建立一些隨機點,並觀察這些點的分佈來對數據的分佈具有一個大概的認識

# 隨機生成點
theta=2*np.pi*np.random.random(1000)
r=6*np.random.random(1000)
x=np.ravel(r*np.sin(theta))					#使用np.ravel來確保x是一維的陣列
y=np.ravel(r*np.cos(theta))					#同上,確保y是一維的陣列
z=np.sin(np.sqrt(x**2+y**2))

Fig=plt.figure()
Axes3D=plt.axes(projection='3d')

Axes3D.scatter3D(x,y,z)

plt.show()

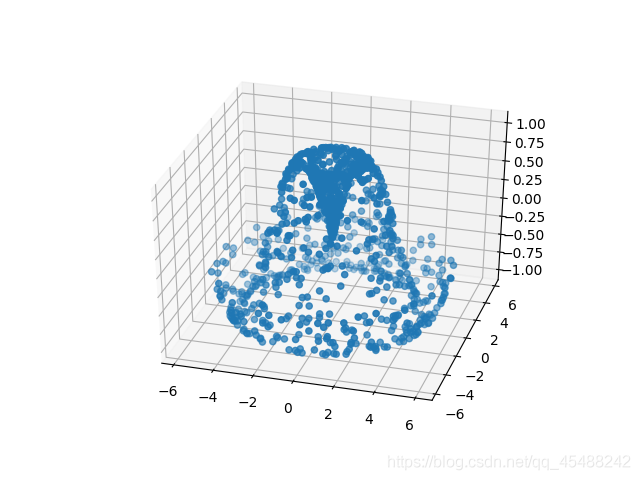
在这里插入图片描述

接下來我們呼叫plot_trisurf()來進行曲面擬合

# 隨機生成點
theta=2*np.pi*np.random.random(1000)
r=6*np.random.random(1000)
x=np.ravel(r*np.sin(theta))
y=np.ravel(r*np.cos(theta))
z=np.sin(np.sqrt(x**2+y**2))

Fig=plt.figure()
Axes3D=plt.axes(projection='3d')

Axes3D.plot_trisurf(x,y,z,cmap='viridis',edgecolor='none')

plt.show()

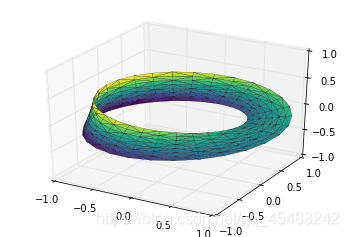
在这里插入图片描述

案例:莫比烏斯環

下面下麪我們將使用上面講解的內容來繪製一個莫比烏斯環

繪製莫比烏斯環的關鍵就是確定每個點的三個座標資訊.

莫比烏斯環的紙帶我們可以理解有兩種旋轉關係,一種是圍繞z軸進行旋轉,另外一種是圍繞自己的座標軸旋轉

藉此,我們可以確定莫比烏斯環上每個點的座標

r = 1 + w * np.cos(phi)

x = np.ravel(r * np.cos(theta))
y = np.ravel(r * np.sin(theta))
z = np.ravel(w * np.sin(phi))

from matplotlib.tri import Triangulation
tri = Triangulation(np.ravel(w), np.ravel(theta))

ax = plt.axes(projection='3d')
ax.plot_trisurf(x, y, z, triangles=tri.triangles,
                cmap='viridis', linewidths=0.2)

ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.set_zlim(-1, 1)

plt.show()

在这里插入图片描述

Matplotlib使用Basemap繪製地圖影象

Basemap是Matplotlib的一個第三方開發的工具箱.

Basemap用起來會比較笨重,但是對於Python使用者來來說還是很方便的

下面下麪我們首先需要安裝Basemap,然後在此基礎上進行繪製

安裝Basemap

Basemap實際不僅僅基於Matplotlib,還基於pyproj等地圖管理庫

因此想要正確的安裝並能執行Basemap,安裝的各個依賴庫的版本必須要對,否則就要用pip重灌

下面下麪首先指出各個依賴庫的版本

庫名	適用版本
six	1.15.0
matplotlib	2.2.0
geos	0.2.2
pyproj	1.9.6

注意.pyproj需要使用1.9.6,否則會報錯(我一開始使用的2.6.1的pyproj),matplotlib需要使用2.x版本,我一開始使用的是matplotlib3.x,這樣就會報錯

geos和basemap的安裝步驟參考csdn博文即可

Basemap的基礎概念

藍色彈珠

下面下麪我們將建立一個地球的藍色彈珠影象，來講解Basemap中的基礎概念

from mpl_toolkits.basemap import Basemap

Fig=plt.figure(figsize=(8,8))
m=Basemap(projection='ortho',resolution=None,lat_0=50,lon_0=-100)

m.bluemarble(scale=0.5)
print(type(m))

plt.show()
>>>
<class 'mpl_toolkits.basemap.Basemap'>

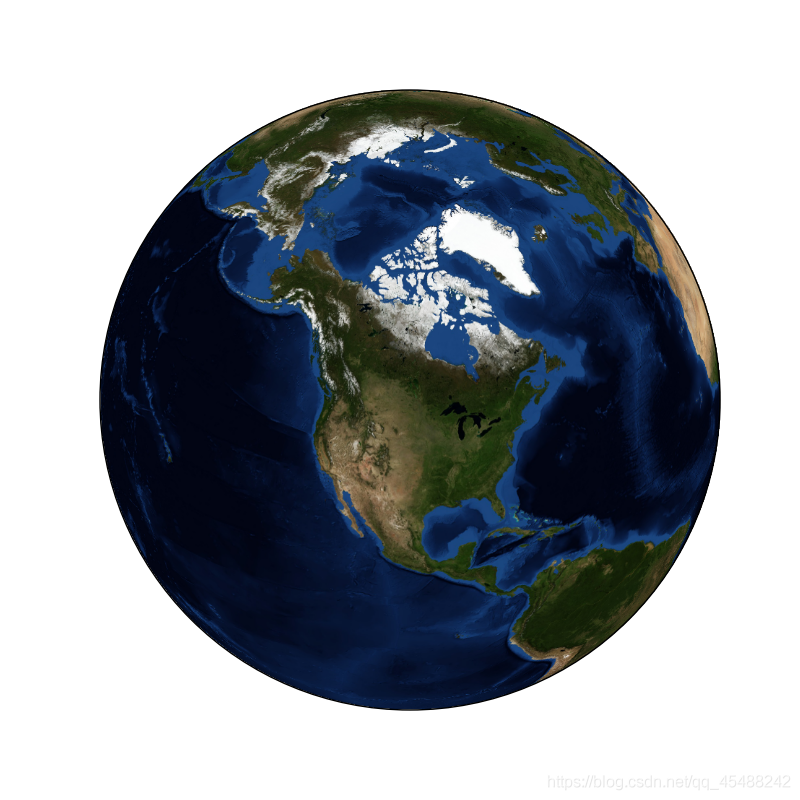
在这里插入图片描述

這裏我們首先從basemap庫中匯入了Basemap物件，Basemap物件是Basemap庫中的核心物件，就像Pandas中的Series和DataFrame物件，Numpy中的Ndarry物件一樣

Basemap庫內建了全球的地理數據，包括經度(Longitude)，緯度（Latitude)以及對應的影象，因此我們如果想要顯示某個地區的影象，那麼首先就需要指定顯示的地點的經緯度以及影象的範圍，所以我們範例化一個Basemap物件其實就是確定其地理數據範圍，注意Basemap僅僅作爲地理數據範圍，而非影象

顯示出具體的影象需要我們呼叫Basemap的不同方法來繪製圖像，例如我們這裏呼叫bluemarble方法來將這些數據視覺化

此外，由於地球是一個三維球體，因此其表面的地理影象自然分佈在球面上，所以這個時候就有一個至關重要的問題：如何將三維影象(地球上的地理影象)表現在二點陣圖像上

這個問題最早出現在繪圖領域，當時的人們面臨如何繪製地圖

解決這個問題的關鍵就是投影，我們可以通過各種不同的方式將三維球面投影到二維平面，從而使得二維影象能夠表示出地理影象

不同的投影方式的優點不同，因此在我們關注於不同的重點時，往往會選擇不同的投影方式來繪製地圖

因此，我們範例化一個Basemap物件的時候，不僅需要指定繪製地點的經度和緯度，還需要指定投影方式，至於圖形的大小，可以直接使用缺失值也可以指定

這裏我們首先建立了一個空白的Figure物件，接下來我們指定了投影的方式爲正射投影(ortho)，這樣便於我們從高空觀察地球整體的影象

接下來我們指定顯示的地點的經緯度爲-100和50

此外，Basemap物件還具有許多方法，這裏我們呼叫了bluemarble方法來繪製地球的藍色彈珠影象

球面座標

下面下麪我們將繪製西安的位置來進一步掌握Basemap的基礎概念

from mpl_toolkits.basemap import Basemap


Fig=plt.figure(figsize=(8,8))
m=Basemap(projection='lcc',resolution=None,\
    lat_0=33.8,lon_0=108.4,\
    width=8E6,height=8E6)

Longitude_XiAn,Latitude_XiAn=m(108.4,33.8)

m.etopo(scale=0.5,alpha=0.5)
plt.plot(Latitude_XiAn,Longitude_XiAn,'or',markersize=5)
plt.text(Latitude_XiAn+8E4,Longitude_XiAn+8E4,"Xi'an")

plt.show())

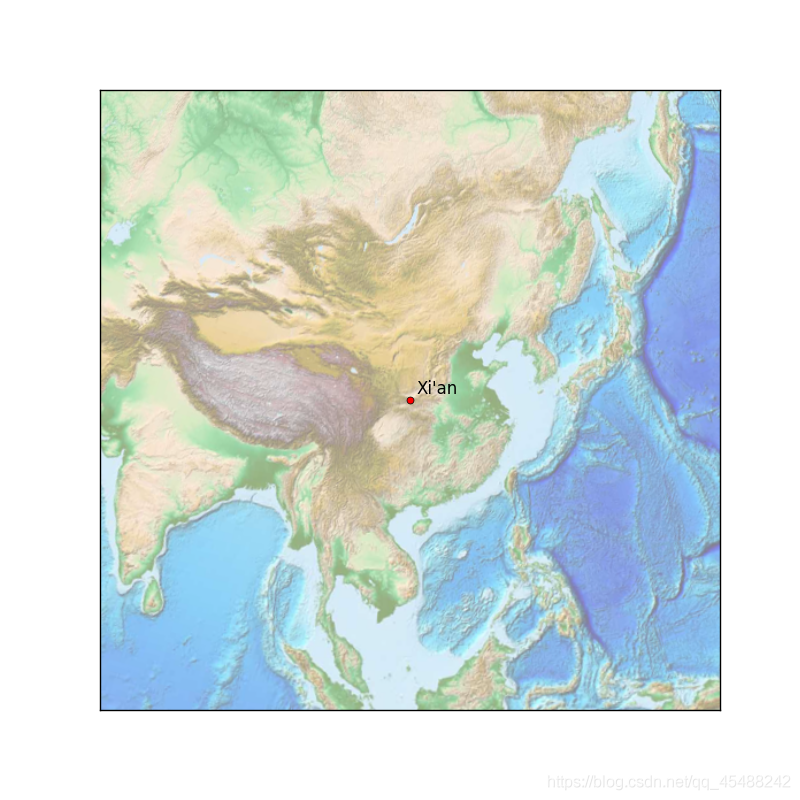
在这里插入图片描述

這裏我們首先範例化一個Basemap物件，確定其數據範圍爲以西安爲中心(其實就是程式碼中的經緯度)，投影方式爲蘭伯特等角圓錐投影(Lambert conforml conic projection, lcc),這種投影方式用來顯示區域性的地區效果會很好，具體將在後面講解

而實際上，我們通過各種方法視覺化的地理影象(這裏我們使用Etopo方法，這是一種能夠陸地與海底地形特徵的繪圖方式)其實是Matplotlib中的Axes物件下的一個子類AxesImage物件

但是作爲子類，AxesImage物件並不能像Axes物件一樣呼叫所有方法,例如Axes.plot()方法，所以我們不能夠使用AxesImage.plot()繪製散點圖來,進而新增西安這個點

因此實際上,我們呼叫Basemap的視覺化方法繪製的其實是背景,即地圖背景

還需要說明的是，Basemap視覺化得到的AxesImage物件是基於球面座標的，因此我們想要爲AxesImage物件新增點的時候，必須先要將點的經緯度轉換爲球面座標，這樣才能纔能夠正確的繪製，即程式碼中的Longitude_XiAn,Latitude_XiAn=m(108.4,33.8)語句

下面下麪我們來檢驗一下上面的內容

from mpl_toolkits.basemap import Basemap


Fig=plt.figure(figsize=(8,8))
m=Basemap(projection='lcc',resolution=None,\
    lat_0=33.8,lon_0=108.4,\
    width=8E6,height=8E6)

Longitude_XiAn,Latitude_XiAn=m(108.4,33.8)

AxesImage_XiAn=m.etopo(scale=0.5,alpha=0.5)
plt.plot(Latitude_XiAn,Longitude_XiAn,'or',markersize=5)
plt.text(Latitude_XiAn+8E4,Longitude_XiAn+8E4,"Xi'an")


print(type(AxesImage_XiAn))
print(type(Longitude_XiAn),Longitude_XiAn)
print(type(Latitude_XiAn),Latitude_XiAn)
>>>
<class 'matplotlib.image.AxesImage'>
<type 'float'>　 3999999.9999999986
<type 'float'>　 3999999.999999997

Basemap的投影方式

Basemap中具有三十多種投影方式,下面下麪我們將講解Basemap中的常見的投影方式

我們首先定義一個可以繪製經緯線的函數,在下面下麪每種投影風格的演示中,我們將使用這個函數來檢視效果\

def DrawMap(m,scale=0.2):

    from itertools import chain
    
    #繪製地貌暈染圖
    m.shadedrelief(scale=scale)

    #繪製經緯度
    Latitude=m.drawparallels(np.linspace(start=-90,stop=90,num=13))
    Longitude=m.drawmeridians(np.linspace(start=-180,stop=180,num=13))

    #生成經緯線數據以便於設定經緯線樣式
    LatitudeLines=chain(*(tup[1][0] for tup in Latitude.items()))
    LongitudeLines=chain(*(tup[1][0] for tup in Longitude.items()))
    AllLines=chain(LatitudeLines,LongitudeLines)

    #設定經緯線樣式
    for line in AllLines:
        line.set(linestyle='-',alpha=0.3,color='w')

    plt.show()

這裏我們首先匯入了itertools這個庫,itertool的主要用途就是進行高效的迭代,主要用於後面我們繪製經緯線時使用

我們呼叫了Basemap的shadedrelief方法來繪製地貌暈染圖.在前面講過,我們如果需要在Basemap繪製的地形圖上繪製點或線,那麼首先就需要將點和線(其實就是以點爲元素的列表)的直角座標轉換爲球座標.

這裏我們使用的Basemap物件的drawparallels和drawmeridian方法來繪製緯度線和經度線,注意,通過這兩種方法得到的返回值其實是一個字典,字典的鍵是plt.Line2D物件

接下來我們使用itertools庫的chain方法,chain方法是將多個物件串聯成一個新的可迭代物件的方法,這裏我們呼叫字典物件的items()方法將所有字典的鍵值對(元組形式)的鍵取出,傳給chain方法.但是由於取出的所有的鍵是一個不定長的陣列,因此要加上*

最後,通過chain方法生成的新的可迭代物件中的所有的元素都是plt.Line2D物件,包含所有的經緯線,我們迭代設定樣式即可

圓柱投影　Cylindrical Projection

圓柱投影是最簡單的地圖投影型別,我們將經度線和緯度線分別對映成水平線與豎直線,從而將球形地圖對映爲一個矩形影象

但是通過圓柱投影得到的地圖在赤道部分的表現會很好,但是在兩個極地部分的表現會因爲產生了畸變而很差

此外,根據經緯線的排布方式,我們還有等距圓柱投影(cyl),等積圓柱投影(cea,cylindrical equal-area),墨卡托圓柱投影(merc, Mercator)

Fig=plt.figure(figsize=(8,6),edgecolor='w')
m=Basemap(projection='cyl',resolution=None,llcrnrlat=-90,urcrnrlat=90,llcrnrlon=-180,urcrnrlon=180)
DrawMap(m)

這裏我們呼叫了Basemap物件的llcrnrlat,urcrnrlat,llcrnrlon,urcrnrlon參數,來分別指定左下角(llcrnr,lower left corner)和右上角(urcrnr, up right corner)的經度(lon)和緯度(lat)設定

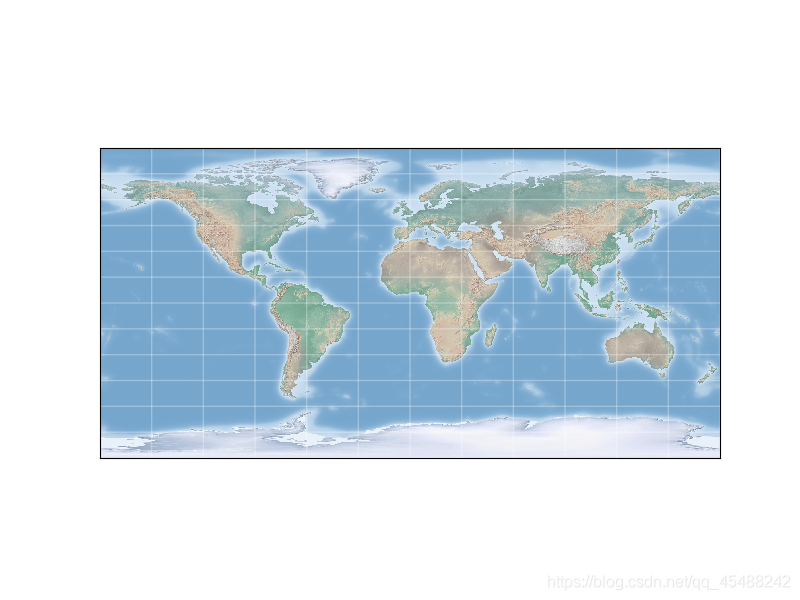
在这里插入图片描述

可以看到格林蘭島的畸變非常嚴重

僞圓柱投影 Pseudo-Cylindrical Projection

僞圓柱投影是在圓柱投影的基礎上進行了改進,經度線不必是豎直的,而可以是彎曲的,這樣將使得南北極地區區域的地形更加真實

例如摩爾威德投影(Moollweide,moll),他所有的經度線都是橢圓弧線

其他的僞圓柱投影還有正弦投影(sinusoidal,sinu),羅賓森投影(Robinson,robin)

Fig=plt.figure(figsize=(8,6),edgecolor='w')
m=Basemap(projection='moll',resolution=None,lat_0=0,lon_0=0)
DrawMap(m)

這裏我們指定lat_0和lon_0來指定地區中心的緯度和經度

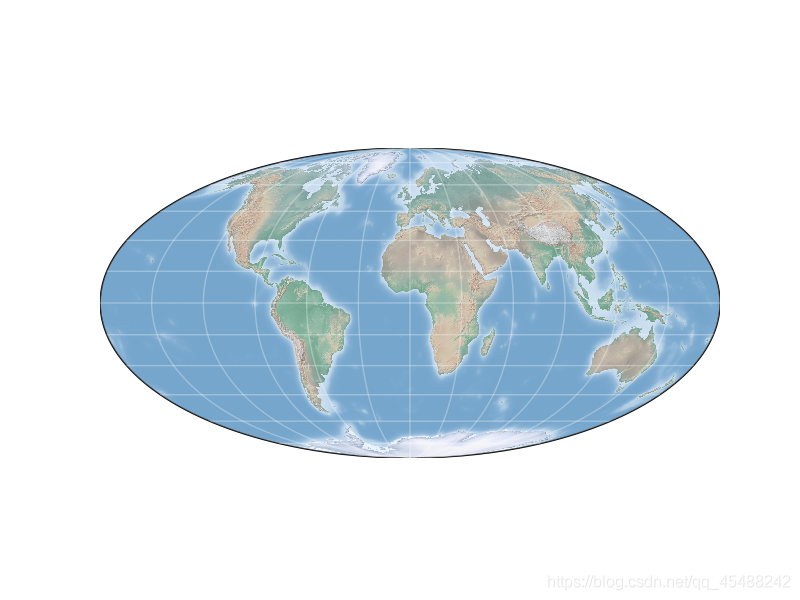
在这里插入图片描述

我們可以看到格林蘭島的外觀稍微好點了

透視投影 Perspective Projection

透視投影是從某一個頭十點對地球進行透視獲得的投影,就好像站在地球晶體空的某一點給地球照相一樣

一個典型的透視投影就是我們前面使用的正射投影(orthographic, ortho),即從無限遠處觀察地球的一側

此外還有球心投影(gnomonic,gnom)和球極平面投影(stereographic,stere)

Fig=plt.figure(figsize=(8,6),edgecolor='w')
m=Basemap(projection='ortho',resolution=None,lat_0=50,lon_0=0)
DrawMap(m)

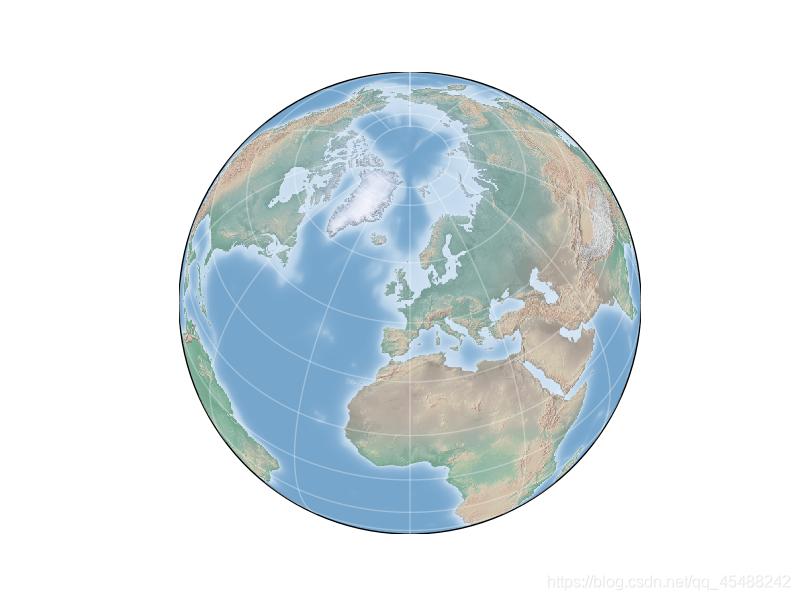
在这里插入图片描述

圓錐投影 Conic Projection

圓錐投影是先將地圖投影成一個圓錐體,然後在將其展開,這樣將獲得非常好的區域性效果,但是距離圓錐頂點較遠的區域會發生嚴重的畸變

典型的例子就是蘭伯特等角圓錐投影(Lambert conforml conic projection, lcc),它指定兩個標準的緯線作爲構成圓錐(分別是lat_1與lat_2)

此外,常用的圓錐投影還有等距圓錐投影(equidistant,eqdc)和阿爾伯斯等積圓錐(Albers equal-area,aea)

Fig=plt.figure(figsize=(8,6),edgecolor='w')
m=Basemap(projection='lcc',resolution=None,lat_0=50,lon_0=0,lat_1=45,lat_2=55,width=1.6E7,height=1.2E7)

DrawMap(m)

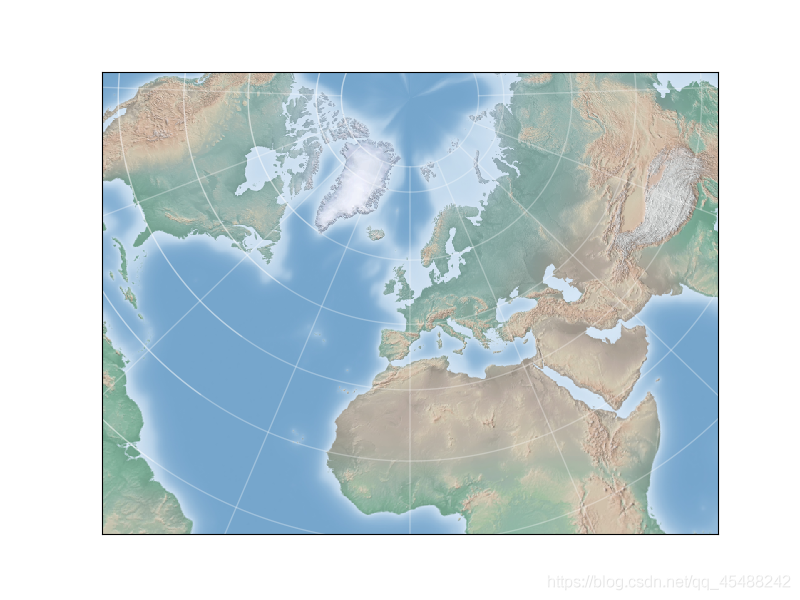
在这里插入图片描述

其他投影型別

實際上在Basemap程式包的介紹文件裡還有更多關於投影型別的介紹,自行查閱即可

Basemap繪製地圖背景

前面介紹,我們可以呼叫Basemap物件的bluemarble()方法和shadedrelief()繪製地球的投影,用drawparallels()繪製緯線,drawmeridians()方法繪製經線

其實我們還有許多地理影象視覺化方法,下面下麪將介紹一些方法

物理邊界與水域
- drawcoastlines(): 繪製大陸海岸線
- drawlsmask():爲陸地和海洋設定填充色,從而可以在陸地或海洋投影其他影象
- drawmapboundary(): 繪製地圖邊界,包括爲海洋填充顏色
- drawrivers(): 繪製河流
- fillcontinents(): 使用一種顏色填充大陸,可選參數用另外一種參數填充湖泊
政治邊界
- drawcountries(): 繪製國界線
- drawstates(): 繪製美國州界線
- drawcounties(): 繪製美國縣界線
地圖特性
- drawgreatcircle(): 在兩點間繪製圓
- drawparallels(): 繪製緯線
- drawmeridians(): 繪製經線
- drawmapscale(): 繪製現行比例尺
地球影象
- bluemarble():繪製NASA藍色彈珠地球投影
- shadedrelief(): 在地圖上繪製地埋暈染圖
- etopo(): 繪製地形暈染圖
- warpimage(): 將使用者提供的影象投影到地圖上

此外,如果我們使用邊界類影象繪製方法,就必須指定解析度.我們可以指定resolution參數來設定解析度,分別是

值	說明
c	原始解析度
l	低解析度
i	中解析度
h	高解析度
f	全畫質解析度

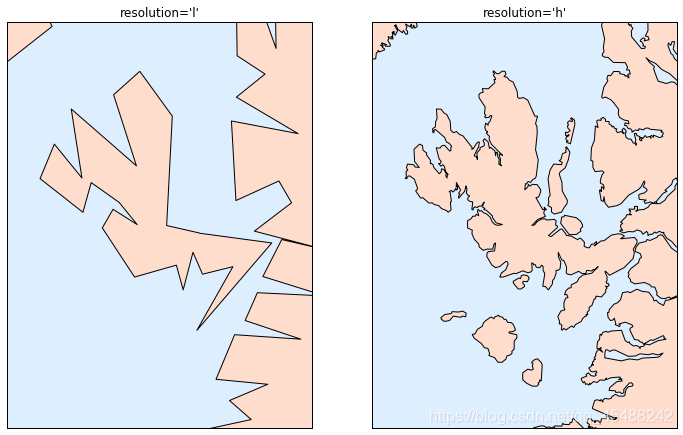
我們繪製一個海岸線爲例

for i,res in enumerate(['l','h']):

    m=Basemap(projection='ortho',lat_0=57.3,lon_0=-6.2,width=90000,height=12000,resolution=res,ax=Axes[i])
    m.fillcontinents(color='#FFDDCC',lake_color='#DDEEFF')
    m.drawmapboundary(fill_color='#DDEEFF',)
    m.drawcoastlines()
    Axes[i].set_title("Resolution='{0}'".format(res))

plt.show()

這裏我們使用Python自帶的enumerate()函數,來將遍歷的物件的元素和索引結合起來,類似於Series

在这里插入图片描述

Basemap在地圖上繪製數據

最後,Basemap中最實用的功能就是以地圖爲背景繪製各種數據

我們可以使用任意的plt函數來繪製圖形和文字,當然,我們需要將直角座標轉化爲球面座標

實際上Basemap物件中有許多方法也可以繪製地圖,只不過多了latlon參數,如果我們將其設定爲True,就表示使用原來的經緯度座標,而非直角座標

Basemap對現代格部分繪圖方法如下:

contour() / contourf() : 繪製等高線 / 填充等高線
imshow() : 繪製圖像
pcolor() / pcolormesh() : 繪製帶規則 / 不規則網格的僞彩圖
plot() :繪製線條和散點
scatter() : 繪製帶標籤的點
quiver() : 繪製箭頭
barbs() : 繪製風羽
drawgreatcircle() : 繪製大圓圈

下面下麪我們用前面使用過的美國加州城市數據爲例,繪製散點圖

cities=pd.read_csv('california_cities.csv')

cities_lat=cities['latd'].values
cities_lon=cities['longd'].values
cities_population=cities['population_total'].values
cities_area=cities['area_total_km2'].values

Fig=plt.figure(figsize=(8,8))

m=Basemap(projection='lcc',resolution='h',lat_0=37.5,lon_0=-119,width=1E6,height=1.2E6)
m.shadedrelief()
m.drawcoastlines(color='gray')
m.drawcountries(color='gray')

m.scatter(cities_lon,cities_lat,latlon=True,c=np.log10(cities_population),s=cities_area,cmap='Reds',alpha=0.5)

plt.colorbar(label=r"$\log_{10}({\rm population})$")
plt.clim(3,7)
for a in [100,300,500]:
    plt.scatter([],[],c='red',alpha=0.5,s=a,label=str(a)+'km$^2$')
plt.legend(scatterpoints=1,frameon=False,labelspacing=1,loc='lower left')

plt.show()

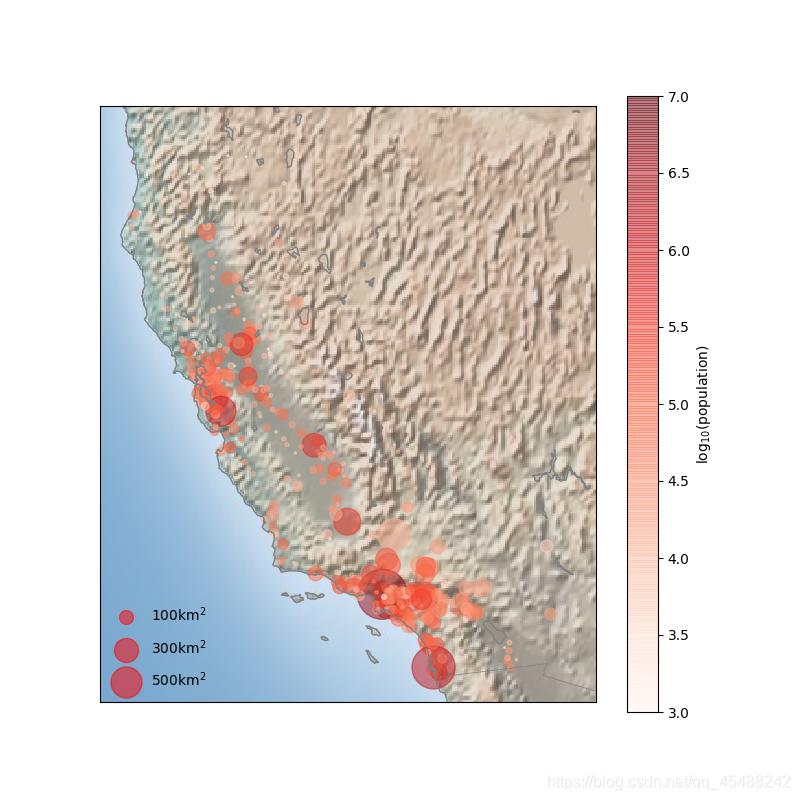
在这里插入图片描述

我們可以發現,加州所有的城市都沿着平坦的中央谷地的高速公路延伸,幾乎完全避開了加州的山區地帶

6.Matplotlib繪製高階影象:Basemap和Mplot3D

文章目錄

Matplotlib繪製高階影象

Matplotlib繪製三維影象

指定projection參數建立三維子圖

Axes3D.plot3D()與Axes3D.scatter3D()繪製三維點與線

Axes3D.contour3D()繪製三維等高線圖

Axes3D.plot_wireframe()繪製線框圖

Axes3D.plot_surface()繪製曲面圖

Axes3D.plot_trisurf()擬合曲面

案例:莫比烏斯環

Matplotlib使用Basemap繪製地圖影象

安裝Basemap

Basemap的基礎概念

藍色彈珠

球面座標

Basemap的投影方式

圓柱投影　Cylindrical Projection

僞圓柱投影 Pseudo-Cylindrical Projection

透視投影 Perspective Projection

圓錐投影 Conic Projection

其他投影型別

Basemap繪製地圖背景

Basemap在地圖上繪製數據

6.Matplotlib繪製高階影象:Basemap和Mplot3D

文章目錄

Matplotlib繪製高階影象

Matplotlib繪製三維影象

指定projection參數建立三維子圖

Axes3D.plot3D()與Axes3D.scatter3D()繪製三維點與線

Axes3D.contour3D()繪製三維等高線圖

Axes3D.plot_wireframe()繪製線框圖

Axes3D.plot_surface()繪製曲面圖

Axes3D.plot_trisurf()擬合曲面

案例:莫比烏斯環

Matplotlib使用Basemap繪製地圖影象

安裝Basemap

Basemap的基礎概念

藍色彈珠

球面座標

Basemap的投影方式

圓柱投影 Cylindrical Projection

僞圓柱投影 Pseudo-Cylindrical Projection

透視投影 Perspective Projection

圓錐投影 Conic Projection

其他投影型別

Basemap繪製地圖背景

Basemap在地圖上繪製數據

圓柱投影　Cylindrical Projection