如果讓你來設計訊息加密
你是跑碼場的一個程式設計師,名字叫招財。
利用上班摸魚的時間編寫了一個簡易的即時通訊軟體,並行布到了網上。過了一段時間,你在軟體上突然收到一條私信。
「小哥哥,我很喜歡你寫的這個軟體,我也是程式媛,希望以後能多多和您交流。」
你望了望四周,沒有人表現得異常,於是你確認不是同事在逗自己。
你興沖沖地給對方回覆,一來二去,慢慢熟識了起來。你知道了對方的名字,叫小美。
1、不安全的明文
隨著交流的話題越來越深入,你也慢慢變得惶恐。你本來就是隨手寫著玩兒的軟體,訊息都是明文傳送的,這萬一被研究網路的同事給監聽了,以後在公司還怎麼混?
於是你想到了:加密。
2、對稱加密
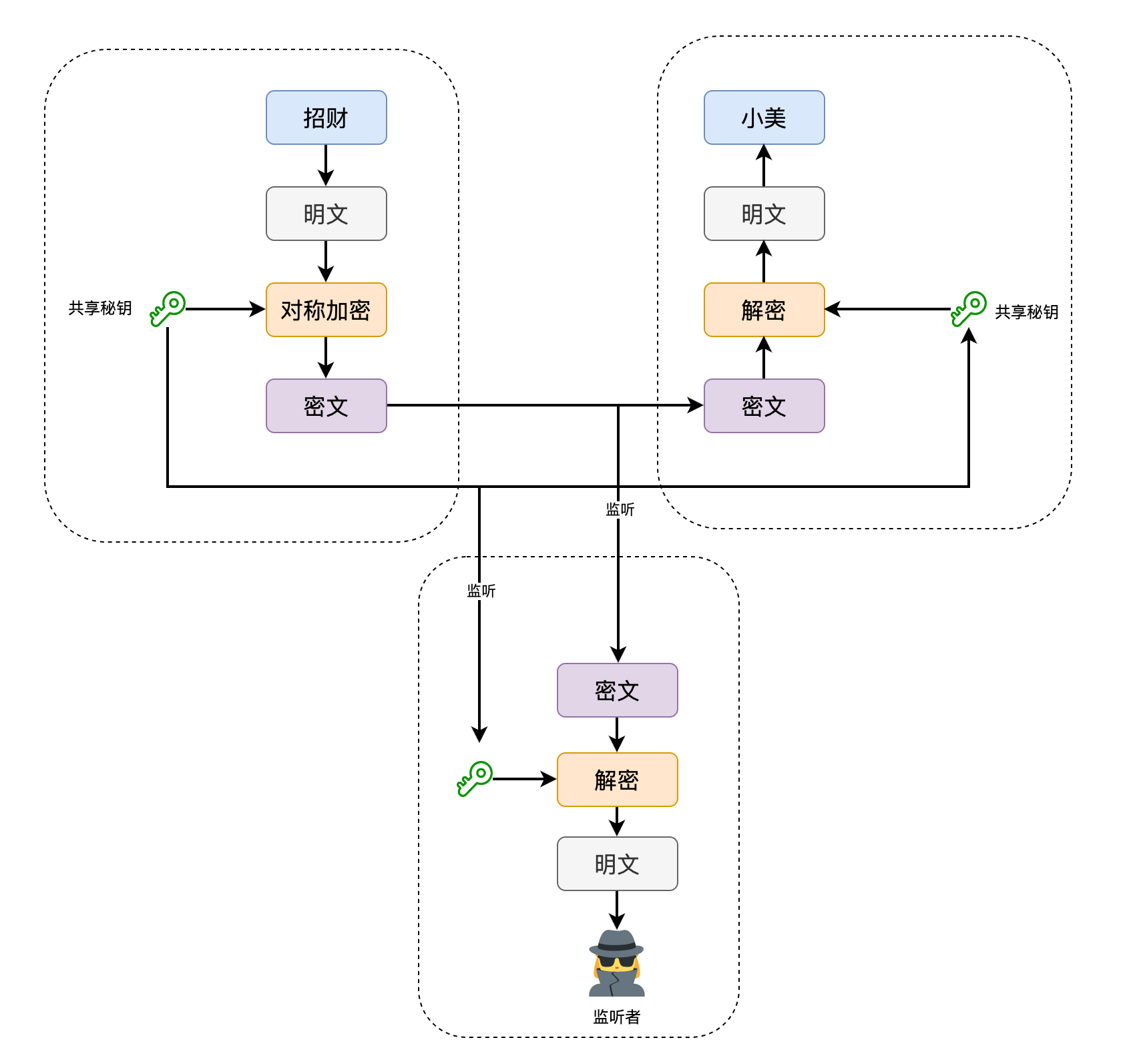
如果雙方擁有同樣的鑰匙,傳送訊息的一方使用這個鑰匙進行加密,接收訊息的一方使用同一個鑰匙進行解密。這麼一來,加密的事情就變得簡單了。
為了實現這個功能,你想到了之前學過的互斥或(XOR)操作,這個操作的規則總結起來就是:相等為0,不等為1。任何資料在計算機中都會最終表示為01的位元組流,比如你想傳送的訊息被最終編碼為1001110011001110,然後隨機生成一個同樣長度的字串1011011100110011,稱為祕鑰,兩者做一下互斥或操作:
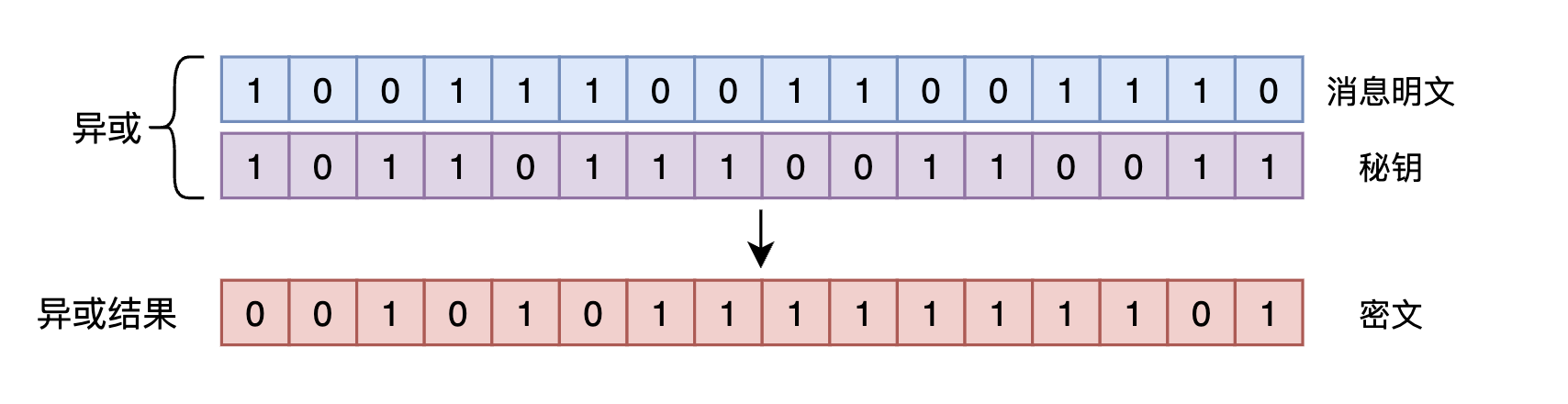
訊息明文與祕鑰進行互斥或操作之後就得到了密文,按照互斥或運算的性質,如果此時將密文再和祕鑰做一次互斥或操作,那麼將重新得到訊息明文。
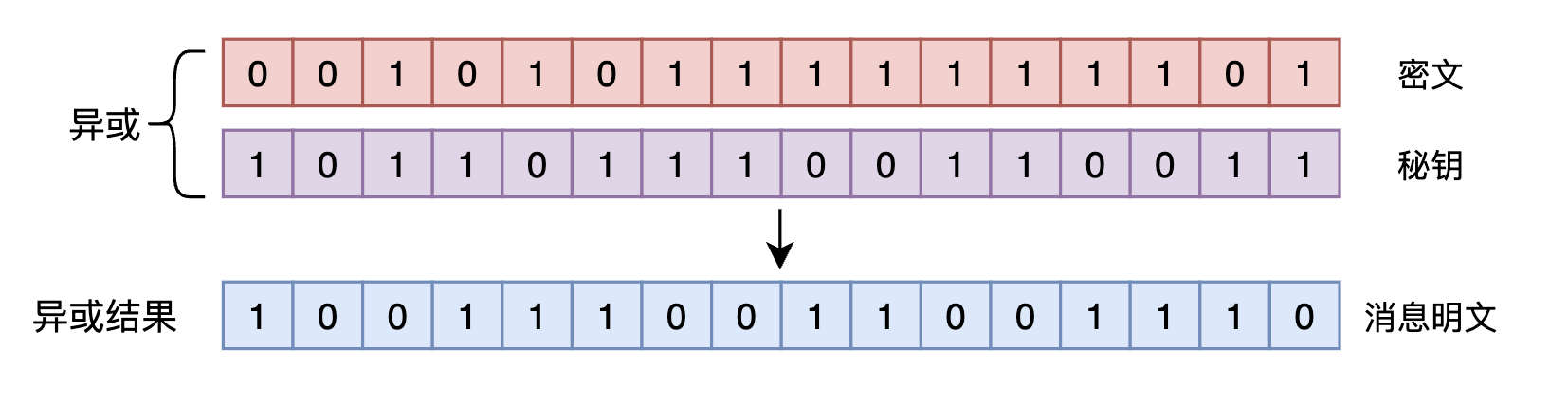
如此一來便實現了雙方使用同一個共用祕鑰對訊息進行加密/解密的操作。
但是目前有個問題,你生成的祕鑰長度必須和訊息的長度保持一致才能做互斥或操作,除非你對互斥或操作進一步封裝。你才懶得琢磨這些東西呢,於是上網找思路。
這才知道,你的想法其實就是對稱加密。DES、3DES以及AES密碼演演算法都屬於對稱加密,其中或多或少都利用了互斥或運算的性質,否則就沒有了「對稱」的效果。
你選擇了目前最流行的AES演演算法,打算直接使用現成的類庫實現加密。你把這個想法告訴了小美,迫不及待地想讓她知道你們的對話已經實現了機密性。
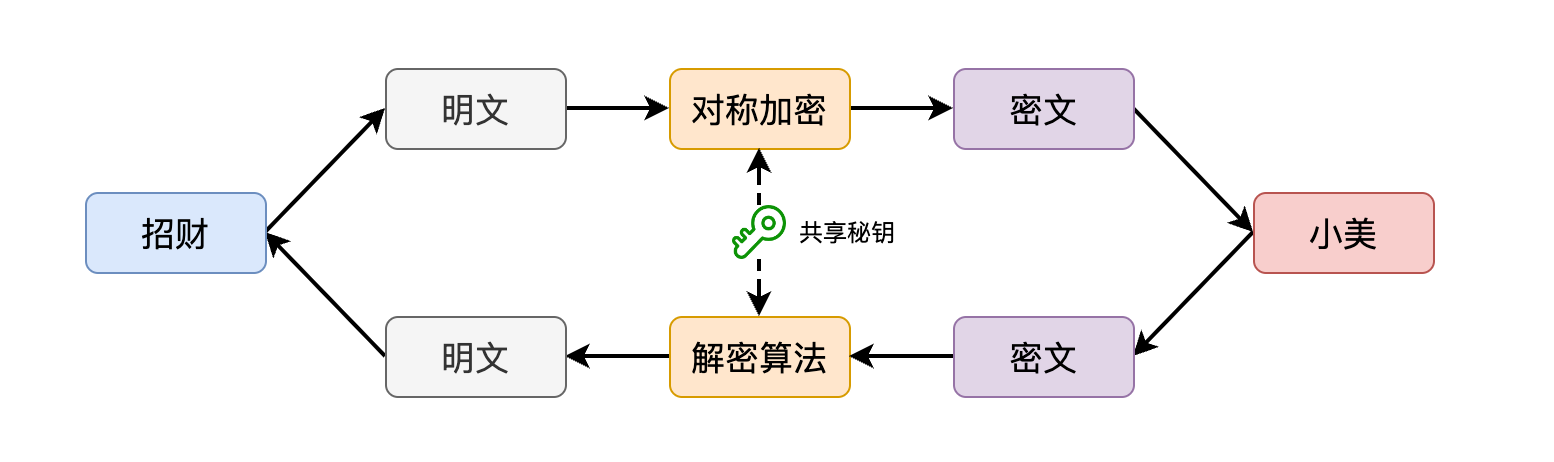
誰知,小美一針見血地指出了問題,「祕鑰如何安全地在我們之間進行共用呢?」
是啊,監聽者也是可以獲取到祕鑰的。這樣就很矛盾,如果有一個辦法能將祕鑰安全地共用出去,那麼豈不是也可以用同樣的方法來安全地傳送明文咯?
對稱密碼的祕鑰必須傳送,而又不能明文傳送,這就是對稱祕鑰的配送問題。
3、非對稱加密
於是你又開始尋找其他方法,終於發現了一種叫做公鑰密碼的演演算法。
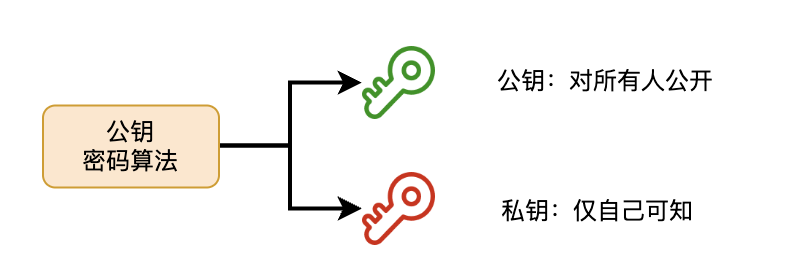
這種演演算法可以生成一組金鑰對,分別叫做公鑰和私鑰。正如其名字暗示的那樣,公鑰是可以公開的,地球人都可以知道,而私鑰必須自己儲存好,打死也不能讓別人知道的。
由公鑰進行加密的密文,必須使用與該公鑰配對的私鑰才能夠解密。反過來,使用私鑰進行加密的密文,擁有公鑰的人都可以進行解密。這個特點非常重要。
於是你生成了一組金鑰對,並將公鑰發給了小美,自己儲存好私鑰。你讓小美給你傳送訊息之前先用你的公鑰對訊息進行加密,這樣一來,小美的加密訊息只有你的私鑰才能夠解密。
於是便實現了小美對你傳送訊息的機密性。
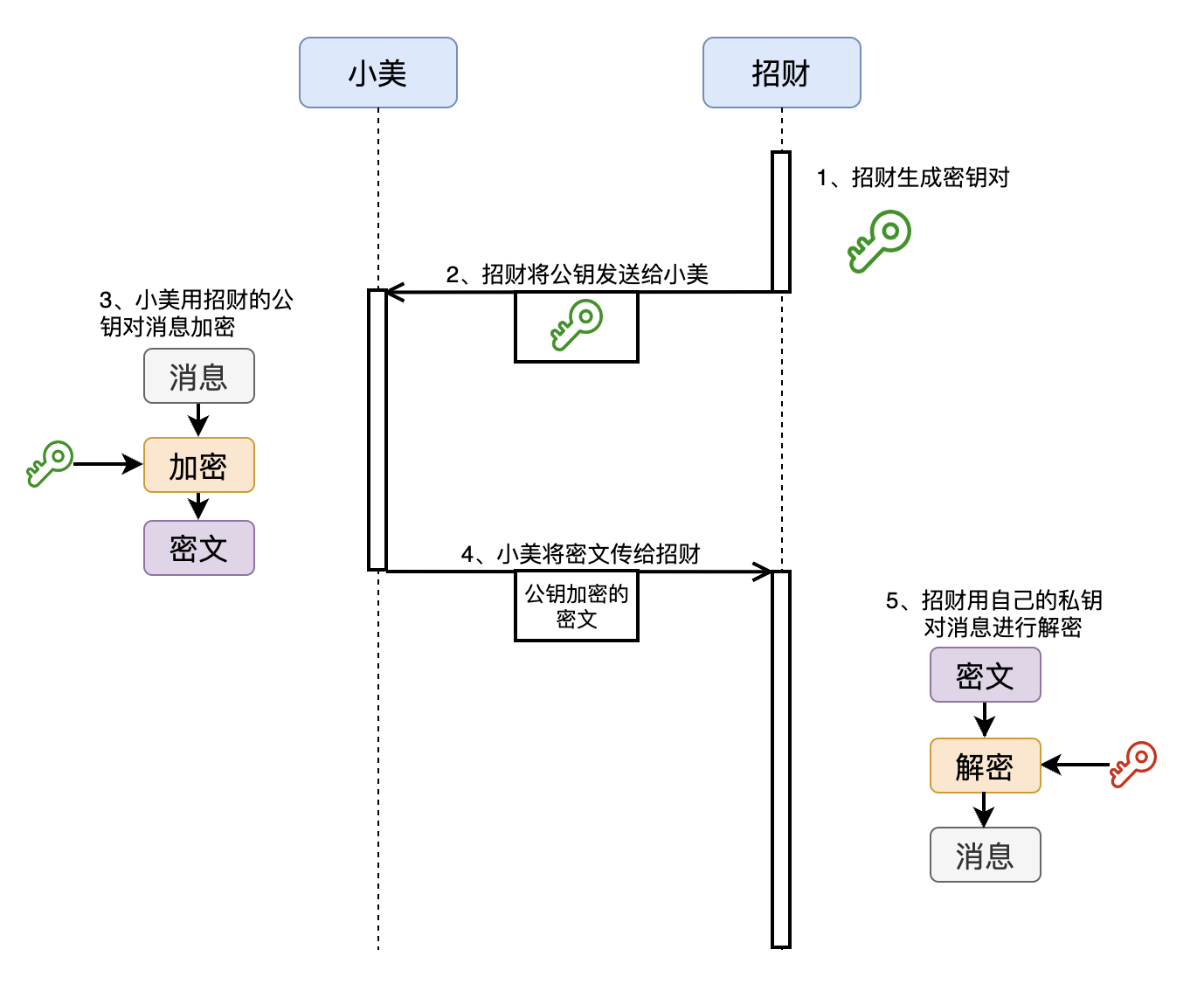
反過來,如果要實現你對小美傳送訊息的機密性,就需要小美生成一組金鑰對,你獲得小美的公鑰,然後傳送訊息之前首先用小美的公鑰對訊息進行加密,將密文傳送給小美之後,小美再用她的私鑰進行解密。
如果通訊過程中的公鑰和密文被監聽者獲取到也沒關係,因為你們兩人的私鑰都沒有出現在通訊過程中,監聽者即使有了密文也沒法解密。
這樣一來,你通過了公鑰加密解決了訊息的機密性和祕鑰的配送問題(因為壓根不需要配送對稱加密的祕鑰了)。
公鑰密碼還有一個名字,叫做非對稱加密。這個名字是相對對稱加密而言的。
對稱加密是使用同一個祕鑰進行相反的運算,因此對稱密碼中的加密和解密就像照鏡子一樣,是相互對稱的。非對稱加密中,加密和解密使用的是不同的金鑰,並非相互對稱,因此稱為非對稱加密。
注:大名鼎鼎的
RSA演演算法和ECC(橢圓密碼曲線)演演算法都是公鑰密碼演演算法的具體實現
4、混合加密演演算法
公鑰加密的改進讓你感到非常踏實,現在滿腦子裡裝的都是跟小美聊天。可是你逐漸發現,小美的回覆變得比之前慢了一些。
和小美溝通一番之後發現,她對你的回覆也有同樣的感覺。
聰明的你最終發現了原因,公鑰加密的演演算法效率太低下了!在採用具備同等機密性的金鑰長度的情況下,公鑰加密的速度只有對稱加密的幾百分之一。
知道了問題,解決方案也是很明顯了,把對稱加密和公鑰加密結合起來使用,也就是混合加密。
既然是混合加密,自然既要傳送訊息,又要傳送對稱加密的祕鑰。你先用加密效率很高的對稱加密演演算法對訊息進行加密,這樣就實現了訊息的機密性。接下來只要保證對稱加密祕鑰傳輸的機密性就可以了。
這時候又要用到公鑰加密了。你將對稱加密的祕鑰當做訊息,利用上文公鑰加密的步驟,先使用小美的公鑰對對稱加密的祕鑰進行加密,小美收到之後再用自己的私鑰進行解密,就能安全在你倆之間傳遞對稱加密的祕鑰了。
你也不用擔心效率問題,畢竟對稱加密的祕鑰通常比訊息短得多,況且祕鑰的傳遞只需要一次就可以了,因此加密的時間代價可以忽略。
畫一下使用混合加密演演算法時,你傳送訊息進行加密的流程圖。
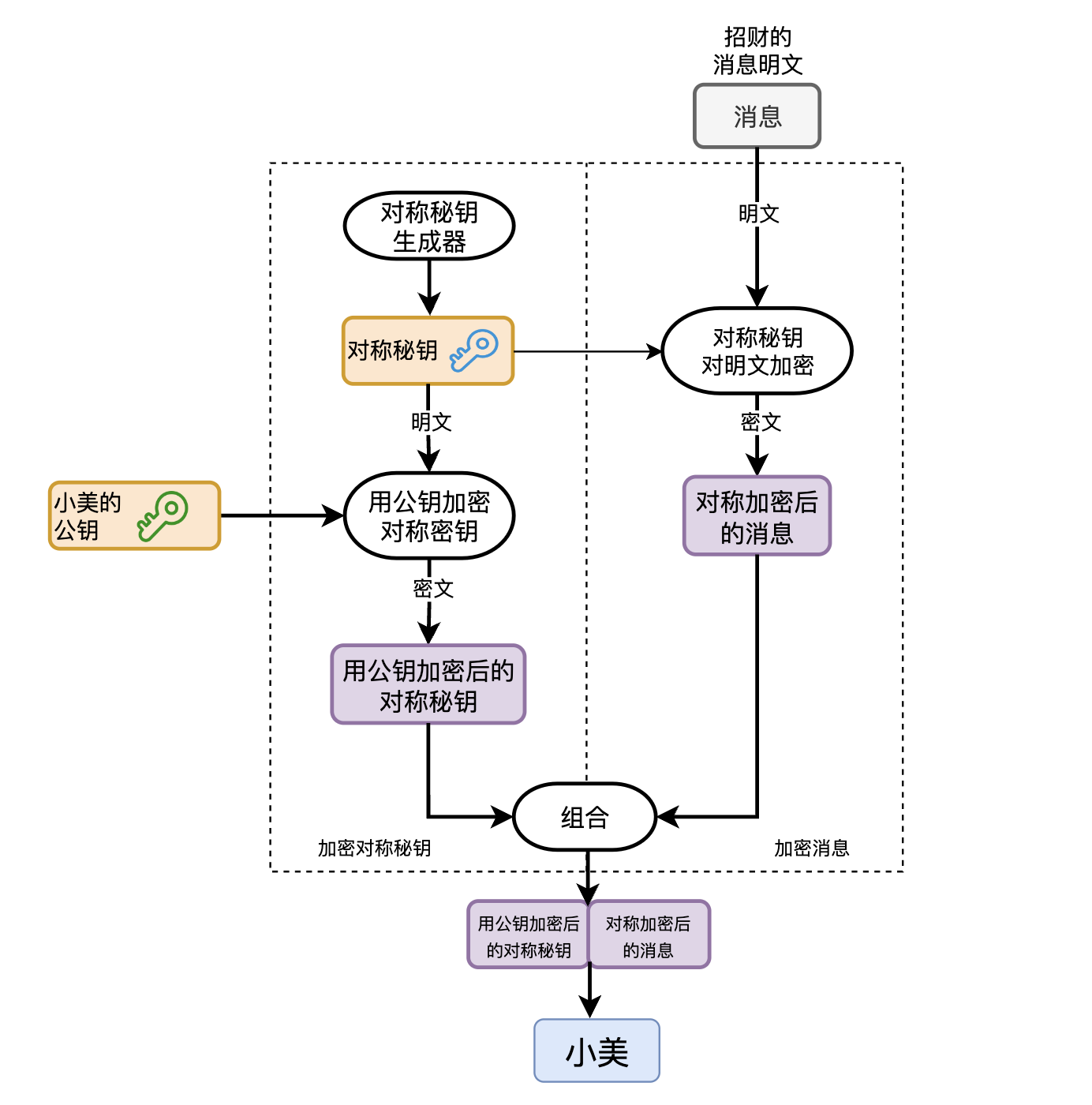
懂了加密,解密也就很簡單了,為了讓小美看得明白,你還是給她畫了個解密流程圖。
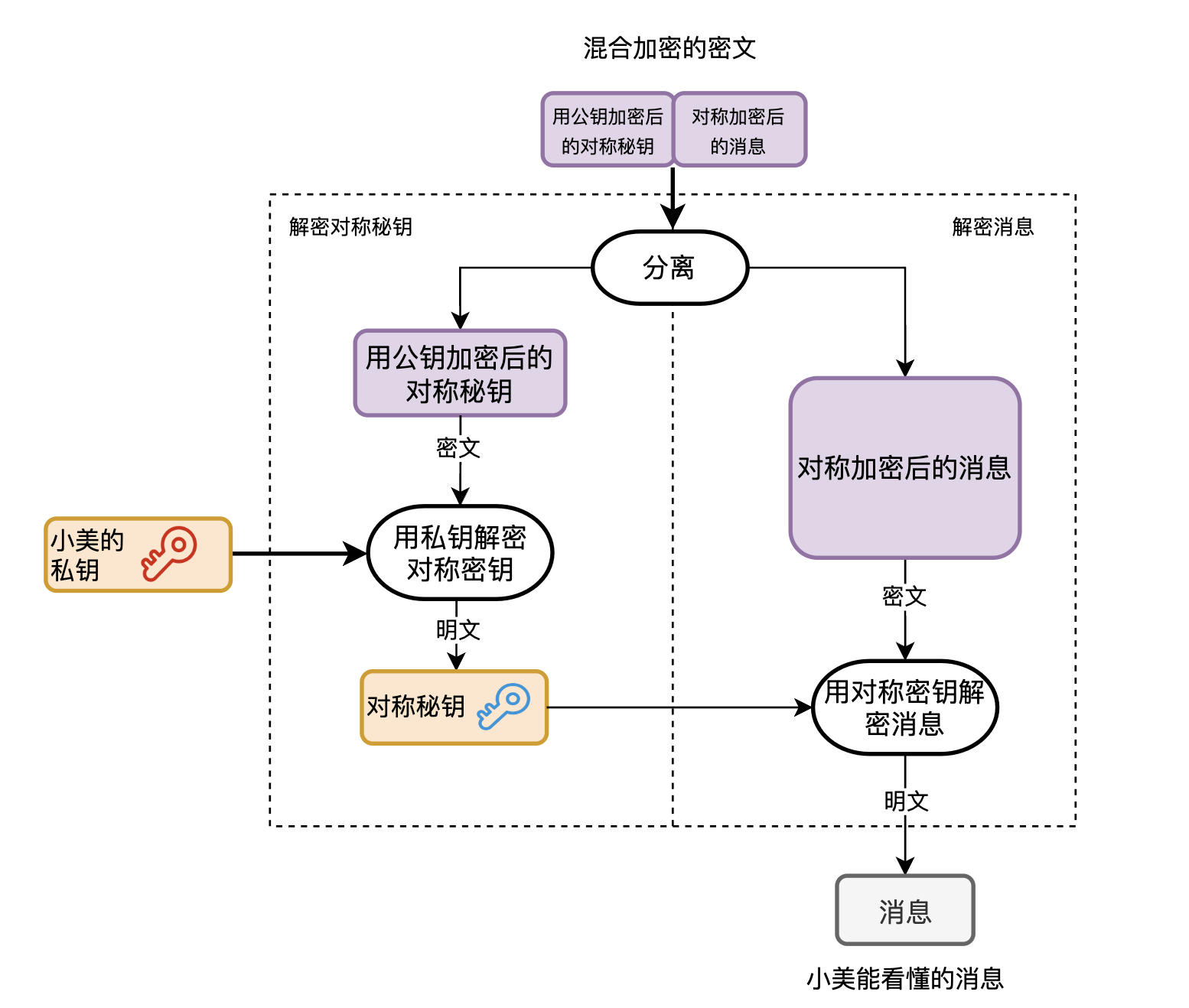
到此為止,你解決了公鑰加密速度慢的問題,並通過公鑰加密解決了對稱祕鑰的金鑰配送問題。
5、誰改了我的訊息
你和小美聊得愈發火熱。但是你最近總是時不時收到小美髮過來的莫名其妙的文字。你開始不以為意,但是這種文字的傳送頻率越來越高,實在搞得你頭大。
你趕緊問了問小美,在確定不是她故意發這種文字之後,你明白了。
你倆被人盯上了。。。
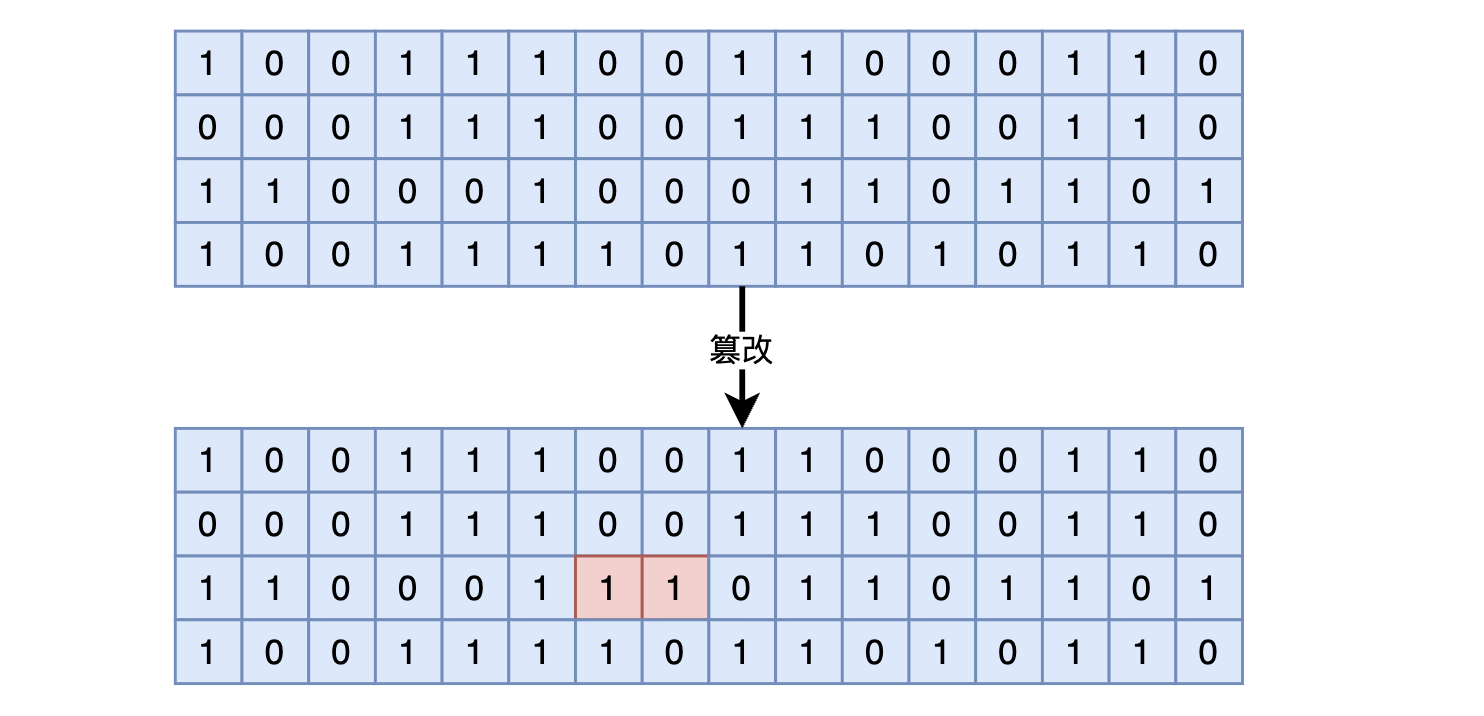
你分析了一下小美實際傳給你的加密訊息與你實際收到的加密訊息,發現編碼之後的資料有兩位位元被改變了。改變雖然不大,但是對訊息的可讀性會造成相當大的影響。
你遇到中間人攻擊了。
這種情況下,中間人不需要知道你倆聊得究竟是什麼,只需要擷取你們的訊息,然後進行隨意篡改,就能擾亂你倆之間的正常交流。
你不禁感嘆:怎麼傳遞個訊息就這麼難呢!
好在這個問題不難解決,你馬上就想到了單向雜湊演演算法。
單向雜湊演演算法可以對任意長度的訊息生成一個固定長度的一串資料(雜湊值),這串資料的長度遠小於輸入的訊息長度,因此又被稱為訊息摘要,單向雜湊演演算法也因此被稱為訊息摘要演演算法。
摘要演演算法可以實現訊息的完整性檢查。
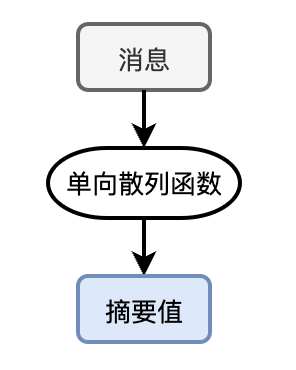
訊息摘要演演算法的一個巨大好處是對訊息的變化極為敏感,哪怕對訊息僅修改了1個位元,生成的訊息摘要也會有翻天覆地的變化。而且,即使中間人截獲了摘要訊息,他想自己偽造一個經過雜湊能夠生成同樣摘要的訊息幾乎是一件不可能的事情。
注:經常聽到的
MD5、SHA-1、SHA2、SHA3演演算法都是訊息摘要演演算法的具體實現
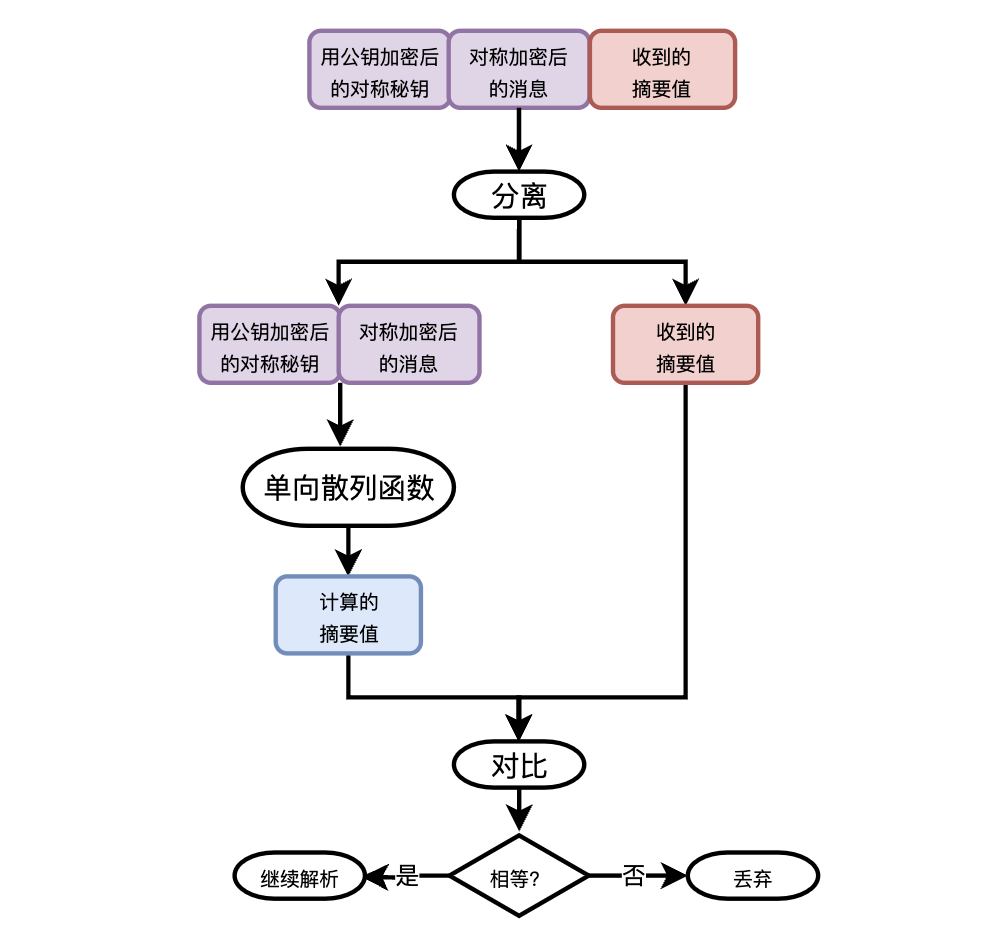
於是你在訊息傳送和解析過程中又新增了對訊息摘要演演算法的支援。傳送資料之前,先對混合演演算法加密之後的密文計算摘要值,然後將摘要值附在密文的最後,一起傳輸給小美。
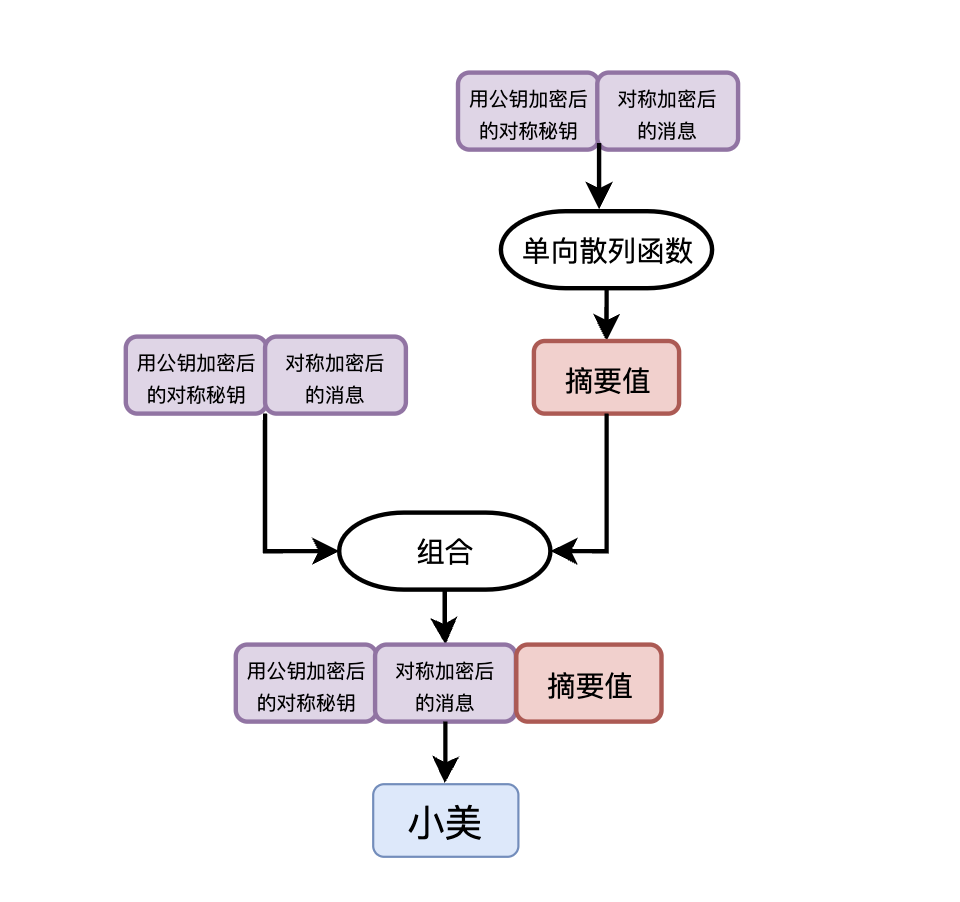
小美收到資料後,根據資訊摘要的固定長度,首先分離摘要值和密文,然後使用相同的摘要演演算法計算出密文的摘要,與接收到的摘要進行對比,一致則表示資訊沒有被篡改,否則就說明被動了手腳,直接丟棄。
你認為事情到這終於結束了。但是軟體更新之後,你發現還是會時不時收到莫名其妙的訊息。
6、是誰在冒充
你思來想去,問題到底出在了哪裡?
「會不會是我們的訊息整個都被篡改了啊。」小美說道。「如果中間人監聽到了整個訊息,分離出了混合加密的密文和摘要值,然後篡改混合加密的密文,再重新對篡改之後的密文計算出一個新的摘要,附在篡改的密文之後再傳送,我們根本無法識別出篡改。」
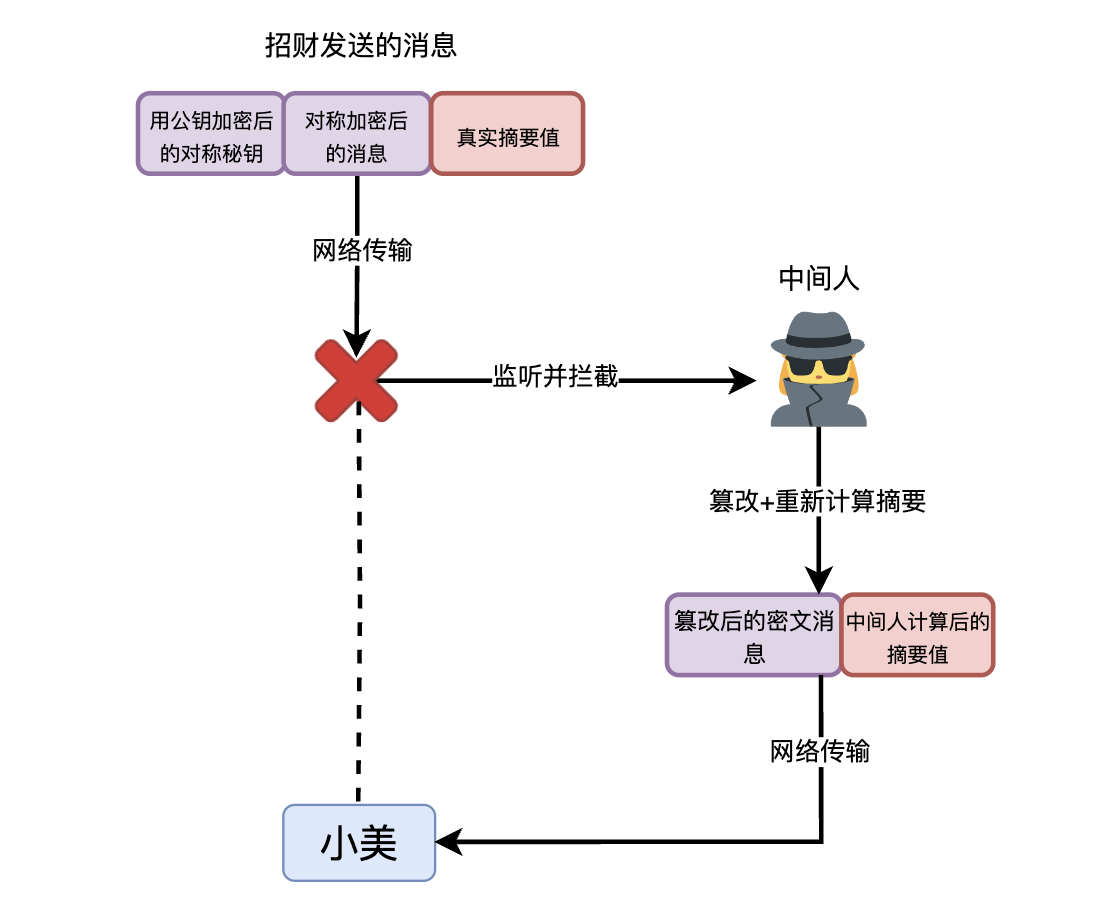
是啊,如果真的是這樣,摘要值檢查的實際上就是中間人傳送的訊息的完整性,這個檢查就失去了意義。
現在中間人已經徹底挾持了通訊線路,只要中間人想,他就能篡改你們之間的所有資料。換句話說,你現在根本不知道和你進行通訊的是小美還是中間人。
這就是單向雜湊函數的缺陷,能夠辨別出「篡改」,但是無法分辨出「偽裝」。
你現在需要實現訊息的認證功能。也就是說,你對小美傳送的訊息,需要向小美證明訊息確實是你發的,並且沒有被篡改。同樣,小美對你傳送的訊息,也需要向你證明,訊息確實是小美髮的,並且沒有被篡改。
7、確認對方身份
於是你跟小美商量,需要約定一個只有你們兩人才知道的「資訊」,並且通過接收到的訊息可以判定,只有擁有這個共同資訊的彼此才能發出這條訊息。
小美立刻想到,「我們一直在使用的對稱加密的祕鑰不就是這個「共同資訊」嘛!如果我發的訊息你能解密出來,不就證明我就是我了嗎?」
「你這麼想從一定程度上是對的,但是有個前提條件,就是你發的訊息一定是有意義的。如果你本身就是想給我傳送一堆亂七八糟的文字,我無法確定這是你的本意,還是說訊息已經被中間人篡改了。」
你倆陷入了短暫的沉默。
你思考了一下,摘要值目前無法發揮認證的作用是因為只要中間人獲取到了密文,就能隨便生成摘要值。那如果給摘要值的生成提高門檻,只有擁有「共同資訊」的彼此才能夠生成正確的摘要值,這樣的話不就能認證了嘛。
這個摘要值就叫做訊息鑑別碼。
網上搜尋了一番,還真有這種方法,叫HMAC(Hash Message Authentication Code,雜湊訊息鑑別碼),是用單向雜湊函數來構造訊息鑑別碼的一種方法。
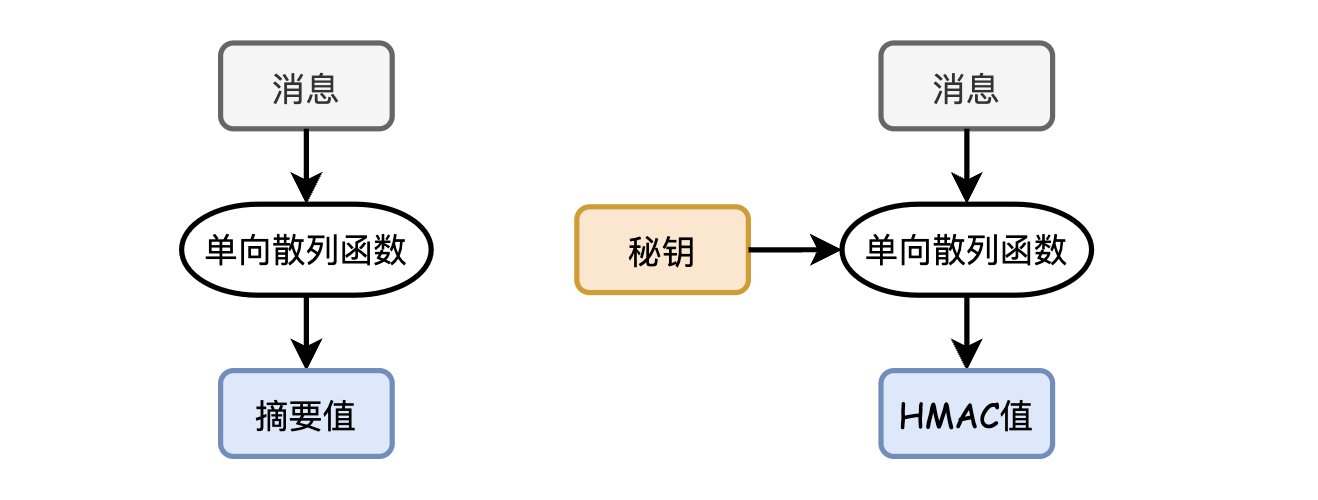
摘要值和HAMC值的最主要的區別就是後者在進行單向雜湊的時候,需要用到一個祕鑰。因此這個可以簡單理解為,訊息鑑別碼是一種與祕鑰相關聯的單向雜湊函數。
有了這個技術,再來看一下你給小美傳送訊息的過程。
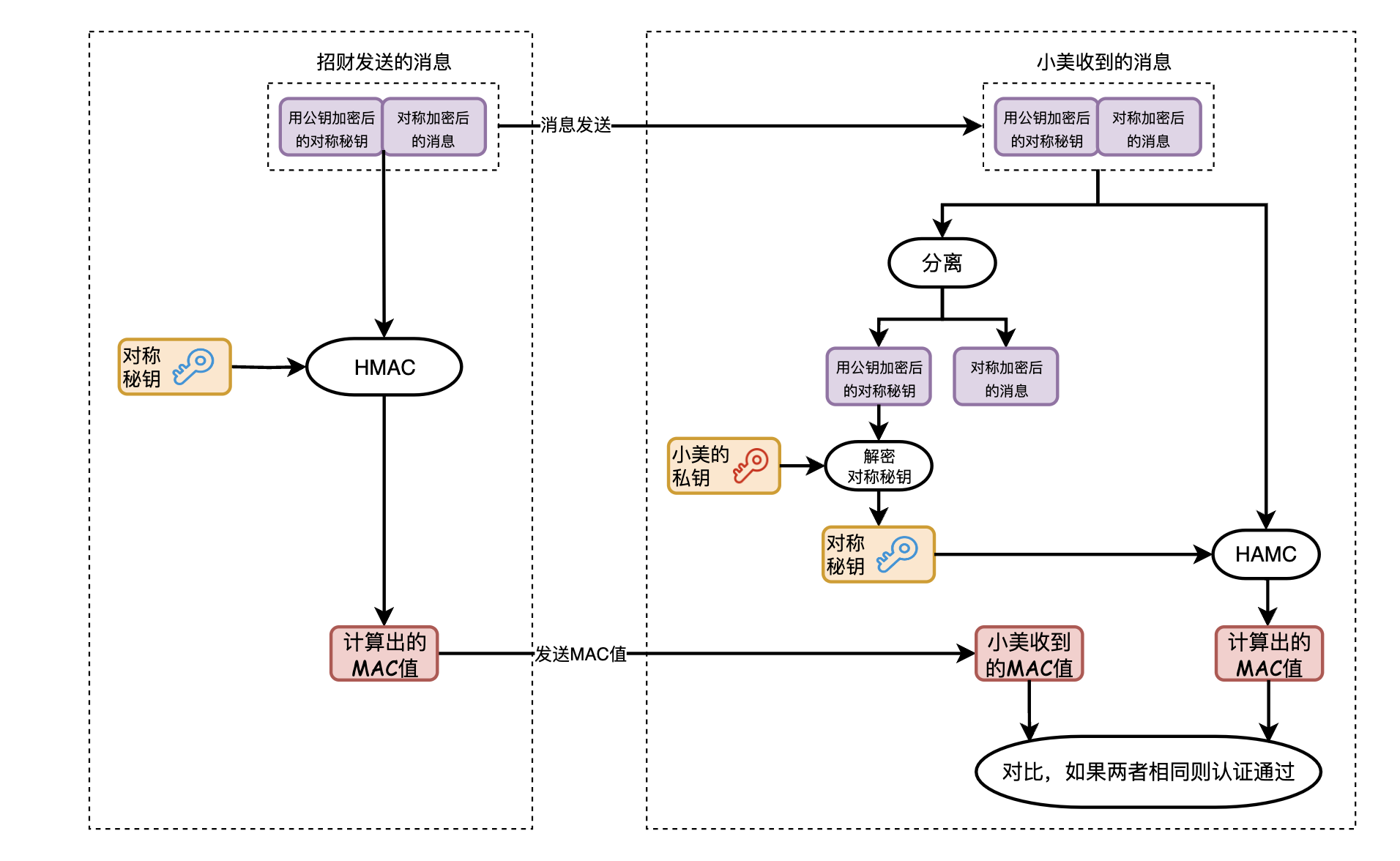
本來應該為HMAC單獨生成一個隨機祕鑰,但是又會涉及到祕鑰配送的問題。由於我們之前已經使用公鑰解決了祕鑰配送問題了,為了方便,就直接使用對稱祕鑰作為HMAC的祕鑰了。
和原來不同的是,用計算出的MAC代替了原來的摘要值,小美接收到密文和摘要值之後。利用自己的私鑰解密獲得對稱加密的祕鑰,再利用這個祕鑰對收到的密文計算MAC值,如果兩個MAC一致,那麼小美就可以確定這個訊息是你傳送的,沒有經過中間人篡改。
如此一來,使用MAC值就實現了訊息的完整性校驗和身份認證的功能。
8、對方死不認賬了
突然有一天,小美對你發來了一條訊息。
「PHP是世界上最好的語言~」
你當場炸裂啊~說這話妥妥引戰嘛,你剛要和小美理論一下,小美緊接著來了句:「我跟你玩個遊戲啊。」然後又傳送了一個調皮的表情。「你如何證明我對你說了這句話呢?」
「這還需要啥證明啊,我用咱倆共用的祕鑰,生成了MAC值,然後和你發給我的MAC對比,是一致的。如果你的私鑰沒有洩露,我就敢絕對保證,這條訊息就是你發的!」
「沒錯,在咱倆之間,是絕對能保證身份的認證的。但是我的問題是,你如何向其他人證明這個訊息是我傳送的呢?你想啊,你和我有相同的祕鑰,也就是說,理論上這條訊息你也能生成。我要是死不認賬,你怎麼辦?當然咯,截圖可不算哈~」
小美說得沒錯,按照現在的加密設計,的確沒法向第三方證明她說過的話。
現在你倆之間能相互認證是由於擁有同一個祕鑰,你確定不是自己發的,那必然就是對方發的。如果想向第三方證明訊息是小美髮的,那就必須使用小美獨有的資訊對訊息做一下處理。
就好比古代的虎符,如果小美持有其中一半,並且保證私有,這樣不管另一半在誰的手裡,只要兩部分能夠合二為一,就能確認對方就是小美。

這不就是公鑰和私鑰嘛!
小美用自己的私鑰對訊息計算出一個「簽名」,任何持有小美公鑰的人都沒辦法用公鑰復刻這個簽名,但是可以對小美傳送的簽名用公鑰進行解密,解開的內容如果恰好就是訊息本身,那說明收到的訊息一定屬於小美!畢竟私鑰是獨一無二的,這下子小美就再也沒辦法否認了!
但是有個小問題,公鑰加密的效率實在是太低了,如果對整個訊息使用私鑰進行加密,耗時太久。能不能找個比較短的資料來代替訊息本身呢?
老朋友——單向雜湊函數,又該出馬了。只要先用單向雜湊函數求出訊息的雜湊值,然後使用私鑰對雜湊值進行簽名就可以了。雜湊值可比訊息本身短得多,因此對其進行簽名的時間代價就小得多了。
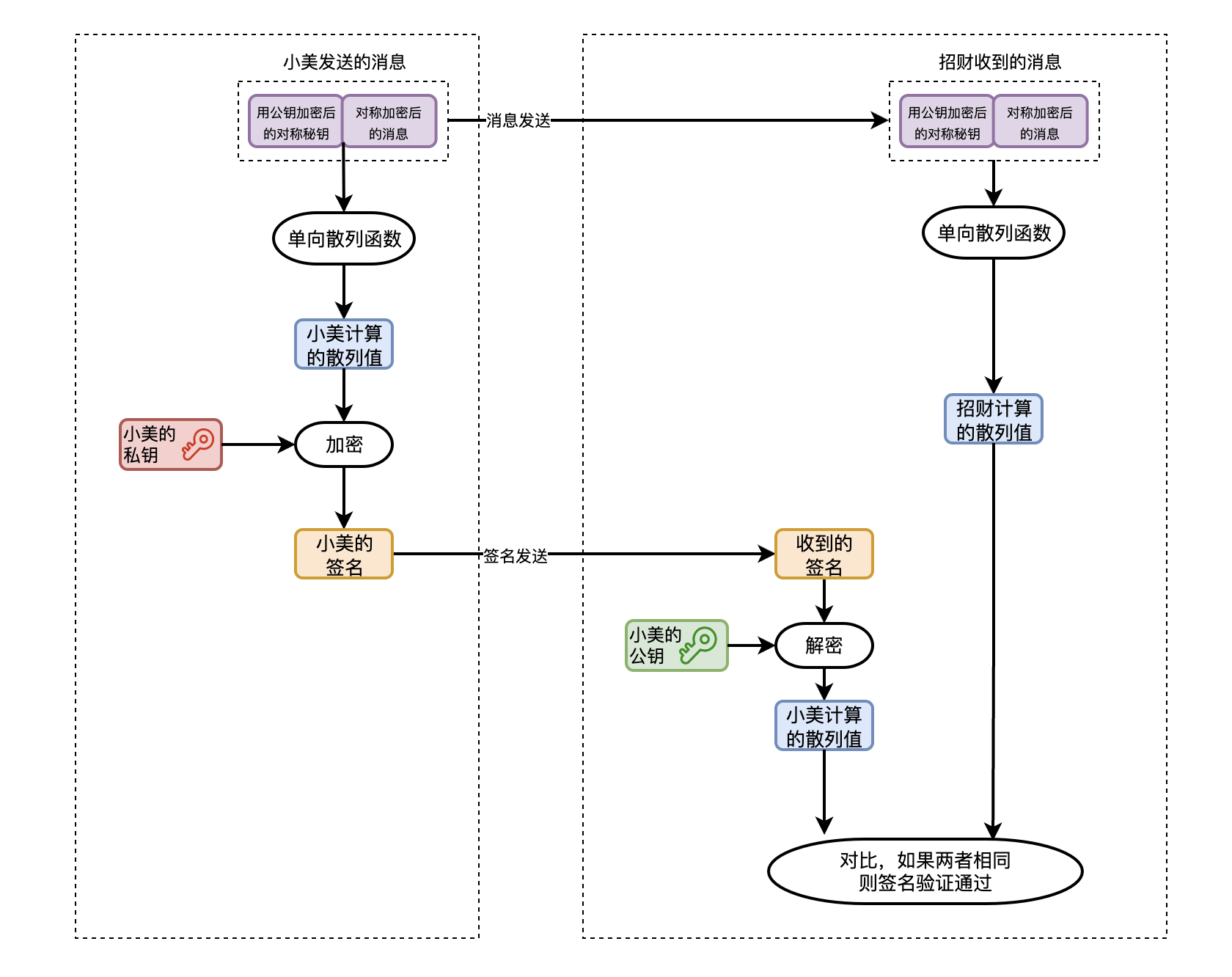
如果中間人篡改了小美傳送的訊息,那麼你計算出來的雜湊值就會發生變化,導致簽名驗證失敗,簽名保證了訊息的完整性和對方身份的認證。不僅如此,簽名還能防止小美否認之前發的訊息。
從圖中可以看出,簽名已經徹底替換掉了之前使用的訊息驗證碼。
到此為止,你已經實現了訊息的機密性、完整性、身份認證以及不可否認性。
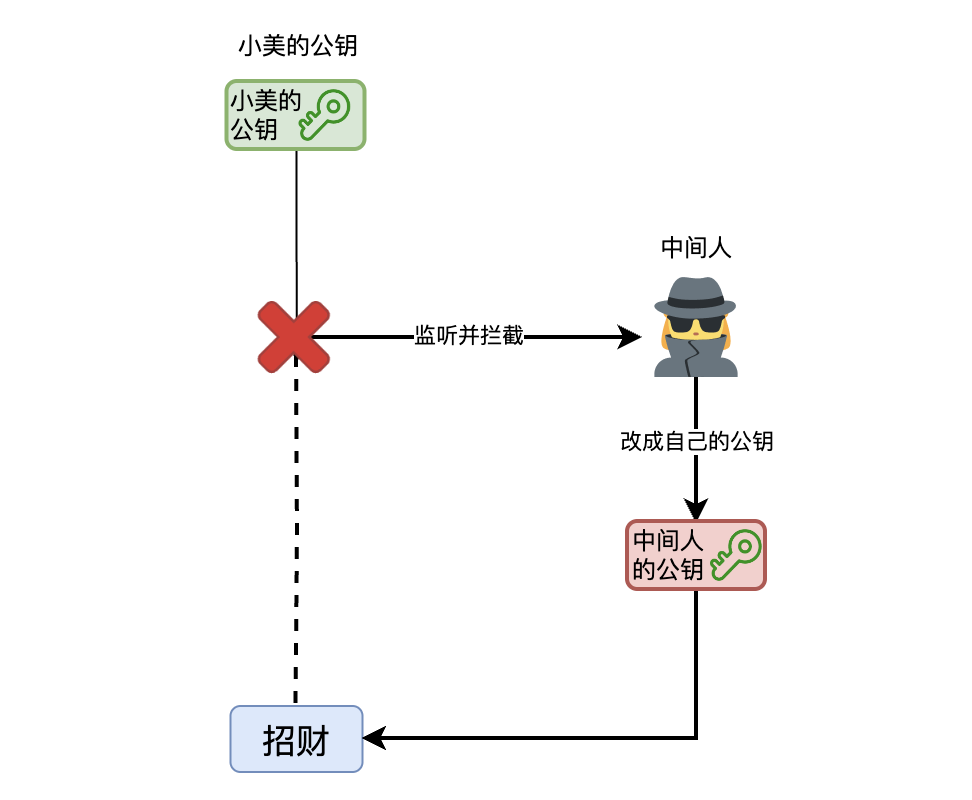
居然不知不覺已經走了這麼多路,你不禁問自己,到簽名這一步已經完美了嗎?簽名的驗證依賴於訊息傳送者公開的公鑰,那如果從一開始,這個公鑰就被中間人劫持,換成了中間人自己的公鑰了呢?我們又該如何確保收到的公鑰沒有被篡改呢?
9、CA機構與證書
你發現自己陷入了一個怪圈。數位簽章是用來進行身份認證、防止篡改以及防止否認的,數位簽章依賴公鑰的傳遞,公鑰的傳遞又需要進行身份認證以及防止篡改。。。
你把現在的設計告訴了小美,想看看她還有沒有其他的主意。
「我覺得你現在設計地已經夠好了,接下來已經不是單純的軟體設計能力能夠解決的事情了,已經上升到社會學層次的高度了。」
「這是什麼意思?」
小美解釋道:「就是說,我們應該成立類似於公證處這樣的專業機構,來認證公鑰的合法性,叫做CA。認證機構也要生成自己的一組金鑰對,分成公鑰和私鑰,私鑰自己保管,公鑰任何人都可知。」
「那這怎麼進行認證呢?」
「還是用你數位簽章的思路,比如我在分發我的公鑰讓你知道之前,我先把公鑰發給認證機構,然後認證機構用自己的私鑰對我的公鑰新增數位簽章,最後頒發一個包含我的公鑰和認證機構數位簽章的證書。這個證書就證明我的公鑰是合法的。」小美補充道,然後畫了個圖。
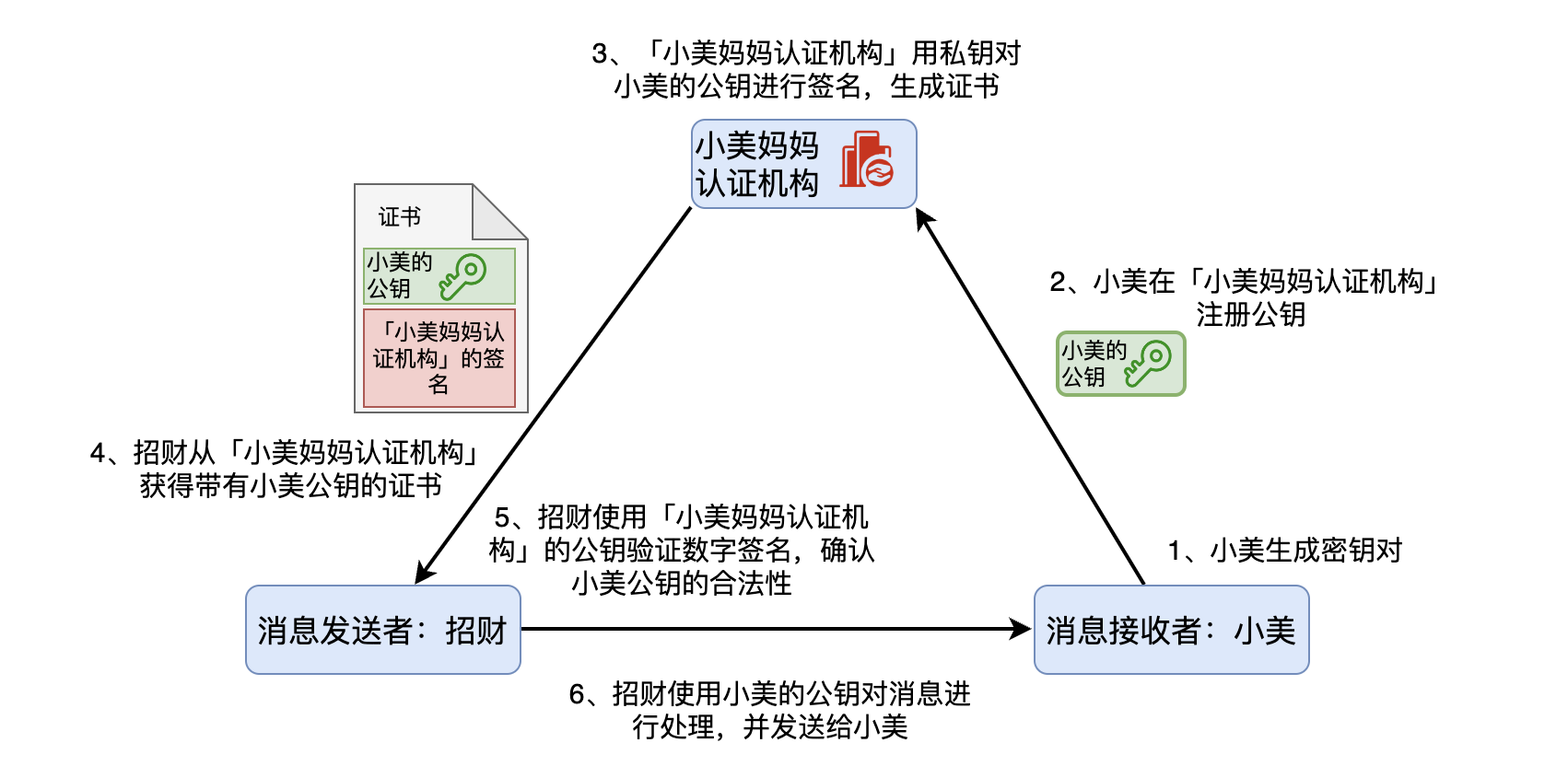
你一眼就看出了這個邏輯的漏洞,這個方案沒有從根本上解決問題,只是把問題轉移了而已。因為小美媽媽這個認證機構需要對小美的公鑰施加數位簽章,你勢必需要用到小美媽媽這個認證機構的公鑰。
「我現在不信任你的公鑰,也對你媽媽這個認證機構的公鑰有所懷疑,那認證機構對頒發的證書就沒有任何意義!依舊是個死迴圈!「你對小美提出了自己的疑問。
」那取決於你怎麼理解『信任』這個詞兒了,如果你除了自己誰也不信,那對你來說永遠不會有安全的通訊,這個邏輯鏈條就是個死迴圈。實際上,『信任』這個詞兒是比較出來的,在多個供選擇的信任物件中只要有一個你最信任的就可以了「。
小美繼續說:」我舉個例子。你覺得銀行願意把錢借給你是因為信任你這個人本身嗎?當然不是,銀行相信的是你背後抵押的房子等所有值錢的東西。回到這個例子裡,如果我媽媽的認證機構經過層層關係,最終找到了你媽媽的認證機構,你看看這個邏輯是不是就解釋的通了。「
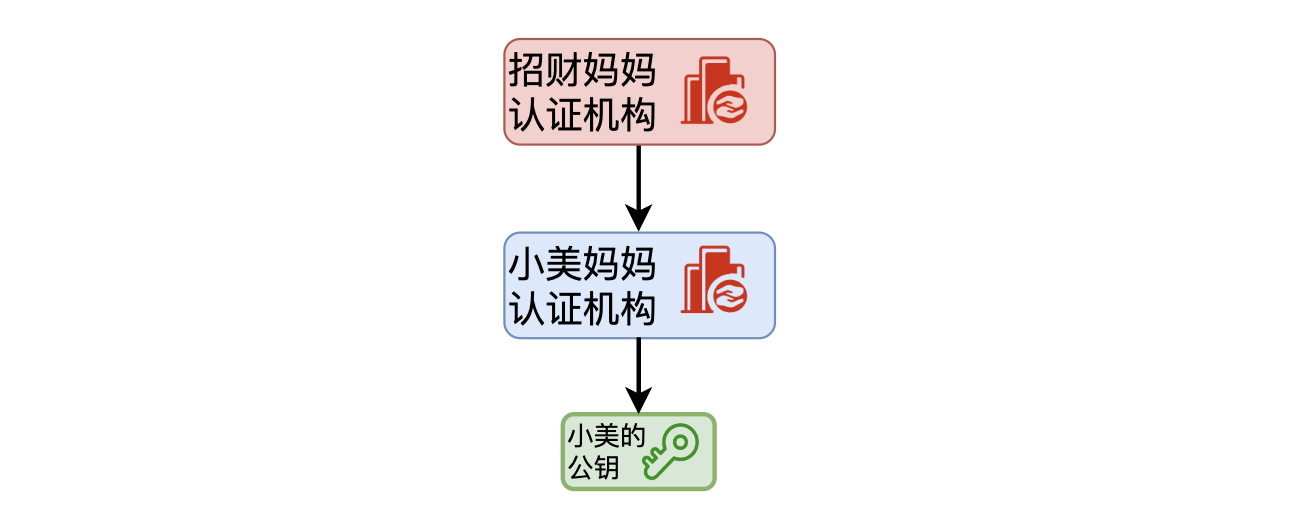
你看了一下這個層級,既然是你媽媽開的認證機構,你肯定選擇信任,由於「招財媽媽認證機構」出具了「小美媽媽認證機構」公鑰的證書,「小美媽媽認證機構」又出具了小美公鑰的證書,根據這個信任鏈條,你自然就信任小美的公鑰的合法性了。
到此,問題全部解決。
作者:蟬沐風,公眾號:蟬沐風的碼場