視覺化學習：CSS transform與仿射變換

引言

在幾年前，我就在一些部落格中看到關於CSS中transform的分析，講到它與線性代數中矩陣的關係，但當時由於使用transform比較少，再加上我畢竟是個數學學渣，對數學有點畏難心理，就有點看不下去，所以只是隨便掃了兩眼，就沒有再繼續瞭解了。現在在學習視覺化，又遇到了這個點，又說到這是視覺化的基礎知識，既然這樣，那看來還是逃不過去，那就再多瞭解一點吧。

transform的作用

使用過transform的前端小夥伴一定不陌生，通過對CSS中transform屬性的設定，我們可以對DOM元素進行縮放、旋轉、平移，以及扭曲，從而改變元素的位置、形狀、大小和角度。

仿射變換

CSS中的transform對應到圖學中的概念就是仿射變換。

仿射變換簡單來說就是「線性變換 + 平移」。

在CSS中對某個DOM元素應用仿射變換，可以簡單理解成是把這個元素原本的整個座標系進行了變換，並且這個座標系的原點在最初始時位於DOM元素的中心，X軸朝右、Y軸朝上、Z軸朝外，也就是朝向螢幕。

所以就是說，對某個DOM元素進行仿射變換，就相當於對它所對應的幾何圖形的每個頂點向量進行仿射變換。

關於圖形的仿射變換，有兩個性質：

第一，仿射變換不改變直線段的形狀，也就是說，應用仿射變換後，直線段依舊是直線段；

第二，應用相同的仿射變換後，兩條直線段的長度比例保持不變。

平移

接下來我們先說平移，平移變換是最簡單的仿射變換。

假設存在一個向量P(x0, y0)，我們想要把它沿著另一個向量Q(x1, y1)的方向移動對應距離，那隻要將兩個向量相加，我們就可以得到這個新的向量它的座標。

x = x0 + x1
y = y0 + y1

這就是平移變換的公式。

線性變換

根據公式可以看出，應用平移變換後，原始座標系的原點會發生變化。

但是應用線性變換後，原點卻並不會變化；下面來講解兩個常用的線性變換：旋轉和縮放。

• 旋轉

  首先我們先來看旋轉變換。

  

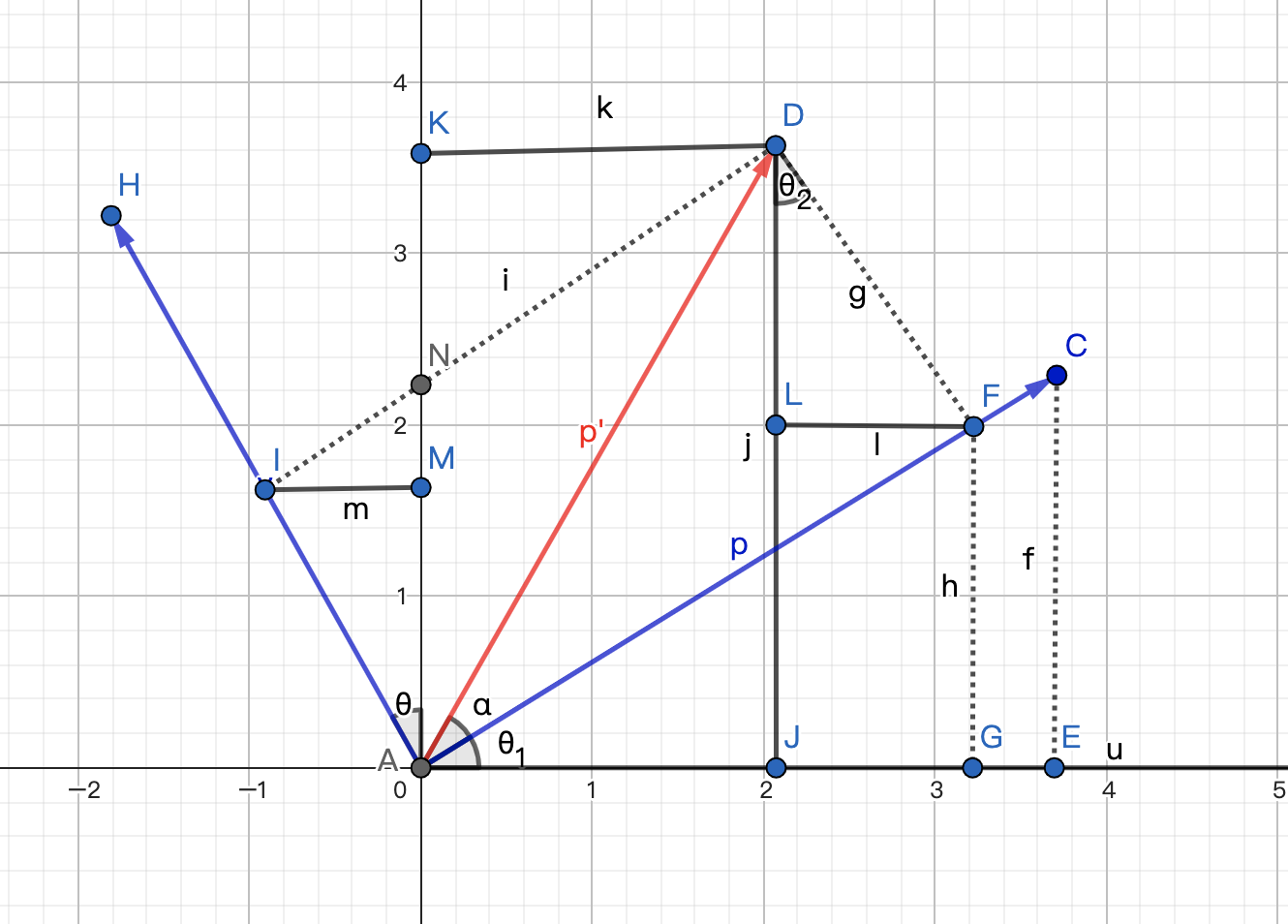
  假設存在一個向量P(x0, y0)，長度為r，與X軸夾角為θ，現在將它逆時針旋轉α角，那麼此時新的向量P'的座標x和y分別是多少呢？

  首先我們根據圓的引數方程，可以得到如下公式：

  x0 = r * cosθ
  y0 = r * sinθ
  
  x = r * cos(α+θ)
  y = r * sin(α+θ)
  

  但這樣並看不出新舊座標之間的關聯，所以需要進行推導。

  在上圖中，我們假設旋轉θ角後得到了一個新的座標系（藍色），此時我們可以求得向量P'在新座標系的座標，此時P'在新座標系的座標可以表示為：

  x' = r * cosα -> AF
  y' = r * sinα -> AI
  

  分別相當於是線段AF和AI的長度。

  此時依舊看不出新舊座標之間的關聯，我們還需要繼續推導，求出向量P'在原座標系的值，在上圖中相當於我們要求出線段AJ和AK的長度。

  • 先來求AJ的長度

    首先我們從圖中可以看出AJ = AG - JG， 並且 AG = AF * cosθ；

    同時JG 和LF的長度相同，DF與AI的長度相同，且角FDJ的度數也是θ，所以可以得到JG = AI * sinθ。

    最終我們可以得到如下公式：

    AJ = AF * cosθ - AI * sinθ 
       = r * cosα * cosθ - r * sinα * sinθ
    

    又因為：

    x0 = r * cosθ
    y0 = r * sinθ
    

    就可以得到AJ的長度，也就是新向量的x座標

    x = x0 * cosα - y0 * sinα
    

  • 接著來求AK的長度

    從圖中我們也可以看出AK = AM + MK，並且AM = AI * cosθ

    MK又可以分為MN和NK兩段，相當於MK = AF * sinθ。

    最終我們可以得到：

    AK = AI * cosθ + AF * sinθ
       = r * sinα * cosθ + r * cosα * sinθ
    

    再加上原座標和角度及半徑的關係，就可以得到AK的長度，也就是新向量的y座標：

    y = x0 * sinα + y0 * cosα
    

  至此我們就得到了新座標和原座標以及旋轉角度之間的關係，也就是旋轉變換的公式：

  x = x0 * cosα - y0 * sinα
  y = x0 * sinα + y0 * cosα
  

  根據線性代數的知識，我們可以使用矩陣的形式來表示以上公式：

  [x]   [cosα  -sinα]   [x0]
  | | = |           | x |  |
  [y]   [sinα   cosα]   [y0]
  

• 縮放

  接著我們繼續看縮放變換。縮放變換相當於是讓向量與標量相乘。

  比如我們使X軸縮放比例為sx，使Y軸縮放比例為sy，就可以得到新向量的座標為：

  x = sx * x0
  y = sy * y0
  

  縮放比旋轉簡單一些，可以直接寫出矩陣形式的公式：

  [x]   [sx  0]   [x0]
  | | = |     | x |  |
  [y]   [0  sy]   [y0]
  

至此，我們就基本瞭解了仿射變換的公式，並且可以看出線性變換的公式可以用矩陣相乘的形式進行表示。

除了不改變原點，線性變換還有另外一個性質，就是可以進行疊加；多個線性變換的疊加結果就是將線性變換的矩陣依次相乘，最後再與原始向量相乘。

根據以上內容，我們可以得到仿射變換的一般表示式：

P = M x P0 + P1

M為多個線性變換的疊加結果，也就是變換矩陣的相乘結果，P0為原始向量座標，P1為平移。

公式優化

為了便於計算，我們還可以對以上的仿射變換表示式進行優化，通過增加維度來使用矩陣進行表示：

[P]   [M  P1]   [P0]
| | = |     | x |  |
[1]   [0   1]   [1 ]

這實際上就是給線性空間增加了一個維度，用高維度的線性變換表示了低維度的仿射變換。

這種n+1維座標被稱為齊次座標，對應的矩陣被稱為齊次矩陣。

我們需要注意，由於平移變換會改變座標原點，不同的變換順序很可能會導致不同的變換結果，所以要注意矩陣相乘的順序。

公式應用

接下來我們就來應用一下線性變換的公式。

假設現在在頁面上有一個div。

<div class="block separate">我使用分開寫</div>

.block {
  width: 100px;
  height: 100px;
  color: #fff;
  background: orange;

  &.separate {
    transform: rotate(30deg) translate(100px, 50px) scale(1.5);
  }
}

通過簡單的旋轉和平移，我們改變了元素的角度、位置和大小。

此時我們對於transform的變換是分開寫的，但在CSS的transform中，可以使用一個matrix函數，讓我們對這些變換進行合併編寫。

首先我們引入一個ogl庫，使用其中定義的矩陣類Mat3（也可以藉助其他數學庫，比如mathjs）：

import { Mat3 } from 'ogl';

然後針對上面的3個變換，分別定義三個變換矩陣，分別是旋轉矩陣、平移矩陣和縮放矩陣：

const rad = Math.PI / 6;

let a = new Mat3(
    // 旋轉矩陣
    Math.cos(rad), -Math.sin(rad), 0,
    Math.sin(rad), Math.cos(rad), 0,
    0, 0, 1
);
let b = new Mat3(
    // 平移矩陣
    1, 0, 100,
    0, 1, 50,
    0, 0, 1
);
let c = new Mat3(
    // 縮放矩陣
    1.5, 0, 0,
    0, 1.5, 0,
    0, 0, 1
);

// -------------
// 使用math.js
const a = math.matrix(
  [
    [Math.cos(rad), -Math.sin(rad), 0], 
    [Math.sin(rad), Math.cos(rad), 0],
    [0, 0, 1]
  ]
);
const b = math.matrix(
  [
    [1, 0, 100], 
    [0, 1, 50],
    [0, 0, 1]
  ]
);
const c = math.matrix(
  [
    [1.5, 0, 0], 
    [0, 1.5, 0],
    [0, 0, 1]
  ]
);

接著對三個矩陣進行相乘，得到axbxc的結果：

const res = [a, b, c].reduce((prev, current) => {
  return current.multiply(prev); // prev x current 結果儲存到current
});

// -------------
// 使用math.js
let res = math.multiply(a, b);
res = math.multiply(res, c);

最後我們利用CSS變數將JS的計算結果應用到樣式上：

.block {
  // ...

  &.combine {
    --trans: none;
    transform: var(--trans);
  }
}

由於CSS的matrix是一個簡寫的齊次矩陣，它省略了三階齊次矩陣第三行的0,0,1，所以只有6個值。

const combine = document.querySelector('.combine');
const s = res.slice(0, 6);

matrix貌似是列主序，所以在設定的時候，需要按如下順序賦值：

const combine = document.querySelector('.combined');

combine.style.setProperty('--trans', `matrix(
${s[0]},${s[3]},
${s[1]},${s[4]},
${s[2]},${s[5]},
)`);


// -------------
// 使用math.js
const s = Array.from(res).map(item => item.value);
combine.style.setProperty('--trans', `matrix(
  ${s[0]},${s[3]},
  ${s[1]},${s[4]},
  ${s[2]},${s[5]}
)`);

可以明顯看出，這樣使用的效果，和rotate、translate和scale分開寫的效果是一樣的。

總結

利用仿射變換，我們可以快速繪製出形態、位置、大小各異的眾多幾何圖形，比如實現粒子動畫。

也許在普通的前端開發中，用不到太多，也並不太需要說去利用matrix去減少CSS的程式碼體積，但如果要去做視覺化方面的開發，仿射變換還是可以多去了解一下。