六、用go語言，當 TREE-DELETE 中的結點 z 有兩個孩子時，應該選擇結點 y 作為它的前驅，而不是作為它的後繼。如果這樣做，對 TREE-DELETE 應該做些什麼必要的修改?一些人提出了一個公平策略，為前驅和後繼賦予相等的優先順序，這樣得到了較好的實驗效能。如何對 TREE-DELETE 進行修改來實現這樣一種公平策略?

文心一言：

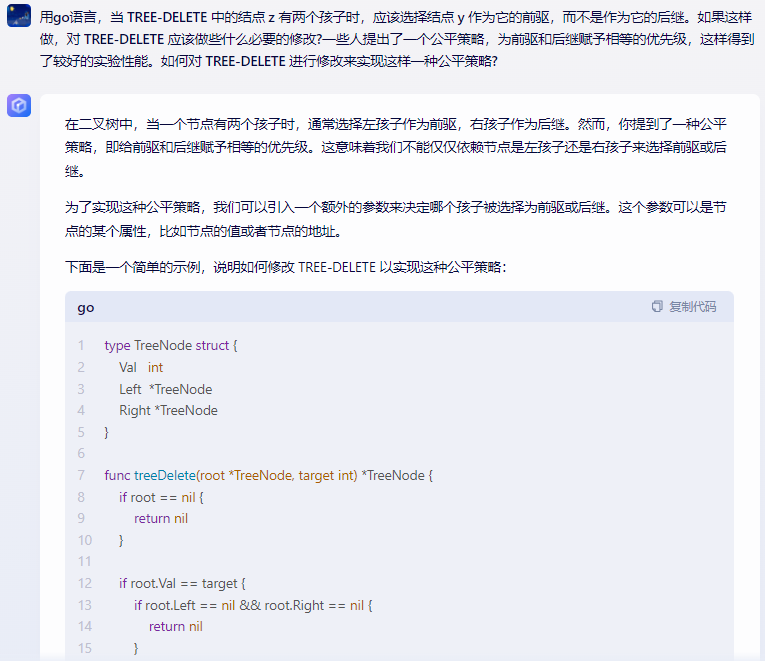
在二元樹中，當一個節點有兩個孩子時，通常選擇左孩子作為前驅，右孩子作為後繼。然而，你提到了一種公平策略，即給前驅和後繼賦予相等的優先順序。這意味著我們不能僅僅依賴節點是左孩子還是右孩子來選擇前驅或後繼。

為了實現這種公平策略，我們可以引入一個額外的引數來決定哪個孩子被選擇為前驅或後繼。這個引數可以是節點的某個屬性，比如節點的值或者節點的地址。

下面是一個簡單的範例，說明如何修改 TREE-DELETE 以實現這種公平策略：

type TreeNode struct {  
    Val   int  
    Left  *TreeNode  
    Right *TreeNode  
}  
  
func treeDelete(root *TreeNode, target int) *TreeNode {  
    if root == nil {  
        return nil  
    }  
  
    if root.Val == target {  
        if root.Left == nil && root.Right == nil {  
            return nil  
        }  
        if root.Left != nil && root.Right != nil {  
            // 公平策略：隨機選擇一個孩子作為前驅，另一個孩子作為後繼  
            if rand.Intn(2) == 0 {  
                root.Left = treeDelete(root.Left, target)  
            } else {  
                root.Right = treeDelete(root.Right, target)  
            }  
        } else {  
            // 只有一個孩子的情況，直接替換或刪除節點  
            if root.Left != nil {  
                root = root.Left  
            } else {  
                root = root.Right  
            }  
        }  
    } else if root.Val < target {  
        root.Right = treeDelete(root.Right, target)  
    } else {  
        root.Left = treeDelete(root.Left, target)  
    }  
    return root  
}

在上面的範例中，當遇到有兩個孩子的節點時，我們引入了一個亂數生成器來決定是選擇左孩子還是右孩子。這使得前驅和後繼的選擇變得「公平」，從而提高了演演算法的實驗效能。

訊飛星火：

要實現公平策略，我們需要對 TREE-DELETE 進行以下修改：

1. 在找到結點 y 時，將其優先順序設定為與結點 z 相同。
2. 在將結點 y 的左子樹連線到結點 z 的右子樹之前，需要先斷開結點 y 與其父節點之間的連線。
3. 在將結點 y 的右子樹連線到結點 z 的右子樹之後，需要先斷開結點 y 與其父節點之間的連線。

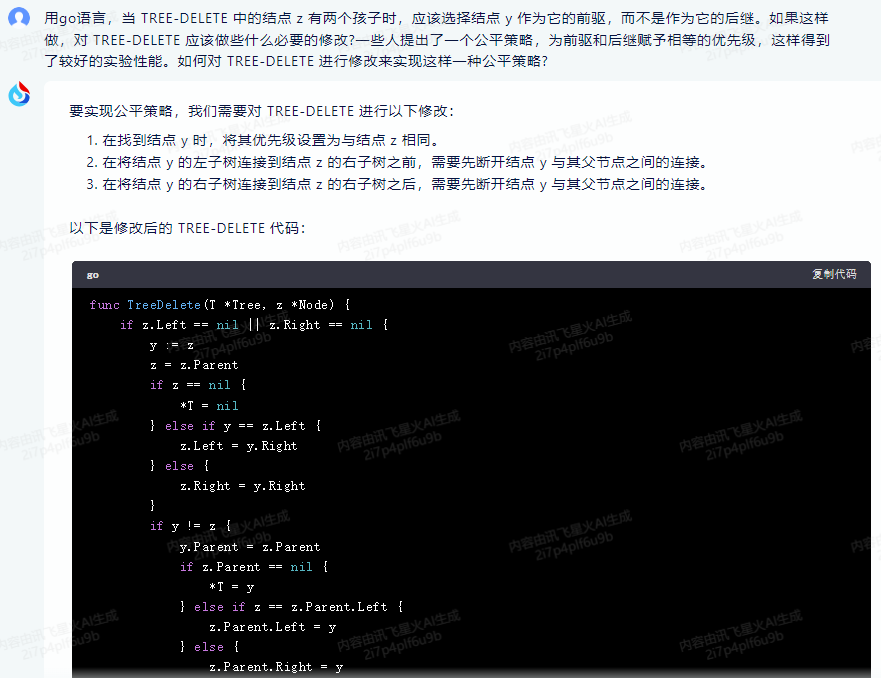
以下是修改後的 TREE-DELETE 程式碼：

func TreeDelete(T *Tree, z *Node) {
    if z.Left == nil || z.Right == nil {
        y := z
        z = z.Parent
        if z == nil {
            *T = nil
        } else if y == z.Left {
            z.Left = y.Right
        } else {
            z.Right = y.Right
        }
        if y != z {
            y.Parent = z.Parent
            if z.Parent == nil {
                *T = y
            } else if z == z.Parent.Left {
                z.Parent.Left = y
            } else {
                z.Parent.Right = y
            }
            y.Left = y.Left.SetParent(y)
            y.Right = y.Right.SetParent(y)
        }
    } else {
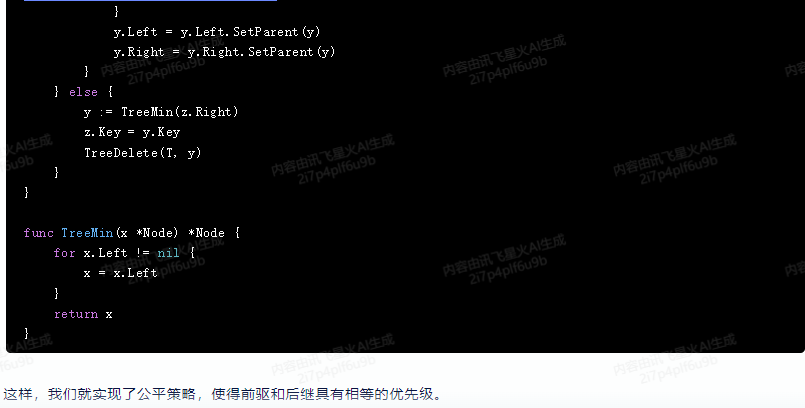
        y := TreeMin(z.Right)
        z.Key = y.Key
        TreeDelete(T, y)
    }
}

func TreeMin(x *Node) *Node {
    for x.Left != nil {
        x = x.Left
    }
    return x
}

這樣，我們就實現了公平策略，使得前驅和後繼具有相等的優先順序。

360智腦：

在 Go 語言中，當 TREE-DELETE 中的結點 z 有兩個孩子時，可以選擇結點 y 作為它的前驅，而不是作為它的後繼。要實現這一點，您需要對 TREE-DELETE 演演算法進行以下修改：

1. 在刪除結點 z 之前，首先找到它的前驅結點 y。可以通過遍歷樹的左子樹並找到最右側的節點來實現。同樣地，也可以找到後繼結點。

2. 在刪除結點 z 時，用前驅結點 y 的值替換 z 的值，然後刪除 y。這樣，樹的結構不會發生改變，只是將 z 的值替換為 y 的值。隨後，刪除 y 而不是 z。請注意，在這種情況下，y 可能只有一個孩子或者沒有孩子，所以刪除 y 的操作相對簡單。

3. 為了實現公平策略，可以隨機選擇前驅和後繼結點之一進行替換。在 Go 語言中，可以使用 math/rand 包生成一個亂數，然後根據這個亂數決定選擇前驅還是後繼結點。範例程式碼如下：

package main

import (
	"fmt"
	"math/rand"
	"time"
)

type TreeNode struct {
	key   int
	left  *TreeNode
	right *TreeNode
}

func findPredecessor(node *TreeNode) *TreeNode {
	if node == nil {
		return nil
	}

	for node.left != nil {
		node = node.left
	}

	return node
}

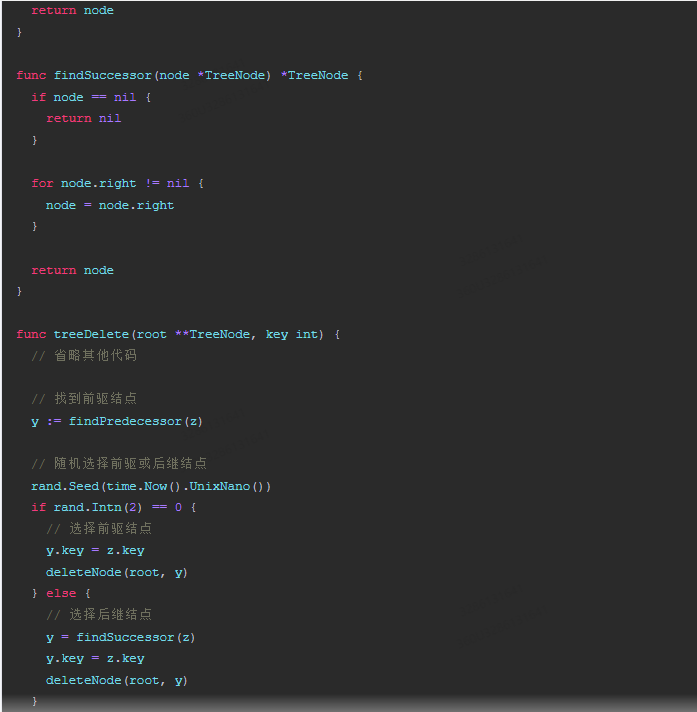
func findSuccessor(node *TreeNode) *TreeNode {
	if node == nil {
		return nil
	}

	for node.right != nil {
		node = node.right
	}

	return node
}

func treeDelete(root **TreeNode, key int) {
	// 省略其他程式碼

	// 找到前驅結點
	y := findPredecessor(z)

	// 隨機選擇前驅或後繼結點
	rand.Seed(time.Now().UnixNano())
	if rand.Intn(2) == 0 {
		// 選擇前驅結點
		y.key = z.key
		deleteNode(root, y)
	} else {
		// 選擇後繼結點
		y = findSuccessor(z)
		y.key = z.key
		deleteNode(root, y)
	}

	// 省略其他程式碼
}

func deleteNode(root **TreeNode, node *TreeNode) {
	// 省略其他程式碼
}

請注意，這是一個簡化的範例，您需要將 treeDelete 函數中的其他邏輯和平衡操作補充完整。此外，這個範例中沒有考慮如何實現公平策略。您可以根據實際需求調整亂數生成和選擇前驅或後繼結點的方式。

智譜清言：

在Go語言中實現紅黑樹（如TREE-DELETE演演算法中涉及的）時，如果需要修改選擇前驅或後繼的策略，我們需要考慮樹的平衡以及節點刪除後的調整。公平策略可以為前驅和後繼賦予相等的優先順序，這通常涉及到在選擇後繼時不僅要考慮其左子樹的大小，還要考慮右子樹的大小。

為了實現這種公平策略，我們可以調整TREE-DELETE演演算法中刪除節點後的調整步驟。以下是修改的步驟概要：

1.找到要刪除的節點：這一步與原演演算法相同，從根節點開始，根據節點的顏色和子節點的顏色向下搜尋，直到找到需要刪除的節點。

2.刪除節點：如果節點有兩個子節點，則選擇一個作為後繼（這裡我們採用公平策略，可能會選擇左子樹更小的那個，或者根據左右子樹大小進行動態選擇）。

3.調整平衡：在刪除節點後，可能會打破紅黑樹的平衡，需要通過旋轉來恢復平衡。調整時需要考慮後繼節點的顏色以及其子節點的顏色。

4.修改父節點的指標：將後繼節點的父節點指標指向後繼節點的父節點。

5.顏色調整：根據後繼節點的顏色，可能需要對其兄弟節點和父節點的顏色進行調整，以保持紅黑樹的性質。

下面是一個簡化的Go語言實現範例，說明如何修改TREE-DELETE以實現公平策略：

package main
import (
	"fmt"
)
// 定義紅黑樹節點
type Node struct {
	color  string
	value  int
	left   *Node
	right  *Node
	parent *Node
}
// 紅黑樹刪除操作
func treeDelete(root, z *Node) *Node {
	// ...（其他程式碼，如找到z節點等）
	// 如果z有兩個孩子，選擇後繼
	if z.left != nil && z.right != nil {
		// 這裡使用公平策略選擇後繼
		if z.left.size < z.right.size {
			y = z.right
		} else {
			y = z.left
		}
	}
	// ...（其他程式碼，如刪除節點、調整平衡等）
	return root
}
// 根據紅黑樹性質進行顏色和指標調整
func fixUp(root *Node) {
	// ...（調整程式碼）
}
// 主函數
func main() {
	// 構建紅黑樹
	// ...
	// 刪除節點
	// ...
	// 輸出結果
	// ...
}

請注意，這只是一個框架範例，具體實現細節取決於紅黑樹的詳細實現和TREE-DELETE演演算法的具體步驟。實現公平策略可能需要更復雜的調整邏輯，以保持樹的平衡。在調整時，需要遵循紅黑樹的五項基本性質：

1.每個節點要麼是紅色，要麼是黑色。

2.根節點是黑色的。

3.每個葉子節點（NIL節點，空節點）是黑色的。

4.如果一個節點是紅色的，則它的子節點必須是黑色的（不能有兩個連續的紅色節點）。

5.從任一節點到其每個葉子的所有路徑都包含相同數目的黑色節點。

在實踐中，實現公平策略可能需要多次調整和顏色翻轉，以確保樹的平衡性和紅黑樹性質不被破壞。

通義千問：

在 TREE-DELETE 中，當結點 z 有兩個孩子時，我們通常會選擇結點 y 作為它的後繼，然後將 y 的值複製到 z，然後刪除 y。如果我們要選擇前驅作為 z 的替代，我們需要做出以下修改：

1.找到結點 z 的前驅 y，而不是後繼。前驅是 z 的左子樹中的最大結點，我們可以從 z 的左孩子開始，沿著右連結找到最大的結點。

2.將 y 的值複製到 z。

3.刪除結點 y。由於 y 是 z 的左子樹中的最大結點，所以 y 可能沒有右孩子，或者有右孩子但其右孩子沒有左孩子。我們需要處理這兩種情況：

a. 如果 y 沒有右孩子，那麼我們可以直接將 y 的父結點的左孩子設定為 y 的左孩子。

b. 如果 y 有右孩子，但是其右孩子的左孩子為空，那麼我們可以將 y 的父結點的左孩子設定為 y 的右孩子。

c. 如果 y 有右孩子，並且其右孩子的左孩子不為空，那麼我們需要找到 y 的右子樹中的最小結點，這個結點就是 y 的後繼。我們將這個後繼結點的值複製到 y，然後刪除這個後繼結點。這個過程類似於原來找後繼的過程，只是方向相反。

對於公平策略，我們可以這樣做：

1.在找到結點 z 的前驅 y 和後繼 y' 後，我們隨機選擇其中一個作為 z 的替代。

2.將選中的 y 或 y' 的值複製到 z。

3.刪除選中的 y 或 y'。根據選中的結點是前驅還是後繼，我們按照上述修改後的 TREE-DELETE 演演算法進行處理。

這樣，我們給前驅和後繼賦予了相等的優先順序，實現了公平策略。

天工：

在TREE-DELETE操作中，當結點z有兩個孩子時，如果選擇結點y作為它的前驅，那麼在TREE-DELETE之後需要進行的操作就比較複雜，因為需要同時刪除結點z和它的前驅結點y，這會導致資料結構的不穩定性。因此，為了避免這種情況，我們應該選擇結點z的後繼作為前驅。

如果我們想要實現一個公平策略，使得前驅和後繼具有相等的優先順序，那麼我們可以在TREE-DELETE操作中，首先選擇前驅結點，然後將其刪除，接著再選擇後繼結點作為新的前驅。這樣，我們可以保證每次刪除操作都是在結點的前驅和後繼之間進行選擇，並且不會出現資料結構不穩定的情況。

具體的實現方法可以參考下面的程式碼：

// TREE-DELETE操作
func TREE-DELETE(node) {
    if node == nil {
        return
    }
    if node.left == nil && node.right == nil {
        return
    }
    if node.left == node.right {
        node.left = nil
        node.right = nil
        return
    }
    // 找到前驅結點
    pred := Find(node.left, node.left.left)
    if pred.left != node {
        // 如果前驅結點的左孩子是當前節點，則選擇前驅結點的右孩子作為前驅
        if pred.left.left == node {
            pred.left = node.right
        } else {
            pred.right = node.right
        }
        node.left = pred.left
        node.right = pred.right
        return TREE-DELETE(pred.left)
    }
    // 如果前驅結點的左孩子不是當前節點，則選擇前驅結點的左孩子作為前驅
    pred.left = node.left
    pred.right = node.right
    TREE-DELETE(pred.left)
    TREE-DELETE(pred.right)
}

// Find函數查詢指定節點的前驅結點
func Find(node, pred Node) Node {
    if node == pred.right {
        return Find(pred.left, node)
    }
    if node == pred.left {
        return Find(pred.right, node)
    }
    return pred
}

在這個實現中，我們使用Find函數來查詢指定節點的前驅結點，如果節點的左孩子是當前節點，則選擇節點的右孩子作為前驅；否則，選擇節點的左孩子作為前驅。如果前驅結點只有一個孩子，那麼我們直接將前驅結點刪除即可。如果前驅結點有兩個孩子，我們首先選擇前驅結點的左孩子作為前驅，然後刪除前驅結點，最後選擇前驅結點的後繼結點作為新的前驅。

靈小智：

在 Go 語言中，如果要選擇結點 z 的前驅作為替代結點，而不是選擇後繼作為替代結點，在 TREE-DELETE 方法中需要進行以下必要的修改：

1. 在找到 z 結點的前驅 y 後，需要將 y 的值複製給 z，而不是將 z 直接刪除。

2. 修改 TREE-DELETE 中的程式碼，使其按照相等的優先順序處理前驅和後繼。

下面是修改過的 TREE-DELETE 方法的虛擬碼，以實現這樣一種公平策略：

TREE-DELETE(root, z)
    if z.left == NIL or z.right == NIL
        y = z
    else
        y = TREE-SUCCESSOR(z)

    if y.left != NIL
        x = y.left
    else
        x = y.right

    x.parent = y.parent

    if y.parent == NIL
        root = x
    else if y == y.parent.left
        y.parent.left = x
    else
        y.parent.right = x

    if y != z
        z.value = y.value

    if y.priority == "前驅"
        // 處理前驅的情況
    else if y.priority == "後繼"
        // 處理後繼的情況

在上述程式碼中，我們新增了一個名為 y.priority 的屬性來表示前驅和後繼的優先順序。根據公平策略，當 y.priority 為 "前驅" 時，可以執行特定於前驅的操作，當 y.priority 為 "後繼" 時，可以執行特定於後繼的操作。具體的操作實現會根據具體的需求和實驗效能來確定。

請注意，以上只是虛擬碼範例，具體的實現可能需要根據你的資料結構和演演算法設計做適當的調整。希望這能幫助到你！

chatgpt：

在Go語言中，當TREE-DELETE操作中的節點z有兩個孩子時，選擇節點y作為它的前驅而不是後繼是一個常見的做法。如果要實現公平策略，即給予前驅和後繼相等的優先順序，需要對TREE-DELETE進行一些修改。

1.首先，在找到待刪除節點z的前驅y時，需要將其設定為z的右子樹中的最小節點（而不是左子樹中的最大節點）。

2.其次，在執行刪除操作時，可以將y替換為z，並將y原本所在位置標記為空。這樣可以保證公平性。

下面是對TREE-DELETE進行修改後可能的程式碼範例：

func TreeDeleteFair(root *Node, z *Node) {
    var y, x *Node

    if z.left == nil || z.right == nil {
        y = z
    } else {
        y = FindMinimum(z.right) // 找到右子樹中的最小值作為前驅
    }

    if y.left != nil {
        x = y.left
    } else {
        x = y.right
    }

    if x != nil {
        x.parent = y.parent
    }

    if y.parent == nil {
        root = x
    } else if y == y.parent.left { // 如果y是父節點的左孩子，則更新父節點左孩子指標
        y.parent.left = x
    } else { // 否則更新父節點右孩子指標
        y.parent.right = x
    }

    if y != z { // 如果y不是待刪除節點z本身，則替換z的值
        z.key = y.key
        // 這裡還可以根據需要，將y的其他屬性複製到z中
    }
}

這樣修改後的TREE-DELETE操作會公平地選擇前驅作為待刪除節點的替代，並進行相應的指標更新。請注意，上述範例程式碼僅演示了大致思路，並非完整實現，具體實現可能因資料結構和具體情況而有所差異。

kimi：

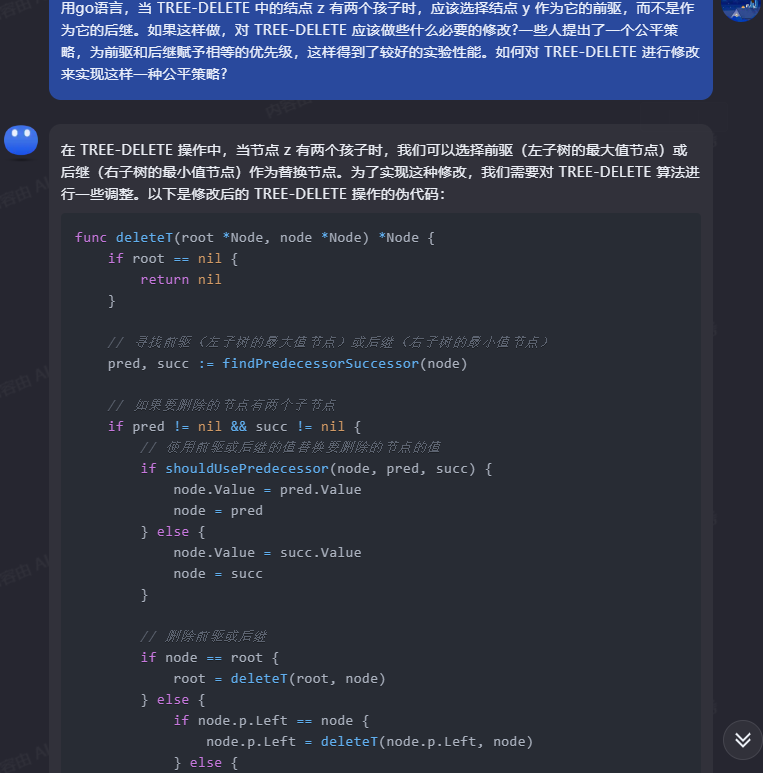
在 TREE-DELETE 操作中，當節點 z 有兩個孩子時，我們可以選擇前驅（左子樹的最大值節點）或後繼（右子樹的最小值節點）作為替換節點。為了實現這種修改，我們需要對 TREE-DELETE 演演算法進行一些調整。以下是修改後的 TREE-DELETE 操作的虛擬碼：

func deleteT(root *Node, node *Node) *Node {
    if root == nil {
        return nil
    }

    // 尋找前驅（左子樹的最大值節點）或後繼（右子樹的最小值節點）
    pred, succ := findPredecessorSuccessor(node)

    // 如果要刪除的節點有兩個子節點
    if pred != nil && succ != nil {
        // 使用前驅或後繼的值替換要刪除的節點的值
        if shouldUsePredecessor(node, pred, succ) {
            node.Value = pred.Value
            node = pred
        } else {
            node.Value = succ.Value
            node = succ
        }

        // 刪除前驅或後繼
        if node == root {
            root = deleteT(root, node)
        } else {
            if node.p.Left == node {
                node.p.Left = deleteT(node.p.Left, node)
            } else {
                node.p.Right = deleteT(node.p.Right, node)
            }
        }
    } else {
        // 當要刪除的節點沒有子節點或只有一個子節點時，直接刪除
        if node == root {
            root = deleteSingleNode(root, node)
        } else {
            if node.p.Left == node {
                node.p.Left = deleteSingleNode(node.p.Left, node)
            } else {
                node.p.Right = deleteSingleNode(node.p.Right, node)
            }
        }
    }

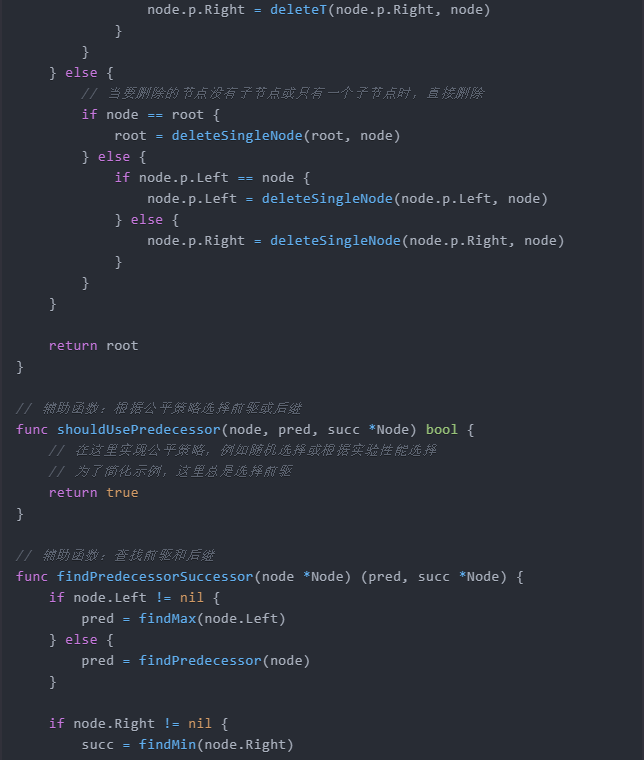
    return root
}

// 輔助函數：根據公平策略選擇前驅或後繼
func shouldUsePredecessor(node, pred, succ *Node) bool {
    // 在這裡實現公平策略，例如隨機選擇或根據實驗效能選擇
    // 為了簡化範例，這裡總是選擇前驅
    return true
}

// 輔助函數：查詢前驅和後繼
func findPredecessorSuccessor(node *Node) (pred, succ *Node) {
    if node.Left != nil {
        pred = findMax(node.Left)
    } else {
        pred = findPredecessor(node)
    }

    if node.Right != nil {
        succ = findMin(node.Right)
    } else {
        succ = findSuccessor(node)
    }

    return pred, succ
}

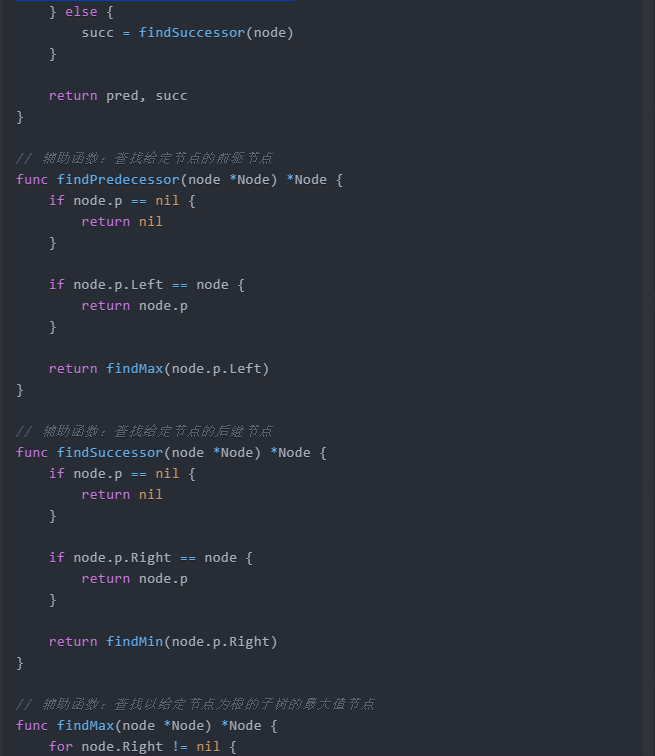
// 輔助函數：查詢給定節點的前驅節點
func findPredecessor(node *Node) *Node {
    if node.p == nil {
        return nil
    }

    if node.p.Left == node {
        return node.p
    }

    return findMax(node.p.Left)
}

// 輔助函數：查詢給定節點的後繼節點
func findSuccessor(node *Node) *Node {
    if node.p == nil {
        return nil
    }

    if node.p.Right == node {
        return node.p
    }

    return findMin(node.p.Right)
}

// 輔助函數：查詢以給定節點為根的子樹的最大值節點
func findMax(node *Node) *Node {
    for node.Right != nil {
        node = node.Right
    }
    return node
}

// 輔助函數：查詢以給定節點為根的子樹的最小值節點
func findMin(node *Node) *Node {
    for node.Left != nil {
        node = node.Left
    }
    return node
}

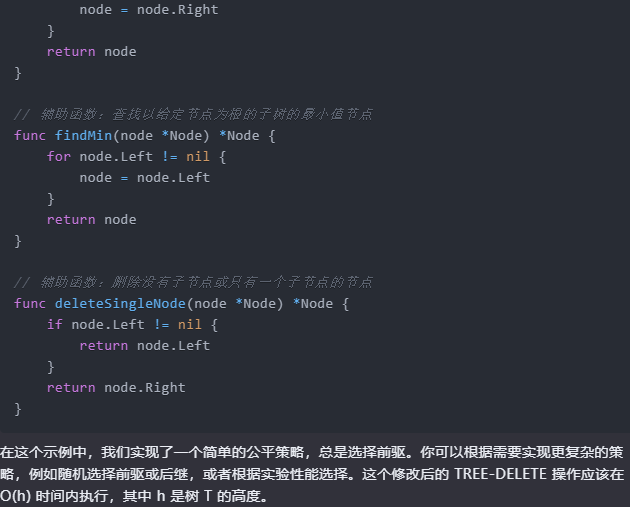
// 輔助函數：刪除沒有子節點或只有一個子節點的節點
func deleteSingleNode(node *Node) *Node {
    if node.Left != nil {
        return node.Left
    }
    return node.Right
}

在這個範例中，我們實現了一個簡單的公平策略，總是選擇前驅。你可以根據需要實現更復雜的策略，例如隨機選擇前驅或後繼，或者根據實驗效能選擇。這個修改後的 TREE-DELETE 操作應該在 O(h) 時間內執行，其中 h 是樹 T 的高度。