雙二面角耦合力場項的計算
2023-12-05 21:00:31
技術背景
當我們使用分子力場進行分子動力學模擬時，通常包括成鍵相互作用（鍵長項、鍵角項和二面角項）和非成鍵相互作用（範德華力）。而其中成鍵相互作用，可以根據作用的範圍，進一步定義成1-2相互作用、1-3相互作用和1-4相互作用，也就是鍵長鍵角和二面角。在FF19SB力場中，為了進一步提升力場模擬的精確度，引入了一個CMAP引數，用於計算\(C_{\alpha}\)位置上的二面角耦合相互作用，也可以理解為1-5相互作用，作為力場的一個修正項。這裡我們介紹具體的雙二面角耦合勢能項的計算方法。
輸入與輸出
具體的雙二面角耦合相互作用，可以參考如下圖示（圖片擷取自參考文獻1）：
力場項的輸入是\(C_{\alpha}\)周邊的兩個二面角：\(\phi\)和\(\psi\)，而我們需要計算的是這兩個引數對應的一個勢能修正項：\(E_{mod}=E(\phi,\psi)\)。根據實驗資料和量化計算出來的資料，Amber中給出了每一個氨基酸種類的二面角格點勢能：
CMAP
%FLAG CMAP_COUNT 1
%FLAG CMAP_TITLE
Gly CMAP
%FLAG CMAP_RESLIST 1
GLY
%FLAG CMAP_RESOLUTION 24
%FLAG CMAP_PARAMETER
0.82366 1.09817 1.13106 1.38658 2.11377 3.63194 5.20835 4.52792
4.24857 3.42100 2.57125 2.21561 4.26659 2.21561 2.57125 3.42110
4.24858 4.52792 4.29107 3.63184 2.03731 1.32036 1.12797 1.09814
1.01976 0.89767 0.89484 1.21525 1.97095 3.70570 4.38855 4.65256
4.43948 3.89754 4.21954 2.92219 1.83300 1.61528 2.13407 3.13273
4.03304 4.37836 4.21500 3.54162 2.14871 1.44646 1.20387 1.08264
0.94294 0.79652 0.83328 1.24136 2.06053 3.43883 4.17385 4.53101
4.43115 4.03641 3.71837 2.02965 1.28863 1.21833 1.89263 2.85593
4.80291 4.23497 4.08718 3.49858 2.17811 1.53114 1.22608 1.06909
1.06124 0.90425 0.95129 1.35925 1.80900 3.18916 3.85055 4.27470
4.17515 3.68355 2.71193 1.96823 0.88051 1.02084 1.59189 2.52883
3.47767 4.03244 3.86779 3.39508 2.23969 1.66969 1.33019 1.16679
1.08157 1.02005 1.10493 1.29605 1.79270 2.88632 3.63402 4.05349
3.97657 3.35415 2.24207 1.18576 0.74267 0.67495 1.31122 2.24278
3.21905 3.69186 4.76949 4.00571 2.34764 1.77622 1.34849 1.12849
1.09360 0.76295 0.64220 1.00733 1.73708 2.50787 3.41571 4.45847
3.84910 3.11193 1.97839 1.18177 0.33803 0.43176 1.23577 2.17947
2.92428 3.38497 3.39138 3.10177 3.35228 2.15282 1.45287 1.28536
0.61764 0.23640 0.15650 0.65857 1.56522 2.44967 3.17669 3.78043
4.22216 2.79953 1.66579 0.59084 0.15579 0.43594 1.52040 2.27449
2.76979 3.16911 3.12455 2.92674 2.45824 1.88927 1.36443 0.95121
-0.00243 -0.14438 0.06931 0.84132 1.89921 2.91978 3.46170 3.60722
3.77366 2.18724 1.52870 0.20777 0.22187 1.10049 2.08960 2.88893
3.46272 3.66327 3.40280 3.02172 2.23074 1.32476 0.62376 0.25154
-0.24862 0.05886 0.73935 1.98217 3.25167 4.06285 4.21447 3.90130
2.90300 1.70374 0.74057 0.52755 1.12943 2.10802 2.78056 3.65981
4.30377 4.58476 4.35318 3.65296 2.33204 0.81283 0.00000 -0.29835
0.44379 1.32981 2.39709 3.82578 5.02459 5.42450 4.99639 4.00610
2.64886 1.63847 1.37610 1.71448 2.28503 2.64949 3.24747 4.17266
5.17265 5.75041 5.58476 4.21912 2.20540 0.64843 0.02065 -0.08593
2.15530 3.40478 4.51993 5.80241 6.12627 6.00746 5.12631 4.58197
2.80154 2.55737 2.87599 2.95502 2.71629 2.60279 3.64721 4.53964
5.90407 6.82108 6.15044 4.18011 2.15201 0.96807 0.81255 1.19704
4.21011 5.19583 5.45356 5.26216 5.22957 4.91772 4.44698 3.93537
3.74038 4.11322 3.92595 2.94210 2.11295 2.42266 3.12536 4.83315
6.43292 6.19670 5.13463 3.65052 2.40663 2.07125 2.29840 3.03351
5.33877 4.55338 3.87255 3.87071 3.62149 3.87069 4.31250 4.77933
5.37137 5.20874 3.65026 2.18763 2.20027 2.18700 3.65026 5.21405
5.24065 4.77943 4.31250 3.87553 3.63325 5.19982 3.88530 4.53465
4.20747 3.02450 2.29840 2.07135 2.40664 3.65062 5.13204 6.19680
6.43292 4.83351 3.12587 2.96667 2.11029 2.93241 3.92594 4.11322
3.74082 3.93551 4.44698 4.92068 5.53058 5.24416 5.35209 5.19605
2.15668 1.19704 0.81255 0.96806 2.15211 4.17062 6.15034 6.82108
5.90407 4.54177 3.63728 2.60267 2.71853 2.95502 2.87589 2.55737
2.80717 3.89294 5.12631 6.00746 6.12372 5.80230 5.01898 3.40679
0.45450 -0.08700 0.02065 0.64843 2.20540 4.21912 5.58476 5.75041
5.17265 4.16788 3.24747 2.64460 2.28503 1.72593 1.37610 1.63847
2.64538 4.01006 5.00425 5.42091 5.02459 3.80593 2.39681 1.32981
-0.24862 -0.29835 0.00000 0.81283 2.33214 3.64847 4.35318 4.59008
4.30377 3.65991 2.78056 2.10802 1.84494 0.52754 0.74067 1.61716
2.90300 3.89516 4.21447 4.06285 3.25166 1.98217 0.73946 0.07427
-0.00243 0.25154 0.64043 1.82987 2.23143 3.02038 3.40280 3.66327
3.46272 2.88893 2.08960 1.10049 0.22171 0.20862 1.52897 2.18595
3.24376 3.60722 3.46170 2.91968 1.89590 0.84888 0.07066 -0.14460
0.61764 0.94007 1.36444 1.88927 2.45691 2.92674 3.12469 3.16911
2.76979 2.27377 1.52040 0.44049 0.15579 0.59084 1.66579 2.79477
4.25589 3.78043 3.17669 2.45043 1.56512 0.65855 0.15650 0.23719
1.09360 1.28549 1.45287 2.15281 2.67683 3.10177 3.39138 3.38497
2.91731 2.17947 1.23582 0.43170 0.33793 1.00844 1.97383 3.11193
3.84910 4.46392 3.41571 2.50787 1.73708 1.00733 0.64220 0.76295
0.97094 1.11640 1.33640 1.77623 2.30465 3.21763 3.71128 3.69186
3.21905 2.24277 1.31122 0.67238 0.74272 1.18578 2.24207 3.35415
3.97657 4.05349 3.63266 2.88632 1.79270 1.23680 1.00391 1.05657
0.98044 1.16708 1.33038 1.66969 2.23969 3.39508 3.86779 4.03243
3.47590 2.52883 1.59193 1.02084 0.88051 1.46518 2.71203 3.68355
4.17470 4.27471 3.85203 3.18916 1.80900 1.35925 0.95109 0.90998
0.92229 1.06909 1.22608 1.53114 2.17810 3.49858 4.08708 4.23358
3.81032 2.85593 1.89254 1.21833 1.28863 2.03059 3.37664 4.03661
4.43079 4.53101 4.17385 3.43883 2.06053 1.24136 0.83440 0.79652
1.01976 1.08264 1.20394 1.44647 2.14870 3.54162 4.22527 4.37836
4.03304 3.13273 2.13407 1.61528 1.83300 2.92219 4.10899 3.89754
4.43948 4.65256 4.38856 3.70570 1.97095 1.21515 0.89442 0.89767
這裡是一個24*24大小的Resolution表格，對應的是在空間中將兩個二面角的大小劃分成24份，每份為15度，而這裡的值給出的是每一個離散的二面角組合的勢能值。拿到這個表之後，我們需要對它做一個連續化處理，也就是使用所謂的插值法，這裡選用的是三次樣條插值。
三次樣條插值
三次樣條插值演演算法的原理還是比較簡單粗暴的，直接根據通用公式\(f(x)=ax^3+bx^2+cx+d\)進行計算，那麼就要求至少有四個輸入輸出值\(x_1,y_1,x_2,y_2,x_3,y_3,x_4,y_4\)用於插值：
\[\left(\begin{matrix}
x_1^3&&x_1^2&&x_1&&1\\
x_2^3&&x_2^2&&x_2&&1\\
x_3^3&&x_3^2&&x_3&&1\\
x_4^3&&x_4^2&&x_4&&1
\end{matrix}\right)\left(
\begin{matrix}
a\\b\\c\\d
\end{matrix}
\right)=\left(
\begin{matrix}
y_1\\y_2\\y_3\\y_4
\end{matrix}
\right)
\]
這樣就可以通過計算矩陣的逆來得到一組插值引數：
\[\left(
\begin{matrix}
a\\b\\c\\d
\end{matrix}
\right)=
\left(\begin{matrix}
x_1^3&&x_1^2&&x_1&&1\\
x_2^3&&x_2^2&&x_2&&1\\
x_3^3&&x_3^2&&x_3&&1\\
x_4^3&&x_4^2&&x_4&&1
\end{matrix}\right)^{-1}\left(
\begin{matrix}
y_1\\y_2\\y_3\\y_4
\end{matrix}
\right)
\]
如此一來我們就把一組離散的資料插值成一個可以求導的連續函數：
\[f(x)=ax^3+bx^2+cx+d\\
\frac{df}{dx}=3ax^2+2bx+c
\]
雙三次插值
回到雙二面角耦合相互租用的場景，我們按照15度一個點，對整個二面角的自變數空間做了一個離散化，可以先用視覺化的形式看一下對應的能量分佈。
import numpy as np
import matplotlib.pyplot as plt
string = """
0.82366 1.09817 1.13106 1.38658 2.11377 3.63194 5.20835 4.52792
4.24857 3.42100 2.57125 2.21561 4.26659 2.21561 2.57125 3.42110
4.24858 4.52792 4.29107 3.63184 2.03731 1.32036 1.12797 1.09814
1.01976 0.89767 0.89484 1.21525 1.97095 3.70570 4.38855 4.65256
4.43948 3.89754 4.21954 2.92219 1.83300 1.61528 2.13407 3.13273
4.03304 4.37836 4.21500 3.54162 2.14871 1.44646 1.20387 1.08264
0.94294 0.79652 0.83328 1.24136 2.06053 3.43883 4.17385 4.53101
4.43115 4.03641 3.71837 2.02965 1.28863 1.21833 1.89263 2.85593
4.80291 4.23497 4.08718 3.49858 2.17811 1.53114 1.22608 1.06909
1.06124 0.90425 0.95129 1.35925 1.80900 3.18916 3.85055 4.27470
4.17515 3.68355 2.71193 1.96823 0.88051 1.02084 1.59189 2.52883
3.47767 4.03244 3.86779 3.39508 2.23969 1.66969 1.33019 1.16679
1.08157 1.02005 1.10493 1.29605 1.79270 2.88632 3.63402 4.05349
3.97657 3.35415 2.24207 1.18576 0.74267 0.67495 1.31122 2.24278
3.21905 3.69186 4.76949 4.00571 2.34764 1.77622 1.34849 1.12849
1.09360 0.76295 0.64220 1.00733 1.73708 2.50787 3.41571 4.45847
3.84910 3.11193 1.97839 1.18177 0.33803 0.43176 1.23577 2.17947
2.92428 3.38497 3.39138 3.10177 3.35228 2.15282 1.45287 1.28536
0.61764 0.23640 0.15650 0.65857 1.56522 2.44967 3.17669 3.78043
4.22216 2.79953 1.66579 0.59084 0.15579 0.43594 1.52040 2.27449
2.76979 3.16911 3.12455 2.92674 2.45824 1.88927 1.36443 0.95121
-0.00243 -0.14438 0.06931 0.84132 1.89921 2.91978 3.46170 3.60722
3.77366 2.18724 1.52870 0.20777 0.22187 1.10049 2.08960 2.88893
3.46272 3.66327 3.40280 3.02172 2.23074 1.32476 0.62376 0.25154
-0.24862 0.05886 0.73935 1.98217 3.25167 4.06285 4.21447 3.90130
2.90300 1.70374 0.74057 0.52755 1.12943 2.10802 2.78056 3.65981
4.30377 4.58476 4.35318 3.65296 2.33204 0.81283 0.00000 -0.29835
0.44379 1.32981 2.39709 3.82578 5.02459 5.42450 4.99639 4.00610
2.64886 1.63847 1.37610 1.71448 2.28503 2.64949 3.24747 4.17266
5.17265 5.75041 5.58476 4.21912 2.20540 0.64843 0.02065 -0.08593
2.15530 3.40478 4.51993 5.80241 6.12627 6.00746 5.12631 4.58197
2.80154 2.55737 2.87599 2.95502 2.71629 2.60279 3.64721 4.53964
5.90407 6.82108 6.15044 4.18011 2.15201 0.96807 0.81255 1.19704
4.21011 5.19583 5.45356 5.26216 5.22957 4.91772 4.44698 3.93537
3.74038 4.11322 3.92595 2.94210 2.11295 2.42266 3.12536 4.83315
6.43292 6.19670 5.13463 3.65052 2.40663 2.07125 2.29840 3.03351
5.33877 4.55338 3.87255 3.87071 3.62149 3.87069 4.31250 4.77933
5.37137 5.20874 3.65026 2.18763 2.20027 2.18700 3.65026 5.21405
5.24065 4.77943 4.31250 3.87553 3.63325 5.19982 3.88530 4.53465
4.20747 3.02450 2.29840 2.07135 2.40664 3.65062 5.13204 6.19680
6.43292 4.83351 3.12587 2.96667 2.11029 2.93241 3.92594 4.11322
3.74082 3.93551 4.44698 4.92068 5.53058 5.24416 5.35209 5.19605
2.15668 1.19704 0.81255 0.96806 2.15211 4.17062 6.15034 6.82108
5.90407 4.54177 3.63728 2.60267 2.71853 2.95502 2.87589 2.55737
2.80717 3.89294 5.12631 6.00746 6.12372 5.80230 5.01898 3.40679
0.45450 -0.08700 0.02065 0.64843 2.20540 4.21912 5.58476 5.75041
5.17265 4.16788 3.24747 2.64460 2.28503 1.72593 1.37610 1.63847
2.64538 4.01006 5.00425 5.42091 5.02459 3.80593 2.39681 1.32981
-0.24862 -0.29835 0.00000 0.81283 2.33214 3.64847 4.35318 4.59008
4.30377 3.65991 2.78056 2.10802 1.84494 0.52754 0.74067 1.61716
2.90300 3.89516 4.21447 4.06285 3.25166 1.98217 0.73946 0.07427
-0.00243 0.25154 0.64043 1.82987 2.23143 3.02038 3.40280 3.66327
3.46272 2.88893 2.08960 1.10049 0.22171 0.20862 1.52897 2.18595
3.24376 3.60722 3.46170 2.91968 1.89590 0.84888 0.07066 -0.14460
0.61764 0.94007 1.36444 1.88927 2.45691 2.92674 3.12469 3.16911
2.76979 2.27377 1.52040 0.44049 0.15579 0.59084 1.66579 2.79477
4.25589 3.78043 3.17669 2.45043 1.56512 0.65855 0.15650 0.23719
1.09360 1.28549 1.45287 2.15281 2.67683 3.10177 3.39138 3.38497
2.91731 2.17947 1.23582 0.43170 0.33793 1.00844 1.97383 3.11193
3.84910 4.46392 3.41571 2.50787 1.73708 1.00733 0.64220 0.76295
0.97094 1.11640 1.33640 1.77623 2.30465 3.21763 3.71128 3.69186
3.21905 2.24277 1.31122 0.67238 0.74272 1.18578 2.24207 3.35415
3.97657 4.05349 3.63266 2.88632 1.79270 1.23680 1.00391 1.05657
0.98044 1.16708 1.33038 1.66969 2.23969 3.39508 3.86779 4.03243
3.47590 2.52883 1.59193 1.02084 0.88051 1.46518 2.71203 3.68355
4.17470 4.27471 3.85203 3.18916 1.80900 1.35925 0.95109 0.90998
0.92229 1.06909 1.22608 1.53114 2.17810 3.49858 4.08708 4.23358
3.81032 2.85593 1.89254 1.21833 1.28863 2.03059 3.37664 4.03661
4.43079 4.53101 4.17385 3.43883 2.06053 1.24136 0.83440 0.79652
1.01976 1.08264 1.20394 1.44647 2.14870 3.54162 4.22527 4.37836
4.03304 3.13273 2.13407 1.61528 1.83300 2.92219 4.10899 3.89754
4.43948 4.65256 4.38856 3.70570 1.97095 1.21515 0.89442 0.89767
"""
phi = np.arange(24) * 15
psi = np.arange(24) * 15
resolutions = np.array([float(s) for s in string.split()], np.float32).reshape((24, 24))
plt.figure(figsize=(10, 10))
plt.title('GLY Resolutions')
plt.contourf(phi, psi, resolutions, cmap=plt.cm.hot)
plt.xlabel(r'$\phi$')
plt.ylabel(r'$\psi$')
plt.xticks(phi)
plt.yticks(psi)
plt.grid()
plt.show()
得到的結果如下圖所示：
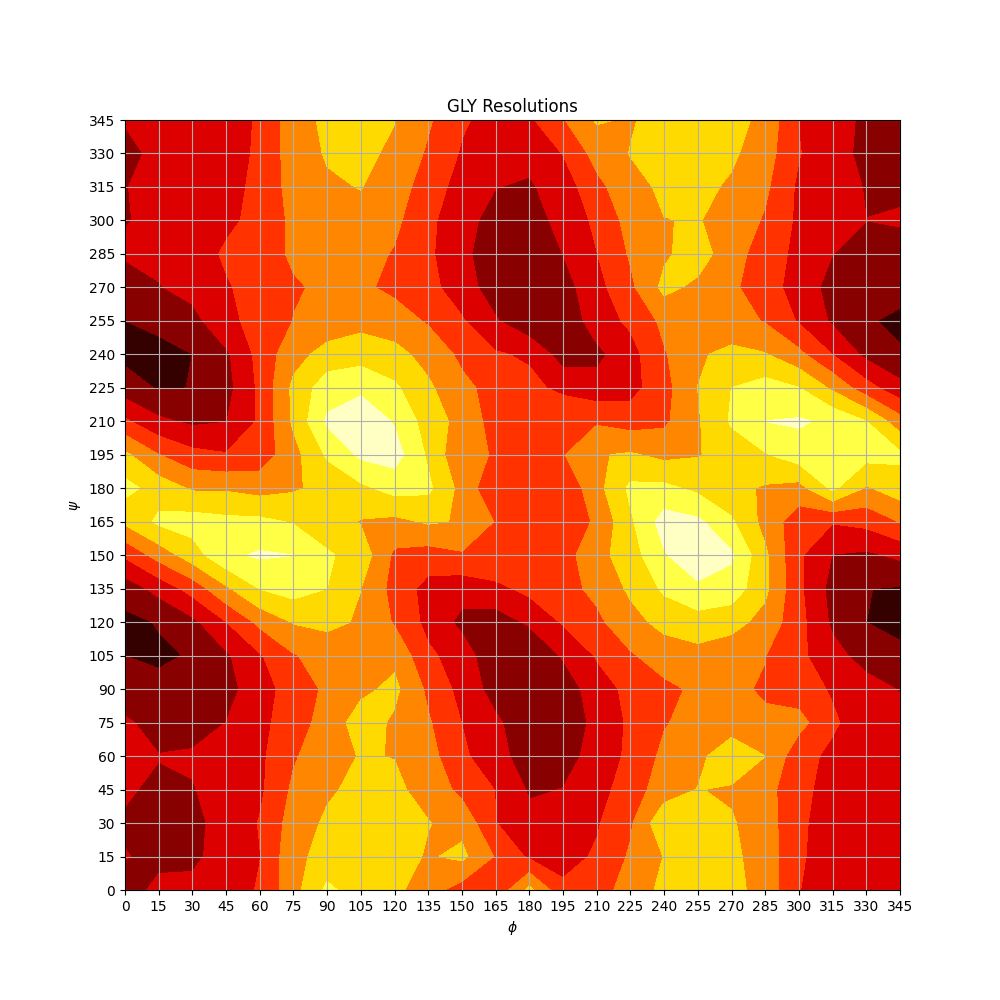
此時需要注意的是，我們手頭僅有每一個格點上的對應能量值，但是我們需要的是整個自變數空間的能量值，而且需要是連續的，這樣才能夠進行自動微分，進而求解對應的力。這時候需要用到雙三次樣條插值法。我們假設需要插值的點處在某一個方格子中間，注意不是格點了，是在某一個方格子的中間。那麼此時我們可以以這個方格的位置為中心，構造出一個九宮格。雖然是九宮格，但其實是4橫4縱一共16個能量點。這裡給出的插值目標函數為：
\[E_{interp}=\sum_{i,j=1}^4c_{i,j}\left(\frac{\phi-\phi_L}{\Delta\phi}\right)^{i-1}\left(\frac{\psi-\psi_L}{\Delta\psi}\right)^{j-1}
\]
由於係數我們是當做一維來計算的，所以需要做一個展開令\(a_{J}=a_{4i+j-4}=c_{i,j}\)，同時，我們可以將角度的變換關係全都放到係數項裡面，這樣表示\(\phi\)和\(\psi\)時在形式上就會更加簡單。經過變換後會得到一個矩陣方程：
\[\sum_{J}M_{I,J}a_J=E_I
\]
其中\(M_{I,J}\)可以通過格點的\(\phi,\psi\)與中心方格的中心點的\(\phi_L,\psi_L\)構造出來，這裡不展開寫公式，詳細內容參見程式碼實現。那麼最後得到係數矩陣\(M_{I,J}\)和能量表之後，就可以進一步得到需要插值的係數：
\[a=M^{-1}E
\]
具體的程式碼實現如下：
M = np.zeros((16, 16))
for i in range(16):
for j in range(16):
ii = i // 4
ij = i % 4
ji = j // 4
jj = j % 4
M[i][j] = (-1.5 + ij) ** ji * (-1.5 + ii) ** jj
M = np.matrix(M, np.float32)
c_0 = np.einsum('ij,j->i', M.I, E_sub.reshape(-1))
這樣就可以得到一組引數：
[ 0.80195737 -0.09009341 0.089855 0.00695395 0.00651729 0.04415806
0.00911433 -0.01563221 0.1316725 0.02541727 -0.02819001 0.01033084
0.03029101 -0.00083557 0.00954252 -0.00721776]
根據這個引數，可以代入到上面計算勢能的插值函數\( E_{interp}=\sum_{i,j=1}^4c_{i,j}\left(\frac{\phi-\phi_L}{\Delta\phi}\right)^{i-1}\left(\frac{\psi-\psi_L}{\Delta\psi}\right)^{j-1} \)中，計算出格點內給定位置的勢能值。完整的\(\phi-\psi\)空間引數計算Python程式碼如下所示：
import numpy as np
from itertools import product
import matplotlib.pyplot as plt
string = """
0.82366 1.09817 1.13106 1.38658 2.11377 3.63194 5.20835 4.52792
4.24857 3.42100 2.57125 2.21561 4.26659 2.21561 2.57125 3.42110
4.24858 4.52792 4.29107 3.63184 2.03731 1.32036 1.12797 1.09814
1.01976 0.89767 0.89484 1.21525 1.97095 3.70570 4.38855 4.65256
4.43948 3.89754 4.21954 2.92219 1.83300 1.61528 2.13407 3.13273
4.03304 4.37836 4.21500 3.54162 2.14871 1.44646 1.20387 1.08264
0.94294 0.79652 0.83328 1.24136 2.06053 3.43883 4.17385 4.53101
4.43115 4.03641 3.71837 2.02965 1.28863 1.21833 1.89263 2.85593
4.80291 4.23497 4.08718 3.49858 2.17811 1.53114 1.22608 1.06909
1.06124 0.90425 0.95129 1.35925 1.80900 3.18916 3.85055 4.27470
4.17515 3.68355 2.71193 1.96823 0.88051 1.02084 1.59189 2.52883
3.47767 4.03244 3.86779 3.39508 2.23969 1.66969 1.33019 1.16679
1.08157 1.02005 1.10493 1.29605 1.79270 2.88632 3.63402 4.05349
3.97657 3.35415 2.24207 1.18576 0.74267 0.67495 1.31122 2.24278
3.21905 3.69186 4.76949 4.00571 2.34764 1.77622 1.34849 1.12849
1.09360 0.76295 0.64220 1.00733 1.73708 2.50787 3.41571 4.45847
3.84910 3.11193 1.97839 1.18177 0.33803 0.43176 1.23577 2.17947
2.92428 3.38497 3.39138 3.10177 3.35228 2.15282 1.45287 1.28536
0.61764 0.23640 0.15650 0.65857 1.56522 2.44967 3.17669 3.78043
4.22216 2.79953 1.66579 0.59084 0.15579 0.43594 1.52040 2.27449
2.76979 3.16911 3.12455 2.92674 2.45824 1.88927 1.36443 0.95121
-0.00243 -0.14438 0.06931 0.84132 1.89921 2.91978 3.46170 3.60722
3.77366 2.18724 1.52870 0.20777 0.22187 1.10049 2.08960 2.88893
3.46272 3.66327 3.40280 3.02172 2.23074 1.32476 0.62376 0.25154
-0.24862 0.05886 0.73935 1.98217 3.25167 4.06285 4.21447 3.90130
2.90300 1.70374 0.74057 0.52755 1.12943 2.10802 2.78056 3.65981
4.30377 4.58476 4.35318 3.65296 2.33204 0.81283 0.00000 -0.29835
0.44379 1.32981 2.39709 3.82578 5.02459 5.42450 4.99639 4.00610
2.64886 1.63847 1.37610 1.71448 2.28503 2.64949 3.24747 4.17266
5.17265 5.75041 5.58476 4.21912 2.20540 0.64843 0.02065 -0.08593
2.15530 3.40478 4.51993 5.80241 6.12627 6.00746 5.12631 4.58197
2.80154 2.55737 2.87599 2.95502 2.71629 2.60279 3.64721 4.53964
5.90407 6.82108 6.15044 4.18011 2.15201 0.96807 0.81255 1.19704
4.21011 5.19583 5.45356 5.26216 5.22957 4.91772 4.44698 3.93537
3.74038 4.11322 3.92595 2.94210 2.11295 2.42266 3.12536 4.83315
6.43292 6.19670 5.13463 3.65052 2.40663 2.07125 2.29840 3.03351
5.33877 4.55338 3.87255 3.87071 3.62149 3.87069 4.31250 4.77933
5.37137 5.20874 3.65026 2.18763 2.20027 2.18700 3.65026 5.21405
5.24065 4.77943 4.31250 3.87553 3.63325 5.19982 3.88530 4.53465
4.20747 3.02450 2.29840 2.07135 2.40664 3.65062 5.13204 6.19680
6.43292 4.83351 3.12587 2.96667 2.11029 2.93241 3.92594 4.11322
3.74082 3.93551 4.44698 4.92068 5.53058 5.24416 5.35209 5.19605
2.15668 1.19704 0.81255 0.96806 2.15211 4.17062 6.15034 6.82108
5.90407 4.54177 3.63728 2.60267 2.71853 2.95502 2.87589 2.55737
2.80717 3.89294 5.12631 6.00746 6.12372 5.80230 5.01898 3.40679
0.45450 -0.08700 0.02065 0.64843 2.20540 4.21912 5.58476 5.75041
5.17265 4.16788 3.24747 2.64460 2.28503 1.72593 1.37610 1.63847
2.64538 4.01006 5.00425 5.42091 5.02459 3.80593 2.39681 1.32981
-0.24862 -0.29835 0.00000 0.81283 2.33214 3.64847 4.35318 4.59008
4.30377 3.65991 2.78056 2.10802 1.84494 0.52754 0.74067 1.61716
2.90300 3.89516 4.21447 4.06285 3.25166 1.98217 0.73946 0.07427
-0.00243 0.25154 0.64043 1.82987 2.23143 3.02038 3.40280 3.66327
3.46272 2.88893 2.08960 1.10049 0.22171 0.20862 1.52897 2.18595
3.24376 3.60722 3.46170 2.91968 1.89590 0.84888 0.07066 -0.14460
0.61764 0.94007 1.36444 1.88927 2.45691 2.92674 3.12469 3.16911
2.76979 2.27377 1.52040 0.44049 0.15579 0.59084 1.66579 2.79477
4.25589 3.78043 3.17669 2.45043 1.56512 0.65855 0.15650 0.23719
1.09360 1.28549 1.45287 2.15281 2.67683 3.10177 3.39138 3.38497
2.91731 2.17947 1.23582 0.43170 0.33793 1.00844 1.97383 3.11193
3.84910 4.46392 3.41571 2.50787 1.73708 1.00733 0.64220 0.76295
0.97094 1.11640 1.33640 1.77623 2.30465 3.21763 3.71128 3.69186
3.21905 2.24277 1.31122 0.67238 0.74272 1.18578 2.24207 3.35415
3.97657 4.05349 3.63266 2.88632 1.79270 1.23680 1.00391 1.05657
0.98044 1.16708 1.33038 1.66969 2.23969 3.39508 3.86779 4.03243
3.47590 2.52883 1.59193 1.02084 0.88051 1.46518 2.71203 3.68355
4.17470 4.27471 3.85203 3.18916 1.80900 1.35925 0.95109 0.90998
0.92229 1.06909 1.22608 1.53114 2.17810 3.49858 4.08708 4.23358
3.81032 2.85593 1.89254 1.21833 1.28863 2.03059 3.37664 4.03661
4.43079 4.53101 4.17385 3.43883 2.06053 1.24136 0.83440 0.79652
1.01976 1.08264 1.20394 1.44647 2.14870 3.54162 4.22527 4.37836
4.03304 3.13273 2.13407 1.61528 1.83300 2.92219 4.10899 3.89754
4.43948 4.65256 4.38856 3.70570 1.97095 1.21515 0.89442 0.89767
"""
def E_interp(c, phi, psi):
# 根據計算好的引數以及輸入的phi和psi值，計算勢能值
rc = c.reshape((4, 4))
E = 0
for i in range(4):
for j in range(4):
E += rc[i][j] * phi ** i * psi ** j
return E
def get_c0(E_sub):
# 計算插值引數
M = np.zeros((16, 16))
for i in range(16):
for j in range(16):
ii = i // 4
ij = i % 4
ji = j // 4
jj = j % 4
M[i][j] = (-1.5 + ii) ** ji * (-1.5 + ij) ** jj
M = np.matrix(M, np.float32)
c_0 = np.einsum('ij,j->i', M.I, E_sub.reshape(-1))
return c_0
resolutions = np.array([float(s) for s in string.split()], np.float32).reshape((24, 24))
def get_resolution_0(resolutions, phi_L=0., psi_L=0.):
# 遍歷空間中每個網格的中心，計算勢能值
Einterp = np.zeros((23, 23))
for i in range(23):
for j in range(23):
idx = list(product([i-1, i, i+1, (i+2) % 24], [j-1, j, i+1, (j+2) % 24]))
E_sub = np.array([resolutions[x] for x in idx]).reshape((4, 4))
c0 = get_c0(E_sub)
Einterp[i][j] = E_interp(c0, phi_L, psi_L)
return Einterp
phi = np.arange(23) * 15
psi = np.arange(23) * 15
hi, si = 0., 0.
# 網格中心的勢能分佈
resolutions_0 = get_resolution_0(resolutions, hi, si)
hi, si = -0.5, -0.5
# 網格格點的勢能分佈
resolutions_1 =get_resolution_0(resolutions, hi, si)
# 繪圖
plt.figure(figsize=(20, 10))
plt.subplot(1,2,1)
plt.title('GLY Resolutions Center')
plt.contourf(phi+7.5, psi+7.5, resolutions_0, cmap=plt.cm.hot)
plt.xlabel(r'$\phi$')
plt.ylabel(r'$\psi$')
plt.xticks(phi+7.5, rotation=60)
plt.yticks(psi+7.5)
plt.grid()
plt.subplot(1,2,2)
plt.title('GLY Resolutions Grid')
plt.contourf(phi, psi, resolutions_1, cmap=plt.cm.hot)
plt.xlabel(r'$\phi$')
plt.ylabel(r'$\psi$')
plt.xticks(phi, rotation=60)
plt.yticks(psi)
plt.grid()
plt.show()
輸出的結果如下所示：
Amber演演算法復現
在Amber裡面，就是直接使用雙三次樣條插值進行計算，這裡不對其演演算法進行展開介紹，但是可以貼一部分用於復現的程式碼：
def get_c1(E_sub):
dM = np.matrix([[1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[1., 0., 0., 0., 1., 0., 0., 0., 1., 0., 0., 0., 1., 0., 0., 0.],
[1., 1., 1., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 0., 0., 0., 2., 0., 0., 0., 3., 0., 0., 0.],
[0., 0., 0., 0., 1., 1., 1., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 1., 1., 1., 2., 2., 2., 2., 3., 3., 3., 3.],
[0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 1., 0., 0., 0., 1., 0., 0., 0., 1., 0., 0., 0., 1., 0., 0.],
[0., 1., 2., 3., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 1., 2., 3., 0., 1., 2., 3., 0., 1., 2., 3., 0., 1., 2., 3.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 2., 0., 0., 0., 3., 0., 0.],
[0., 0., 0., 0., 0., 1., 2., 3., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 2., 3., 0., 2., 4., 6., 0., 3., 6., 9.]],
np.float32)
dE = np.array([E_sub[1][1], E_sub[2][1], E_sub[1][2], E_sub[2][2],
0.5 * (E_sub[2][1] - E_sub[0][1]), 0.5 * (E_sub[3][1] - E_sub[1][1]),
0.5 * (E_sub[2][2] - E_sub[0][2]), 0.5 * (E_sub[3][2] - E_sub[1][2]),
0.5 * (E_sub[1][2] - E_sub[1][0]), 0.5 * (E_sub[2][2] - E_sub[2][0]),
0.5 * (E_sub[1][3] - E_sub[1][1]), 0.5 * (E_sub[2][3] - E_sub[2][1]),
0.25 * (E_sub[2][2] + E_sub[0][0] - E_sub[2][0] - E_sub[0][2]),
0.25 * (E_sub[3][2] + E_sub[1][0] - E_sub[3][0] - E_sub[1][2]),
0.25 * (E_sub[2][2] + E_sub[0][2] - E_sub[2][1] - E_sub[0][3]),
0.25 * (E_sub[3][3] + E_sub[1][1] - E_sub[3][1] - E_sub[1][3])],
np.float32)
c_1 = np.einsum('ij,j->i', dM.I, dE)
return c_1
這個雙三次樣條插值演演算法的基本原理，不是像之前我們提到的一樣使用格點中心點作為中心來進行插值，而是選取了中心網格的左上角格點作為中心(0,0)，然後對中間網格的四個格點、以及邊的一階差分、二階差分進行插值。這樣做的好處是，在網格的邊緣處，不僅僅是勢能面光滑，且一階導數可以連續。
總結概要
本文介紹了最新的一些分子力場中有可能使用到的1-5相互作用——雙二面角耦合項的計算。而常規的計算方式是，通過量化的計算得到每一個Residue的α碳對應的兩個二面角的數值在空間中的離散化數值。然後在分子模擬的過程中使用插值的方案，對相關的條目進行計算，例如使用雙三次樣條插值。但其實這種插值演演算法的使用有可能導致一些其他的問題，比如深度學習中可能會經常提到的「過擬合」問題。由於這個條目本身就只是一個修正項，從數值大小上來說並不算大，因此這些細節是否需要優化還有待商榷。
版權宣告
本文首發連結為：https://www.cnblogs.com/dechinphy/p/cmap.html
作者ID：DechinPhy
更多原著文章：https://www.cnblogs.com/dechinphy/
請博主喝咖啡：https://www.cnblogs.com/dechinphy/gallery/image/379634.html
參考文獻
- Extending the Treatment of Backbone Energetics in Protein Force Fields: Limitations of Gas-Phase Quantum Mechanics in Reproducing Protein Conformational Distributions in Molecular Dynamics Simulations.