聊聊神經網路模型流程與折積神經網路的實現
神經網路模型流程
神經網路模型的搭建流程,整理下自己的思路,這個過程不會細分出來,而是主流程。
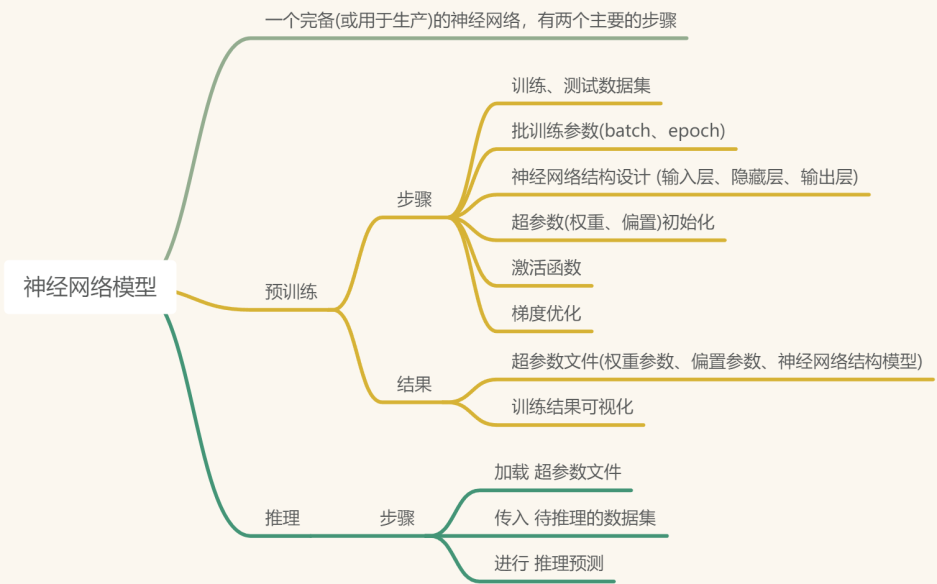
在這裡我主要是把整個流程分為兩個主流程,即預訓練與推理。預訓練過程主要是生成超引數檔案與搭設神經網路結構;而推理過程就是在應用超引數與神經網路。
折積神經網路的實現
在 聊聊折積神經網路CNN中,將折積神經的理論概述了一下,現在要大概的實踐了。整個程式碼不基於pytorch/tensorflow這類大框架,而是基於numpy庫原生來實現演演算法。pytorch/tensorflow中的運算元/函數只是由別人已實現了,我們呼叫而已;而基於numpy要自己實現一遍,雖然並不很嚴謹,但用於學習足以。
原始碼是來自《深度學習入門:基於Python的理論與實現》,可以在 https://www.ituring.com.cn/book/1921 上獲取下載
搭建CNN
網路構成如下:
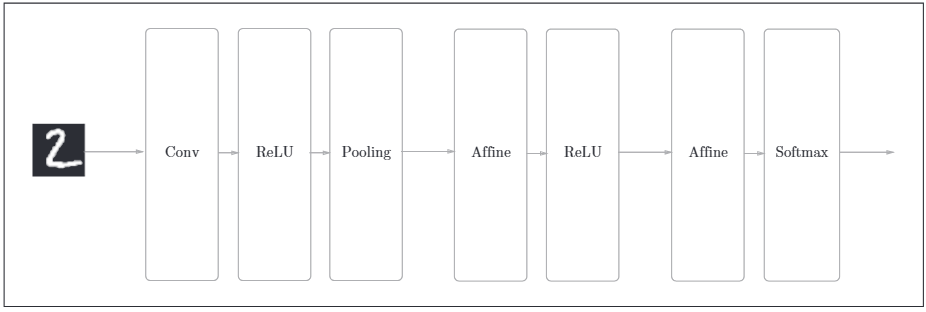
如圖所示,網路的構成是"Conv-ReLU-Pooling-Affine-ReLU-Affine-Softmax". 對於折積層與池化層的計算,由於其是四維資料(資料量,通道,高,長),不太好計算,使用im2col函數將其展開成二維 2 × 2的資料,最後輸出時,利用numpy庫的reshape函數轉換輸出的大小,方便計算。其示意圖如下:
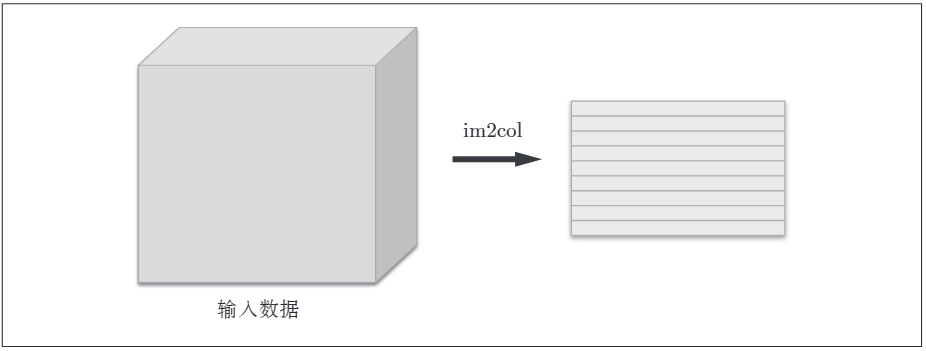
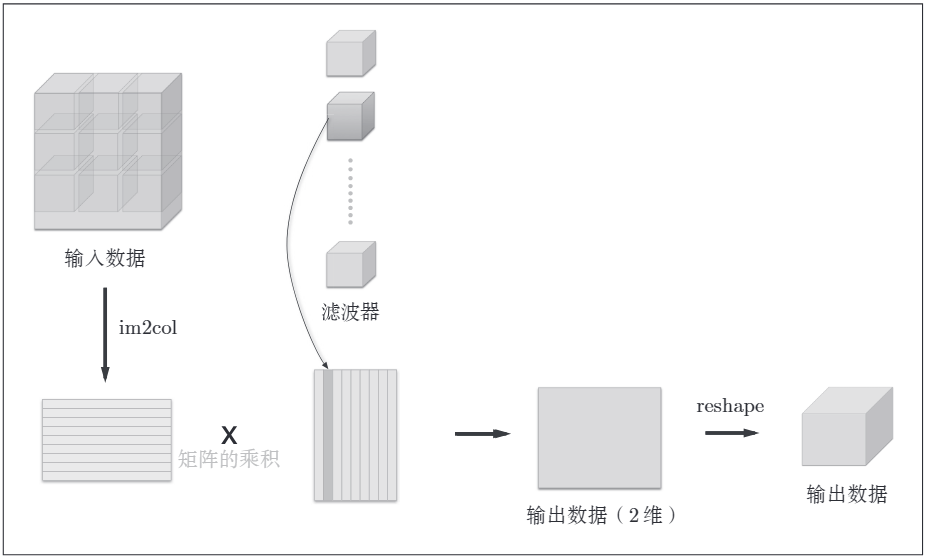
這樣也滿足了矩陣內積計算的要求,即 行列數要對應
CNN程式程式碼實現如下:
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 為了匯入父目錄的檔案而進行的設定
import pickle
import numpy as np
from collections import OrderedDict
from DeepLearn_Base.common.layers import *
from DeepLearn_Base.common.gradient import numerical_gradient
class SimpleConvNet:
"""簡單的ConvNet
conv - relu - pool - affine - relu - affine - softmax
Parameters
----------
input_dim: 輸入資料的維度,通道、高、長
conv_param: 折積核引數; filter_num:折積核數量; filter_size:折積核大小; stride:步幅; pad:填充
input_size : 輸入大小(MNIST的情況下為784)
hidden_size_list : 隱藏層的神經元數量的列表(e.g. [100, 100, 100])
output_size : 輸出大小(MNIST的情況下為10)
activation : 'relu' or 'sigmoid'
weight_init_std : 指定權重的標準差(e.g. 0.01)
指定'relu'或'he'的情況下設定「He的初始值」
指定'sigmoid'或'xavier'的情況下設定「Xavier的初始值」
"""
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
# 初始化權重
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * \
np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# 生成層
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()
# 需要處理資料,將輸入資料的多維與折積核的多維分別展平後做矩陣運算
# 在神經網路的中間層(conv,relu,pooling,affine等)的forward函數中用到了img2col與reshape結合展平資料,用向量內積運算
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
"""求損失函數
引數x是輸入資料、t是教師標籤
"""
y = self.predict(x)
return self.last_layer.forward(y, t)
# 計算精確度
def accuracy(self, x, t, batch_size=100):
if t.ndim != 1 : t = np.argmax(t, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
tt = t[i*batch_size:(i+1)*batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == tt)
return acc / x.shape[0]
def numerical_gradient(self, x, t):
"""求梯度(數值微分)
Parameters
----------
x : 輸入資料
t : 教師標籤
Returns
-------
具有各層的梯度的字典變數
grads['W1']、grads['W2']、...是各層的權重
grads['b1']、grads['b2']、...是各層的偏置
"""
loss_w = lambda w: self.loss(x, t)
grads = {}
for idx in (1, 2, 3):
grads['W' + str(idx)] = numerical_gradient(loss_w, self.params['W' + str(idx)])
grads['b' + str(idx)] = numerical_gradient(loss_w, self.params['b' + str(idx)])
return grads
def gradient(self, x, t):
"""求梯度(誤差反向傳播法)
Parameters
----------
x : 輸入資料
t : 教師標籤
Returns
-------
具有各層的梯度的字典變數
grads['W1']、grads['W2']、...是各層的權重
grads['b1']、grads['b2']、...是各層的偏置
"""
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 設定
grads = {}
grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
def save_params(self, file_name="params.pkl"):
params = {}
for key, val in self.params.items():
params[key] = val
with open(file_name, 'wb') as f:
pickle.dump(params, f)
def load_params(self, file_name="params.pkl"):
with open(file_name, 'rb') as f:
params = pickle.load(f)
for key, val in params.items():
self.params[key] = val
for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
self.layers[key].W = self.params['W' + str(i+1)]
self.layers[key].b = self.params['b' + str(i+1)]
啟用函數與折積函數的實現程式碼沒有詳細的寫出來,可以自己去下載檢視
在這整個的過程中,我個人覺得最難的就是神經網路層的搭建與資料的計算。前者決定了神經網路的結構,而後者決定了是否最終結果。通過將資料展平,才能方便,正確的進行向量內積計算。
預訓練
trainer.py檔案是進行神經網路訓練的類,會統計執行完一個epoch後的精確度,過程要選擇梯度更新演演算法,學習率,批大小,epoch次數等引數。
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 為了匯入父目錄的檔案而進行的設定
import numpy as np
from DeepLearn_Base.common.optimizer import *
class Trainer:
"""進行神經網路的訓練的類
epochs: 以所有資料走完前向、後向傳播為一次;該數值表示為總次數
mini_batch_size: 100; 每批次迭代多少資料
evaluate_sample_num_per_epoch: 1000;
"""
def __init__(self, network, x_train, t_train, x_test, t_test,
epochs=20, mini_batch_size=100,
optimizer='SGD', optimizer_param={'lr':0.01},
evaluate_sample_num_per_epoch=None, verbose=True):
self.network = network
self.verbose = verbose
self.x_train = x_train
self.t_train = t_train
self.x_test = x_test
self.t_test = t_test
self.epochs = epochs
self.batch_size = mini_batch_size
self.evaluate_sample_num_per_epoch = evaluate_sample_num_per_epoch
# optimzer: 梯度更新優化器; 更新多種梯度更新演演算法實現梯度更新.
optimizer_class_dict = {'sgd':SGD, 'momentum':Momentum, 'nesterov':Nesterov,
'adagrad':AdaGrad, 'rmsprpo':RMSprop, 'adam':Adam}
self.optimizer = optimizer_class_dict[optimizer.lower()](**optimizer_param)
self.train_size = x_train.shape[0]
self.iter_per_epoch = max(self.train_size / mini_batch_size, 1)
self.max_iter = int(epochs * self.iter_per_epoch)
self.current_iter = 0
self.current_epoch = 0
self.train_loss_list = []
self.train_acc_list = []
self.test_acc_list = []
def train_step(self):
# 隨機挑選批次的資料進行梯度更新
batch_mask = np.random.choice(self.train_size, self.batch_size)
x_batch = self.x_train[batch_mask]
t_batch = self.t_train[batch_mask]
# 開始更新梯度
grads = self.network.gradient(x_batch, t_batch)
self.optimizer.update(self.network.params, grads)
# 計算損失
loss = self.network.loss(x_batch, t_batch)
self.train_loss_list.append(loss)
if self.verbose: print("train loss:" + str(loss))
# 計算是否完成了一個epoch的執行
if self.current_iter % self.iter_per_epoch == 0:
self.current_epoch += 1
x_train_sample, t_train_sample = self.x_train, self.t_train
x_test_sample, t_test_sample = self.x_test, self.t_test
if not self.evaluate_sample_num_per_epoch is None:
t = self.evaluate_sample_num_per_epoch
x_train_sample, t_train_sample = self.x_train[:t], self.t_train[:t]
x_test_sample, t_test_sample = self.x_test[:t], self.t_test[:t]
train_acc = self.network.accuracy(x_train_sample, t_train_sample)
test_acc = self.network.accuracy(x_test_sample, t_test_sample)
self.train_acc_list.append(train_acc)
self.test_acc_list.append(test_acc)
if self.verbose: print("=== epoch:" + str(self.current_epoch) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc) + " ===")
self.current_iter += 1
def train(self):
for i in range(self.max_iter):
self.train_step()
test_acc = self.network.accuracy(self.x_test, self.t_test)
if self.verbose:
print("=============== Final Test Accuracy ===============")
print("test acc:" + str(test_acc))
在神經網路訓練中,epoch引數是指將整個訓練集通過模型一次,並更新模型引數的過程。每一次epoch,模型都會將訓練集中的所有樣本通過一次,並根據這些樣本的標籤和模型預測的結果計算損失值,然後根據損失值對模型的引數進行更新。這個過程會重複進行,直到達到預設的epoch數。
正式開始預訓練,要準備好訓練資料集,初始化CNN,梯度優化引數,超引數儲存路徑等。如下所示:
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 為了匯入父目錄的檔案而進行的設定
import numpy as np
import matplotlib.pyplot as plt
from DeepLearn_Base.dataset.mnist import load_mnist
from simple_convnet import SimpleConvNet
from DeepLearn_Base.common.trainer import Trainer
# 讀入資料
# 輸入資料的表現形式,可以是多維的,可以是展平(reshape)為一維的
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)
# 處理花費時間較長的情況下減少資料,擷取部分資料
# 訓練資料擷取 5000 條
# 測試資料擷取 1000 條
x_train, t_train = x_train[:5000], t_train[:5000]
x_test, t_test = x_test[:1000], t_test[:1000]
# 初始化epoch
max_epochs = 20
# 初始化CNN
# input_dim, 輸入資料: channel, height, width
# conv_param, 折積核引數: filter_num:折積核數量; filter_size:折積核大小; stride:步幅; pad:填充; 30個5 × 5,通道為1的折積核
network = SimpleConvNet(input_dim=(1,28,28),
conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
# 初始化預訓練
# optimizer: 梯度優化演演算法; lr表示學習率
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=max_epochs, mini_batch_size=100,
optimizer='Adam', optimizer_param={'lr': 0.001},
evaluate_sample_num_per_epoch=1000)
trainer.train()
# 儲存引數
network.save_params("E:\\workcode\\code\\DeepLearn_Base\\ch07\\cnn_params.pkl")
print("Saved Network Parameters!")
# 繪製圖形
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, trainer.train_acc_list, marker='o', label='train', markevery=2)
plt.plot(x, trainer.test_acc_list, marker='s', label='test', markevery=2)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
預訓練好後,檢視是否生成超引數檔案。
推理
準備好測試資料集,應用已預訓練好的神經網路模型與超引數。
# coding: utf-8
import sys, os
# 為了匯入父目錄的檔案而進行的設定
sys.path.append(os.pardir)
import numpy as np
from DeepLearn_Base.dataset.mnist import load_mnist
from DeepLearn_Base.common.functions import sigmoid, softmax
from simple_convnet import SimpleConvNet
def get_data():
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)
return x_test, t_test
# 下載mnist資料集
# 分別下載測試影象包、測試標籤包、訓練影象包、訓練標籤包
x, t = get_data()
conv = SimpleConvNet()
# 獲取預訓練好的權重與偏置引數
conv.load_params("E:\\workcode\\code\\DeepLearn_Base\\ch07\\cnn_params.pkl")
# 初始化
batch_size = 100
accuracy_cnt = 0
for i in range(int(x.shape[0] / batch_size)):
# 批次取資料
x_batch = x[i * batch_size : (i+1) * batch_size]
tt = t[i * batch_size : (i+1) * batch_size]
# 執行推理
y_batch = conv.predict(x_batch)
p = np.argmax(y_batch, axis=1)
# 統計預測正確的資料
accuracy_cnt += np.sum(p == tt)
print(f'第 {i} 批次,輸入資料量{(i+1) * batch_size}個,準確預測數為 {accuracy_cnt}')
print("Accuracy:" + str(float(accuracy_cnt) / x.shape[0]))
最後的輸出如下: