一維DFT

1 DFT的相關內容

一維DFT的意義：一維訊號由若干個不同頻率的正餘弦訊號組合而成；
一維DFT的解決問題：確定輸入訊號中有多少個週期訊號，以及週期訊號的幅值、頻率、相位值；
一維DFT的原理：
- 通過取樣頻率fs對原始訊號進行離散化，依次計算離散訊號與各個基訊號的相關性（N為取樣點數對應存在N個基訊號，每個基訊號與離散訊號會有一個複數結果）
一維DFT的求取步驟：
1. 設定取樣頻率fs，對輸入訊號f(t)進行取樣，得到N個取樣點，對應的離散化訊號記作x[n]，n = [0, 1, ..., N) ;
2. 通過DFT公式計算得到N個匹配對X[k]，k= [0, 1, ..., N)，X[k]代表N個取樣點的原始訊號中存在著k個週期的的訊號分量，即第k+1個基訊號；
\[X[k]=Σ_{n=0}^{N-1} x(n){e^{-jA}}=Σ_{n=0}^{N-1} x(n)(cos(A)-jsin(A)), 其中A=2πkn/N. \]
1. 根據總的取樣時長 = N / fs，故對於X[k]≠0時，對應輸入訊號的頻率 f = (k * fs) / N；在k≠0時，幅值為複數X[k]的模除以（N/2），在k=0時，幅值為複數X[k]的模除以 N；相位即為複數X[k]的幅角；
2. 注：因為要滿足取樣定理 fs ≥ 2f，故只使用頻率域的前一半結果，由 f = k*fs/N 可推導；
- 假設，X[2] 的模為不為0, 這說明N個取樣點中有2個週期，故每個週期的時長T =N / (2 ** fs) *，即輸入訊號的頻率 f = (2 * fs) / N；

2 DFT計算結果驗證

DFT計算公式：

\[X[k]=Σ_{n=0}^{N-1} x(n){e^{-jA}}=Σ_{n=0}^{N-1} x(n)(cos(A)-jsin(A)), 其中A=2πkn/N. \]

通過numpy中np.fft.fft() 函數驗證自己實現的程式碼是正確的，程式碼如下

import cmath
import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

np.set_printoptions(edgeitems=3)
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
N = len(arr)
omega = 2 * np.pi / N
mag_ls = []
for k in range(N):
    mag_ls.append(sum([arr[j] * cmath.exp(complex(0, -j * omega * k)) for j in range(N)]))

print(np.array(mag_ls))
# [45.  +0.j    -4.5+12.364j -4.5 +5.363j -4.5 +2.598j -4.5 +0.793j
# -4.5 -0.793j -4.5 -2.598j -4.5 -5.363j -4.5-12.364j]

X = np.fft.fft(arr)
print(X)

# [45.  +0.j    -4.5+12.364j -4.5 +5.363j -4.5 +2.598j -4.5 +0.793j
# -4.5 -0.793j -4.5 -2.598j -4.5 -5.363j -4.5-12.364j]

3 DFT的時頻曲線分析

問題：給定一個連續的輸入訊號 f(t) = 2 + 3 * np.cos(2 * np.pi * 0.2 * t) + 1.5 * np.cos(2 * np.pi * 0.1 * t) ，通過 DFT 來求解輸入訊號中各個周期函數的幅值、頻率、相位值；

思路：參考一維DFT的求取步驟

程式碼實現：

import matplotlib.pyplot as plt
import numpy as np

fs = 0.5    # 取樣頻率 HZ
t = np.arange(0, 100, 1 / fs)   # 時間序列，每隔 1/fs 秒採集一次資料，共採集N次
N = len(t)     # 序列的長度
x = 2 + 3 * np.cos(2 * np.pi * 0.2 * t) + 1.5 * np.cos(2 * np.pi * 0.1 * t)
X = np.fft.fft(x)
m = np.abs(X)
Mag = m.copy()
ifft_x = np.fft.ifft(X)
ifft_m = np.abs(ifft_x)

freq = [k * fs / N for k in range(N)]
m[0] /= N
m[1:] /= (N / 2)
print("freq:", freq)

plt.figure()
name = "f(t) = 2 + 3 * cos(2π * 0.2 * t) + 1.5 * np.cos(2π * 0.1 * t)"
plt.subplot(131), plt.plot(t, x, c="b", marker="o")
plt.title(name), plt.xlabel("取樣週期 t={} 秒".format(1/fs)), plt.ylabel("輸出f(t)")

plt.subplot(132), plt.plot(range(N), Mag, c="g", marker="o"), plt.title("DFT 結果")
plt.title("DFT 結果"), plt.xlabel("基訊號N=[0~{})".format(N)), plt.ylabel("基訊號對應的幅值")

plt.subplot(133), plt.plot(freq, m, c="r", marker="o"), plt.title("DFT 結果")
plt.title("DFT 結果"), plt.xlabel("訊號的頻率".format(N)), plt.ylabel("真實幅值")

plt.figure()
plt.subplot(121), plt.plot(t, x, c="b"), plt.title("原始訊號")
plt.subplot(122), plt.plot(t, ifft_m, c="g"), plt.title("逆DFT訊號")
plt.show()

輸出結果：

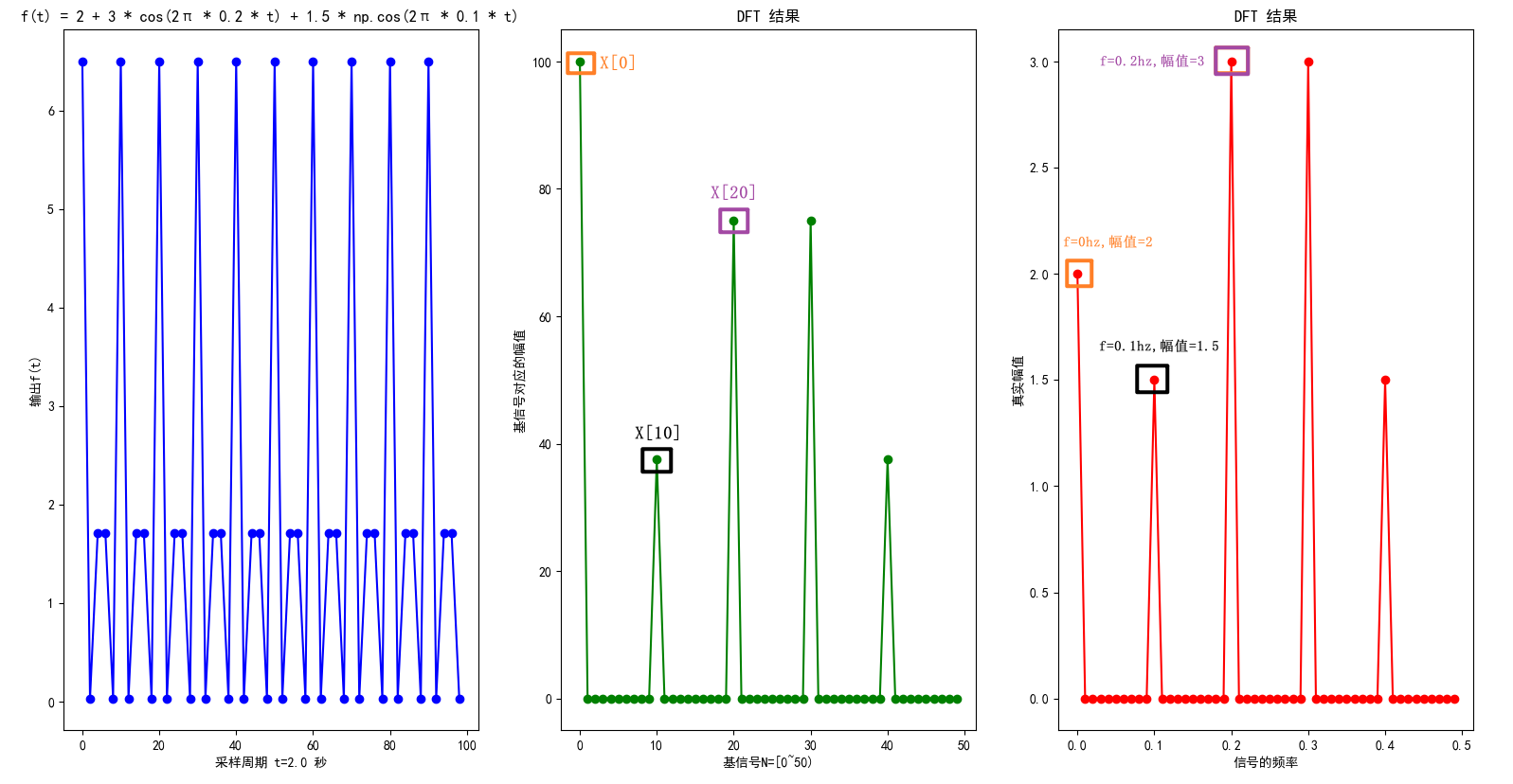
由圖1可知：

fs=0.5hz，取樣點 N = 50， f = k * fs / N，直流分量的幅值 = X[0] 模 / (50)，其它分量的幅值 = X[k] 模 / (25) k≠0
X[0] 對應輸入訊號中2，
X[10] 對應輸入訊號中 1.5 * np.cos(2 * np.pi * 0.1 * t) ，
X[20] 對應輸入訊號中 3 * np.cos(2 * np.pi * 0.2 * t)

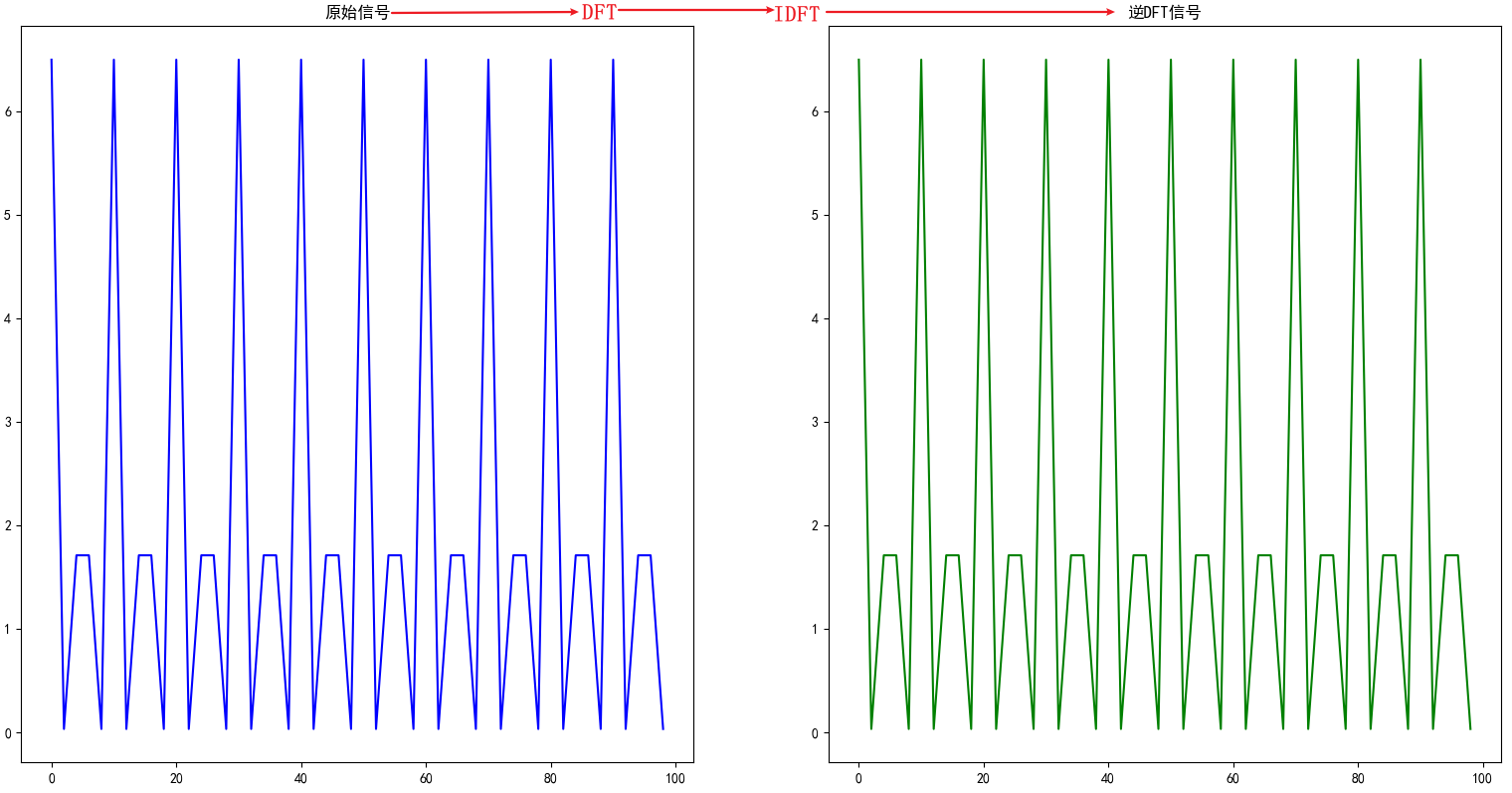
由圖2可知，DFT與IDFT是可逆的

4 DFT的應用

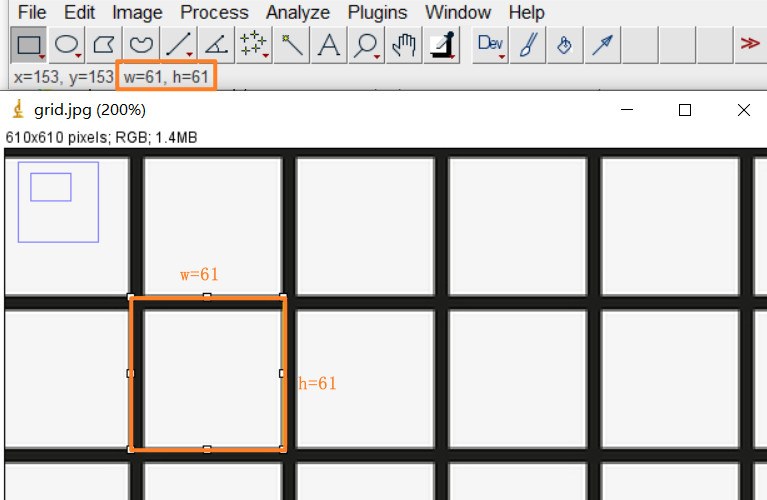
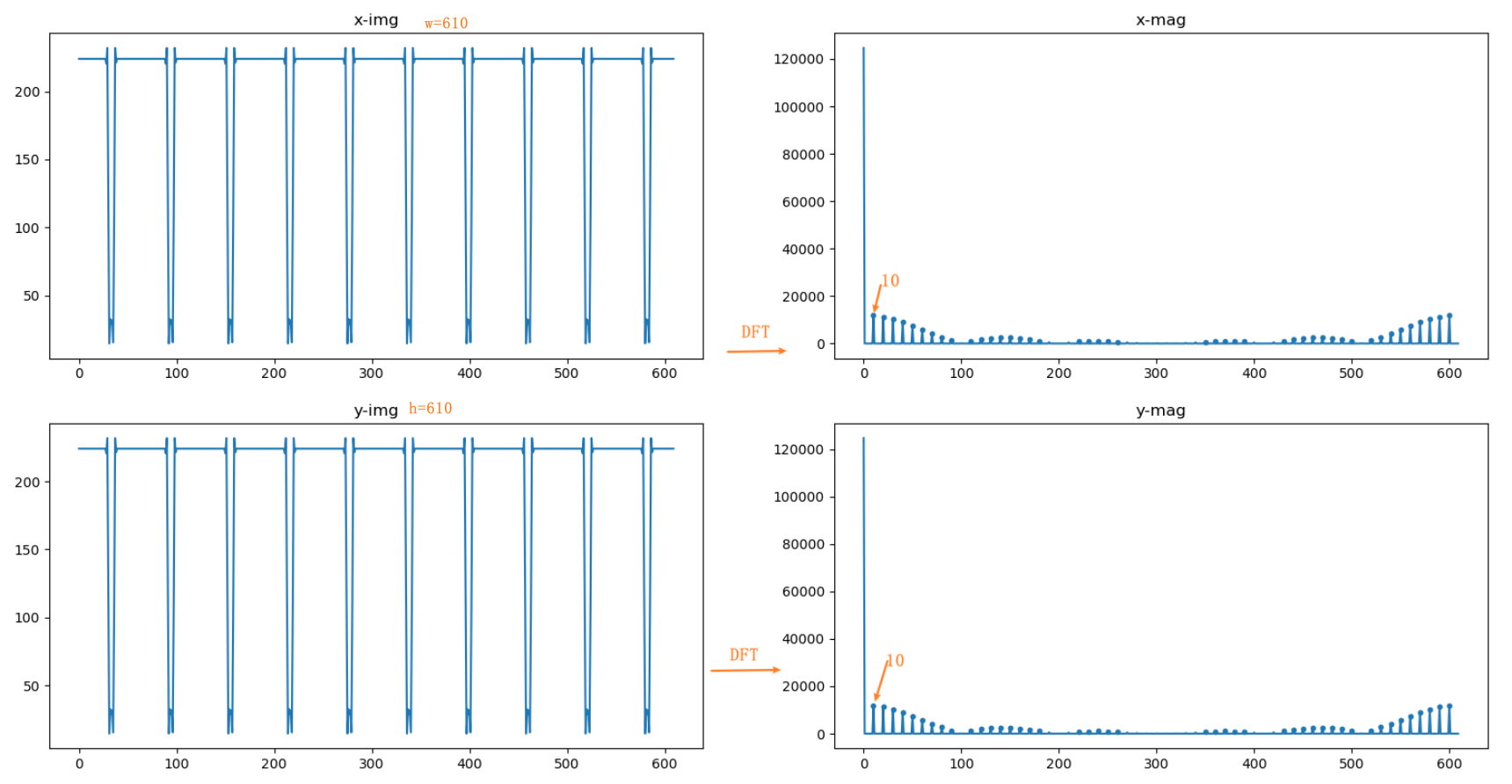
方法：使用DFT求取影象中單個網格的畫素大小， psx = 用影象的寬度除以 x方向上網格的數量，psx = 用影象的高度除以 y方向上網格的數量；

思路：求解psx — 在x方向上求取影象的畫素均值，然後經過DFT變換，得到頻域上的週期訊號，其中週期個數即為網格數量；為了縮小誤差，可以按照一定大小來縮小影象，重複psx 求取過程，通過平均值來提高計算精度；同理 psy一樣。

執行結果：

二維DFT

1 DFT在影象處理時的相關內容

影象中高頻與低頻區別：
- 高頻：變化劇烈的灰度分量，例如邊界
- 低頻：變化緩慢的灰度分量，例如一片大海
傅立葉變換的作用：濾波、影象配準；
- 低通濾波器：只保留低頻，會使得影象模糊
- 高通濾波器：只保留高頻，會使得影象細節增強

2 DFT濾波應用

import cv2
import numpy as np
from matplotlib import pyplot as plt


def DFT(image, isshow=True):
    img_float32 = np.float32(image)

    dft = cv2.dft(img_float32, flags=cv2.DFT_COMPLEX_OUTPUT)
    dft_shift = np.fft.fftshift(dft)
    # 得到灰度圖能表示的形式
    magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

    if isshow:
        plt.subplot(121), plt.imshow(image, cmap='gray')
        plt.title('Input Image'), plt.xticks([]), plt.yticks([])
        plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray')
        plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
        plt.show()

    return dft_shift


def IDFT(image, dft_shift, Filtter="None", isshow=True):
    if Filtter:
        rows, cols = img.shape
        crow, ccol = int(rows / 2), int(cols / 2)  # 中心位置
        mask = None
        if Filtter == "HIGH":
            # 高通濾波
            mask = np.ones((rows, cols, 2), np.uint8)
            mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 0
        elif Filtter == "LOW":
            # 低通濾波
            mask = np.zeros((rows, cols, 2), np.uint8)
            mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 1
        dft_shift = dft_shift * mask

    f_ishift = np.fft.ifftshift(dft_shift)
    img_back = cv2.idft(f_ishift)
    img_back = cv2.magnitude(img_back[:, :, 0], img_back[:, :, 1])

    if isshow:
        plt.subplot(121), plt.imshow(image, cmap='gray')
        plt.title('Input Image'), plt.xticks([]), plt.yticks([])
        plt.subplot(122), plt.imshow(img_back, cmap='gray')
        plt.title('Result'), plt.xticks([]), plt.yticks([])
        plt.show()


    return img_back

if __name__ == "__main__":
    img = cv2.imread('lena.jpg', 0)
    fshift = DFT(img)
    IDFT(img, fshift, Filtter="LOW")