機器學習
本文深入探討了似然函數的基礎概念、與概率密度函數的關係、在最大似然估計以及機器學習中的應用。通過詳盡的定義、舉例和Python/PyTorch程式碼範例,文章旨在提供一個全面而深入的理解。
關注TechLead,分享AI全維度知識。作者擁有10+年網際網路服務架構、AI產品研發經驗、團隊管理經驗,同濟本復旦碩,復旦機器人智慧實驗室成員,阿里雲認證的資深架構師,專案管理專業人士,上億營收AI產品研發負責人。

一、概要
在機器學習和統計學領域中,似然函數(Likelihood Function)是一個至關重要的概念。它不僅是引數估計的基礎,而且在模型選擇、模型評估以及眾多先進的演演算法和技術中都有著廣泛的應用。本文旨在全面但深入地探討似然函數,從其基本定義和性質到在不同機器學習問題中的具體應用。
文章將首先介紹似然函數與概率密度函數的關係,然後通過最大似然估計(Maximum Likelihood Estimation, MLE)來展示如何利用似然函數進行引數估計。接著,我們會探討似然函數在分類問題和迴歸問題中的應用,並使用Python和PyTorch程式碼段進行範例演示。
為了保持文章的技術深度,我們還將討論模型選擇與似然比檢驗,以及似然函數在最新研究進展中的角色,如在貝葉斯方法和複雜模型優化中的應用。
二、什麼是似然函數
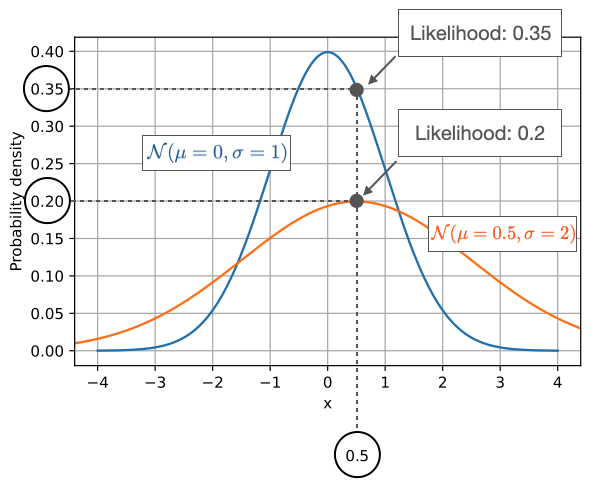
似然函數是一個在統計學和機器學習中經常出現的概念,它用於描述給定引數下,觀察到某一資料樣本的"可能性"。似然函數通常被記作 ( L(\theta \mid x) ),其中 ( \theta ) 是模型引數,( x ) 是觀察到的資料。
數學定義
數學上,似然函數可以定義為:

似然與概率的區別
- 概率: 描述在固定的引數 ( \theta ) 下,某一事件 ( x ) 發生的可能性。
- 似然: 描述已經觀察到事件 ( x ),而引數 ( \theta ) 是什麼的可能性。
簡單來說,概率是用來描述資料的生成模型,而似然是用來描述引數的合理性。
重要性
似然函數是許多統計推斷方法的基礎,包括但不限於:
- 最大似然估計(MLE)
- 貝葉斯推斷
- 似然比檢驗
舉例
考慮一個投擲硬幣的例子,其中硬幣正面出現的概率是 ( p ),反面出現的概率是 ( 1-p )。
若我們觀察到了3次正面和2次反面,似然函數可以寫作:

通過這一節,我們理解了似然函數的基礎定義,區別和重要性,並通過一個簡單的例子加深了理解。在接下來的部分,我們將更深入地探討似然函數在機器學習和統計學中的應用。
三、似然函數與概率密度函數
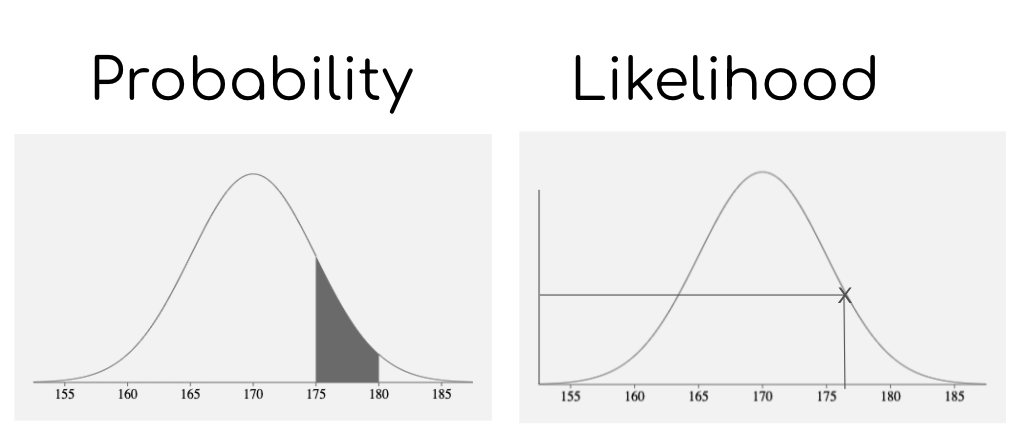
似然函數(Likelihood Function)和概率密度函數(Probability Density Function,簡稱PDF)都是描述資料和引數關係的重要數學工具。儘管兩者在形式上具有相似性,它們在解釋、用途和計算方面有著明顯的不同。本節將詳細介紹這兩個概念的定義、區別和應用場景,並通過具體例子進行解釋。
似然函數(Likelihood Function)
定義
似然函數用於量化在給定某引數值時,觀察到某一資料樣本的「可能性」。數學上,似然函數的定義如下:

例子
考慮一個簡單的擲硬幣實驗,假設硬幣正面出現的概率是 ( p )。若投擲了5次,出現了3次正面,2次反面。在這種情況下,似然函數可以表示為:

概率密度函數(Probability Density Function, PDF)
定義
概率密度函數描述了一個連續隨機變數在各個特定值上的「密度」,也就是該值出現的相對可能性。對於離散隨機變數,這個概念被稱為概率質量函數(Probability Mass Function, PMF)。

區別與聯絡
- 角色互換: 在概率密度函數中,引數是固定的,我們考慮資料的變化。在似然函數中,資料是已知的,我們考慮引數的變化。
- 目的不同: 概率密度函數用於描述資料生成模型,而似然函數用於基於觀察到的資料進行引數估計。
- 數學性質: 概率密度函數需要滿足概率的公理(如非負性,積分(或求和)為1),而似然函數沒有這樣的要求。
四、最大似然估計(Maximum Likelihood Estimation, MLE)
最大似然估計是一種常用的引數估計方法,它通過最大化似然函數來找到最「合適」的引數值。在這一節中,我們將詳細講解最大似然估計的基礎理論、應用場景,並通過具體的例子與程式碼演示進行解釋。
定義與基本思想

例子與程式碼:估計正態分佈的引數

Python程式碼實現
下面是使用Python和PyTorch來實現最大似然估計的程式碼。
import torch
import torch.optim as optim
# 隨機生成一些正態分佈的資料樣本(均值為5,標準差為2)
data = torch.normal(5, 2, size=(100,))
# 初始化引數
mu = torch.tensor(1.0, requires_grad=True)
sigma = torch.tensor(1.0, requires_grad=True)
# 優化器
optimizer = optim.SGD([mu, sigma], lr=0.01)
# 迭代次數
n_iter = 5000
# 開始優化
for i in range(n_iter):
optimizer.zero_grad()
# 計算負對數似然
n = len(data)
neg_log_likelihood = 0.5 * n * torch.log(2 * torch.tensor(3.14159)) + n * torch.log(sigma) + torch.sum((data - mu)**2) / (2 * sigma**2)
# 反向傳播
neg_log_likelihood.backward()
# 更新引數
optimizer.step()
# 輸出結果
print(f"Estimated mu: {mu.data}")
print(f"Estimated sigma: {sigma.data}")
輸入與輸出
- 輸入:一個來自正態分佈的資料樣本(
data)。 - 輸出:估計得到的均值(
mu)和標準差(sigma)。
處理過程
- 初始化均值和標準差的引數。
- 使用梯度下降法來最小化負對數似然函數。
通過以上的定義、例子和程式碼,最大似然估計在引數估計中的重要性和實用性得以充分展示。在接下來的部分,我們將繼續深入探討如何使用似然函數進行更復雜的模型選擇和評估。
五、似然函數在機器學習中的應用
似然函數不僅在統計推斷中有重要應用,也在機器學習,尤其是在監督學習、非監督學習以及模型選擇等方面有廣泛的使用。本節將深入探討似然函數在機器學習各領域中的應用,並提供相關的程式碼範例。
監督學習:邏輯迴歸
定義
在監督學習中,特別是用於分類問題的邏輯迴歸模型,最大似然估計用於優化模型的引數。邏輯迴歸模型試圖找到一個函數,使得給定輸入特徵下某一類別出現的「可能性」最大。
例子與程式碼:邏輯迴歸模型

以下是用PyTorch實現邏輯迴歸模型的程式碼:
import torch
import torch.nn as nn
import torch.optim as optim
# 建立一些簡單的資料
x_data = torch.tensor([[1.0], [2.0], [3.0], [4.0]])
y_data = torch.tensor([[0], [0], [1], [1]], dtype=torch.float32)
# 定義模型
class LogisticRegressionModel(nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = nn.Linear(1, 1)
def forward(self, x):
y_pred = torch.sigmoid(self.linear(x))
return y_pred
model = LogisticRegressionModel()
# 損失和優化器
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 訓練模型
for epoch in range(1000):
model.train()
optimizer.zero_grad()
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
loss.backward()
optimizer.step()
# 輸出訓練後的引數
print("Weight:", model.linear.weight.item())
print("Bias:", model.linear.bias.item())
輸入與輸出
- 輸入:特徵 (x) 和標籤 (y)。
- 輸出:邏輯迴歸模型的引數。
處理過程
- 初始化模型和優化器。
- 使用二元交叉熵損失函數(對應於邏輯迴歸的負對數似然函數)。
- 通過梯度下降來更新模型的引數。
六、總結
在本篇部落格中,我們從似然函數的基礎概念出發,深入探討了它在統計推斷和機器學習中的多方面應用。無論是在引數估計的最大似然估計法,還是在邏輯迴歸和高斯混合模型中,似然函數都發揮著至關重要的作用。通過最大化似然函數,我們不僅能找到描述資料的「最合適」的模型引數,而且還可以更深入地理解模型的性質和限制。
-
似然函數與梯度下降:在機器學習中,尤其是深度學習領域,梯度下降是最常用的優化演演算法。然而,不同的損失函數(即負對數似然函數)可能導致不同的優化效能和模型泛化能力。理解似然函數如何與梯度下降演演算法互動,有助於我們更有效地訓練模型。
-
模型選擇與複雜度:在現實應用中,選擇一個「最佳」模型通常涉及到複雜度與準確性之間的權衡。通過似然函數,我們可以更直觀地評估模型複雜度與資料擬合度之間的關係,從而進行更合理的模型選擇。
-
似然函數與不確定性:在現實世界的很多問題中,資料往往具有噪聲和不確定性。似然函數為我們提供了一種量化不確定性的方式,進一步,我們甚至可以通過貝葉斯方法,將先驗資訊與似然函數相結合,以更全面地理解資料和模型。
-
似然函數與生成模型:在非監督學習和生成模型(如GANs)中,似然函數的概念有時會被重新定義或拓展,以適應更復雜或高維的資料結構。理解這些擴充套件或變種的數學基礎,可以為研究和應用這些先進模型提供有力的支撐。
通過深入探討似然函數和最大似然估計,本文旨在為讀者提供一個全面而深入的理解,幫助大家更有效地應用這一概念於各種實際問題中。無論你是統計學家,還是機器學習研究者,甚至是工程師,理解和掌握似然函數都將是你走向專業化、高效解決問題之路上的重要一步。
關注TechLead,分享AI全維度知識。作者擁有10+年網際網路服務架構、AI產品研發經驗、團隊管理經驗,同濟本復旦碩,復旦機器人智慧實驗室成員,阿里雲認證的資深架構師,專案管理專業人士,上億營收AI產品研發負責人。
如有幫助,請多關注
TeahLead KrisChang,10+年的網際網路和人工智慧從業經驗,10年+技術和業務團隊管理經驗,同濟軟體工程本科,復旦工程管理碩士,阿里雲認證雲服務資深架構師,上億營收AI產品業務負責人。