圖文剖析 big.js 四則運算原始碼
big.js,一個小型、快速的用於任意精度的十進位制算術的JavaScript 庫。
big.js 用於解決平常專案中進行算術運算時精度丟失引起的結果不準確的問題。和 big.js 類似的兩個庫 bignumber.js 和 decimal.js 也都是出自同一作者(MikeMcl)之手。
作者在 這裡 詳細說明了他們之間的區別
big.js是最小的任意精度的計算庫。big.js是三者中最小也最簡單的,它只有bignumber.js一半的方法,不到bignumber.js的一半大。
bignumber.js和decimal.js儲存值的進位制比big.js更高,因此當操作大量數位時,前兩者的速度會更快。
bignumber.js可能更適合金融類應用,因為使用者不用擔心丟失精度,除非使用了涉及除法的操作。
這篇文章分別就 big.js 的解析函數,以及加減乘除運算的原始碼進行剖析,瞭解作者的設計思路。在四則運算的原始碼中,相比加減乘,除法運算最為複雜。
用法
建立 Big 物件時,new 操作符是可選的
x = new Big(123.4567)
y = Big('123456.7e-3') // 'new' is optional
z = new Big(x)
x.eq(y) && x.eq(z) && y.eq(z) // true
建構函式
建構函式中關鍵程式碼如下
function Big(n) {
var x = this;
// 使用建構函式前面可以不帶 new 關鍵字
if (!(x instanceof Big)) return n === UNDEFINED ? _Big_() : new Big(n);
// 如果傳進來的引數已經是 Big 的範例物件,則複製一份,否則使用 parse 函數建立一個範例物件
if (n instanceof Big) {
x.s = n.s;
x.e = n.e;
x.c = n.c.slice();
} else {
if (typeof n !== 'string') {
if (Big.strict === true && typeof n !== 'bigint') {
throw TypeError(INVALID + 'value');
}
// 傳入的如果是 -0 ,則轉為字串表示 '-0'
n = n === 0 && 1 / n < 0 ? '-0' : String(n);
}
parse(x, n);
}
使用建構函式前面可以不帶 new 關鍵字
如果傳進來的引數已經是 Big 的範例物件,則將範例物件的屬性複製一份,否則使用 parse 函數為範例物件建立屬性。
parse 函數
function parse(x, n) {
var e, i, nl;
// NUMERIC = /^-?(\d+(\.\d*)?|\.\d+)(e[+-]?\d+)?$/i;
if (!NUMERIC.test(n)) {
throw Error(INVALID + 'number');
}
// Determine sign.
x.s = n.charAt(0) == '-' ? (n = n.slice(1), -1) : 1;
// Decimal point?
if ((e = n.indexOf('.')) > -1) n = n.replace('.', '');
// Exponential form?
if ((i = n.search(/e/i)) > 0) {
// Determine exponent.
if (e < 0) e = i;
e += +n.slice(i + 1);
n = n.substring(0, i);
} else if (e < 0) {
// Integer.
e = n.length;
}
nl = n.length;
// Determine leading zeros.
for (i = 0; i < nl && n.charAt(i) == '0';) ++i;
if (i == nl) {
// Zero.
x.c = [x.e = 0];
} else {
// Determine trailing zeros.
for (; nl > 0 && n.charAt(--nl) == '0';);
x.e = e - i - 1;
x.c = [];
// Convert string to array of digits without leading/trailing zeros.
for (e = 0; i <= nl;) x.c[e++] = +n.charAt(i++);
}
return x;
}
parse 函數會為範例物件新增三個屬性;
x.s,表示數位的符號,即是正數還是負數,即正負值,若是正數,x.s = 1,負數則為 -1x.e,表示數位對應的指數表示法的指數,比如n = 1234的指數為3x.c,數位陣列,比如1234轉換後是 [1,2,3,4]
1234 會被轉化為
{
c:[1,2,3,4],
e:3,
s:1
}
這種表示,和 IEEE 754 雙精度浮點數的儲存方式 很類似,而 JavaScript 的 Number型別就是一個雙精度 64 位二進位制格式 IEEE 754 值使用 64 位來表示 3 個部分:
- 1 位用於表示符號(sign) (正數或者負數)
- 11 位用於表示指數(exponent) (-1022 到 1023)
- 52 位用於表示尾數(mantissa) (表示 0 和 1 之間的數值)

下面分析 parse 函數轉化的詳細過程,以 Big('123400'),Big('0.1234'),Big('100e2') 為例
注意:Big('100e2') 中 100e2 以字串形式傳進來才能檢測到 e ,Number形式的 Big(100e2),執行 parse 前會被轉化為 Big(10000)
- 校驗傳入的值,只允許數位,
'.1',指數形式的寫法。比如2.34,.2,10e2
// NUMERIC = /^-?(\d+(\.\d*)?|\.\d+)(e[+-]?\d+)?$/i;
if (!NUMERIC.test(n)) {
throw Error(INVALID + 'number');
}
Big('123400'),Big('-0.1234'),Big('100e2') 都通過
x.s = n.charAt(0) == '-' ? (n = n.slice(1), -1) : 1;確定符號
Big('123400') => x.s = 1
Big('-0.1234') => x.s = -1 並且 -0.1234 => 0.1234
Big('100e2') => x.s = 1
if ((e = n.indexOf('.')) > -1) n = n.replace('.', '');是否含有小數點,如果是,則刪除小數點,並將 e 的初始值設為小數點的位置
Big('123400') => x.e = -1 , n = 123400
Big('-0.1234') => x.e = 1 , n = 01234
Big('100e2') => x.e = -1 , n = 100e2
- 如果數位是科學表示法,比如
100e2,e 的位置是 3,e 後面的指數是 2 ,則 x.e = 3 + 2
if ((i = n.search(/e/i)) > 0) {
// Determine exponent.
if (e < 0) e = i;
e += +n.slice(i + 1);
n = n.substring(0, i);
} else if (e < 0) {
// Integer.
e = n.length;
}
Big('123400')
x.e = -1 => x.e = n.length = 6
n = 123400
Big('-0.1234')
x.e = 1
n = 01234
Big('100e2')
x.e = -1 => x.e = e 在 100e2 中的位置 + e 後面緊跟的指數係數 = 3 + 2 = 5
n = 100e2 => n = 100
nl = n.length;nl 表示傳進來的數位的長度
Big('123400')
x.e = 6
n = 123400
nl = 6
Big('-0.1234')
x.e = 1
n = 01234
nl = 5
Big('100e2')
x.e = 5
n = 100
nl = 3
for (i = 0; i < nl && n.charAt(i) == '0';) ++i;確定數位是否有前置 0 ,這裡的 i 表示第一個不為 0 的數位的位置,也可以表示數位前面有多少個 0
Big('123400')
x.e = 6
n = 123400
nl = 6
i = 0
Big('-0.1234')
x.e = 1
n = 01234
nl = 5
i = 1
Big('100e2')
x.e = 5
n = 100
nl = 3
i = 0
- 如果 i = nl,則說明傳進來的輸入是一個 0 或者多個 0
if (i == nl) {
// Zero.
x.c = [x.e = 0];
} else {
// 排除尾隨 0,nl 為最後一個不為 0 的數位的位置
for (; nl > 0 && n.charAt(--nl) == '0';);
x.e = e - i - 1;
x.c = [];
// 傳進來的數位,排除掉前置 0 和尾隨 0 後,轉換為數位陣列
for (e = 0; i <= nl;) x.c[e++] = +n.charAt(i++);
}
Big('123400')
//因為預設 e 是 n.length,而Big指數表示是 1.234 * 10^5,所以這裡 x.e 要減一
x.e = 6 => x.e = e - i - 1 = 6 - 0 - 1 = 5
n = 123400
nl = 6 => 排除尾隨 0,nl 為最後一個不為 0 的數位的位置 => nl = 3
i = 0
x.c => 選取 n 中從 i 到 nl 的數位組成陣列 [1,2,3,4]
Big('-0.1234')
x.e = 1 => x.e = e - i - 1 = 1 - 1 - 1 = -1
n = 01234
nl = 5 => 排除尾隨 0,nl 為最後一個不為 0 的數位的位置 => nl = 4
i = 1
x.c => 選取 n 中從 i 到 nl 的數位組成陣列 [1,2,3,4]
Big('100e2')
x.e = 5 => x.e = e - i - 1 = 5 - 0 - 1 = 4
n = 100
nl = 3 => 排除尾隨 0,nl 為最後一個不為 0 的數位的位置 => nl = 0
i = 0
x.c => 選取 n 中從 i 到 nl 的數位組成陣列 [1]
最後 Big('123400'),Big('-0.1234'),Big('100e2') 將轉換為
Big('123400')
x.s = 1
x.e = 5
x.c = [1,2,3,4]
Big('-0.1234')
x.s = -1
x.e = -1
x.c = [1,2,3,4]
Big('100e2')
x.s = 1
x.e = 4
x.c = [1]
至此 parse 函數邏輯結束,接下來分別剖析下加減乘除運算;
加法
原始碼
P.plus = P.add = function (y) {
var e, k, t,
x = this,
Big = x.constructor;
y = new Big(y);
// 校驗符號是否不同
if (x.s != y.s) {
y.s = -y.s;
return x.minus(y);
}
var xe = x.e,
xc = x.c,
ye = y.e,
yc = y.c;
// 校驗是否是 0
if (!xc[0] || !yc[0]) {
if (!yc[0]) {
if (xc[0]) {
y = new Big(x);
} else {
y.s = x.s;
}
}
return y;
}
xc = xc.slice();
// 前面加上零使指數均衡
// Note: reverse faster than unshifts.
if (e = xe - ye) {
if (e > 0) {
ye = xe;
t = yc;
} else {
e = -e;
t = xc;
}
t.reverse();
for (; e--;) t.push(0);
t.reverse();
}
// 讓 xc 存放長度更長的數位
if (xc.length - yc.length < 0) {
t = yc;
yc = xc;
xc = t;
}
e = yc.length;
for (k = 0; e; xc[e] %= 10) k = (xc[--e] = xc[e] + yc[e] + k) / 10 | 0;
// No need to check for zero, as +x + +y != 0 && -x + -y != 0
if (k) {
xc.unshift(k);
++ye;
}
// 刪除尾隨 0
for (e = xc.length; xc[--e] === 0;) xc.pop();
y.c = xc;
y.e = ye;
return y;
};
- 如果符號不同,則轉為減法運算;比如 -x + y 就是 y - x ,x + -y 就是 x - y
if (x.s != y.s) {
y.s = -y.s;
return x.minus(y);
}
- 其中兩個數位是不是 0,其中有一個為 0,則直接返回另外一個
if (!xc[0] || !yc[0]) {
if (!yc[0]) {
if (xc[0]) {
y = new Big(x);
} else {
y.s = x.s;
}
}
return y;
}
- 比較指數冪差,較小的一方,在前面補零,方便後續加法操作;並且將指數冪較大的一方,作為兩數相加的結果的指數冪的初始值。
if (e = xe - ye) {
if (e > 0) {
ye = xe; // 將指數冪較大的一方,作為兩數相加的結果的指數冪的初始值
t = yc;
} else {
e = -e;
t = xc;
}
t.reverse();
for (; e--;) t.push(0);
t.reverse();
}
比如 1234 + 12
1234 在範例物件上是以數位陣列形式表示 [1,2,3,4]
12 則是 [1,2]
為方便後續陣列按照位置進行加法運算,這裡需要給 12 補零
[1,2,3,4]
+
[0,0,1,2]
- xc 存放長度更長的數位
if (xc.length - yc.length < 0) {
t = yc;
yc = xc;
xc = t;
}
- 接下來是加法邏輯
e = yc.length;
for (k = 0; e; xc[e] %= 10) k = (xc[--e] = xc[e] + yc[e] + k) / 10 | 0;
if (k) {
xc.unshift(k);
++ye;
}
// 刪除尾隨 0
for (e = xc.length; xc[--e] === 0;) xc.pop();
k 儲存進位的值
- 初始化進位值為 0 ,e 為 yc 長度,執行下面迴圈體
(xc[--e] = xc[e] + yc[e] + k)計算 xc[e] 加上 yc[e] 加上上一次計算結果進位的值;- 隨後 xc[--e] 儲存計算後的進位的數值,e--
- 最後 xc[e] 儲存計算後的個位數值
上面過程用圖例表示如下
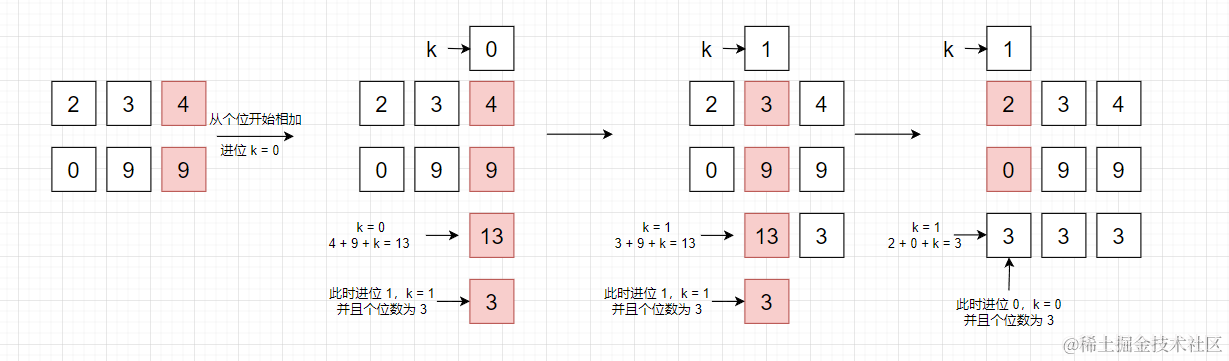
減法
原始碼
P.minus = P.sub = function (y) {
var i, j, t, xlty,
x = this,
Big = x.constructor,
a = x.s,
b = (y = new Big(y)).s;
// 確定符號,x - (-y) = x + y - x - y = -x + (-y)
if (a != b) {
y.s = -b;
return x.plus(y);
}
var xc = x.c.slice(),
xe = x.e,
yc = y.c,
ye = y.e;
// 判斷是否為 0
if (!xc[0] || !yc[0]) {
if (yc[0]) {
y.s = -b;
} else if (xc[0]) {
y = new Big(x);
} else {
y.s = 1;
}
return y;
}
// 比較兩數指數冪大小,給指數冪小的一方補零,方便後續相減;
// 比如 1234 - 23 parse函數解析後 => [1,2,3,4] - [2,3] 為了使 [2,3] 對應十位,個位
// 在前面補 0 ,即 [1,2,3,4] - [0,0,2,3]
// 再比如 66 - 233 parse函數解析後 => [6,7] - [2,3,3],同樣為了使 6,7對應十位,個位
// 在前面補 0 ,即 [0,6,7] - [2,3,3]
if (a = xe - ye) {
if (xlty = a < 0) {
a = -a;
t = xc;
} else {
ye = xe;
t = yc;
}
t.reverse();
for (b = a; b--;) t.push(0); // 補零
t.reverse();
} else {
// 若指數冪相等,不需要補零,則比較兩數大小,從最大位開始比較;
// 比如 [2,3,4] 和 [1,2,3] 最大位是百位,若百位的數位不相等,則可得出孰大孰小
j = ((xlty = xc.length < yc.length) ? xc : yc).length;
for (a = b = 0; b < j; b++) {
if (xc[b] != yc[b]) {
xlty = xc[b] < yc[b];
break;
}
}
}
// 對於被減數 x 和減數 y
// 如果 x - y < 0,則交換兩數,並改變符號;比如 2 - 4 = -(4-2)
if (xlty) {
t = xc;
xc = yc;
yc = t;
y.s = -y.s;
}
// 如果被減數的數位陣列長度小於減數,則給被減數的末尾新增 0
// 比如 12 - 0.0009 parse函數解析後 => [1,2] - [0,0,0,0,9]
// 因為 9 是小數後幾位,相應的需要給 [1,2]末尾補 0 ,即 [1,2,0,0,0] - [0,0,0,0,9]
if ((b = (j = yc.length) - (i = xc.length)) > 0) for (; b--;) xc[i++] = 0;
// 從 xc 中減去 yc
for (b = i; j > a;) {
if (xc[--j] < yc[j]) {
for (i = j; i && !xc[--i];) xc[i] = 9;
--xc[i];
xc[j] += 10;
}
xc[j] -= yc[j];
}
// 去掉運算結果末尾 0
for (; xc[--b] === 0;) xc.pop();
// 去掉運算結果前置 0 ,並減去相應指數冪
for (; xc[0] === 0;) {
xc.shift();
--ye;
}
// 運算結果為 0 的情況
if (!xc[0]) {
// n - n = +0
y.s = 1;
xc = [ye = 0];
}
y.c = xc;
y.e = ye;
return y;
};
減法前面的邏輯和加法類似,這裡不再贅述,已在上面程式碼註釋中說明,下面是減法的核心邏輯
// 從 被減數 xc 中減去減數 yc
// a 是 xc 和 yc 的冪的差值,j 是 yc 的長度,這裡迴圈條件用 j > a,表示迴圈 j-a 次
// 比如 120 - 9 => [1,2,0]-[0,0,9] 指數冪差是 2 ,減數數位陣列長度是 3 ,則只需要迴圈 3-2=1 次
// 比如 120 - 0.009 => [1,2,0,0,0,0]-[0,0,0,0,0,9] 指數冪差是 5 ,減數數位陣列長度是 6 ,則只需要迴圈 6-5=1 次
for (b = i; j > a;) {
if (xc[--j] < yc[j]) {
//從後往前遍歷xc,當碰到值為0 ,將值改為 9;
//比如 [1,0,0]-[0,0,9] => [0,9,10] -
for (i = j; i && !xc[--i];) xc[i] = 9;
--xc[i];
xc[j] += 10;
}
xc[j] -= yc[j];
}
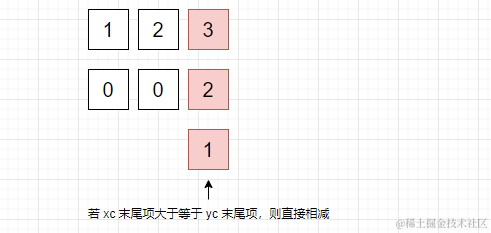
上面過程用圖例表示如下,xc 表示被減數,yc 表示減數
1、若 xc 末尾項大於等於 yc 末尾項,比如 [1,2,3]和[0,0,2],則直接相減。
2、若 xc 末尾項小於 yc 末尾項,則執行以下邏輯
for (i = j; i && !xc[--i];) xc[i] = 9;
上面程式碼錶示從 當前進行相減運算的元素的位置(j) 往前遍歷被減數 xc 每個元素,當元素值為 0 時,將值改為 9,直至上一個元素值不為 0 ,迴圈結束。
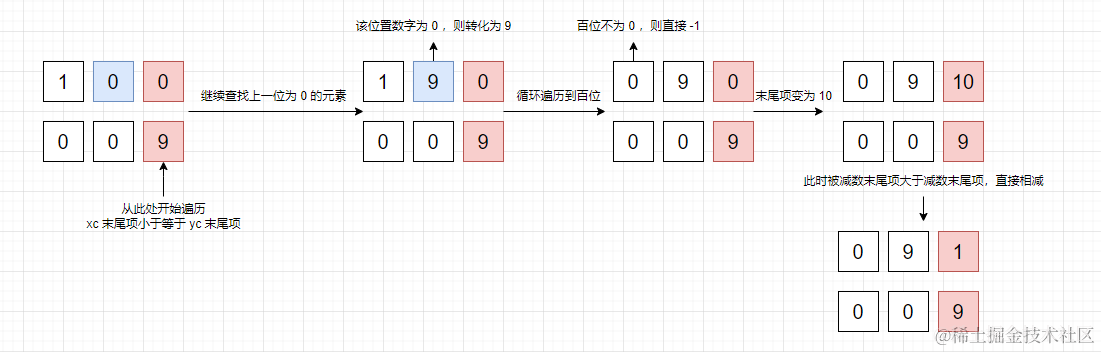
至此,減法邏輯結束。
乘法
原始碼
P.times = P.mul = function (y) {
var c,
x = this,
Big = x.constructor,
xc = x.c,
yc = (y = new Big(y)).c,
a = xc.length,
b = yc.length,
i = x.e,
j = y.e;
// 確定結果的符號
y.s = x.s == y.s ? 1 : -1;
// 其中一個為 0 ,返回結果為 0
if (!xc[0] || !yc[0]) {
y.c = [y.e = 0];
return y;
}
// 初始化結果的指數
y.e = i + j;
// 對比 xc,yc 長度,xc 存放長度更長的一方
if (a < b) {
c = xc;
xc = yc;
yc = c;
j = a;
a = b;
b = j;
}
// 用 0 初始化結果陣列
for (c = new Array(j = a + b); j--;) c[j] = 0;
// i is initially xc.length.
for (i = b; i--;) {
b = 0;
// a is yc.length.
for (j = a + i; j > i;) {
// Current sum of products at this digit position, plus carry.
b = c[j] + yc[i] * xc[j - i - 1] + b;
c[j--] = b % 10;
// carry
b = b / 10 | 0;
}
c[j] = b;
}
// 如果有最終進位,則增加結果的指數,否則刪除頭部的 0
if (b) ++y.e;
else c.shift();
// 刪除尾部的 0
for (i = c.length; !c[--i];) c.pop();
y.c = c;
return y;
};
乘法原始碼的主要邏輯是下面這一段
for (i = b; i--;) {
b = 0;
for (j = a + i; j > i;) {
// 當前數位位置的總和,加上進位
b = c[j] + yc[i] * xc[j - i - 1] + b;
c[j--] = b % 10;
// 進位值
b = b / 10 | 0;
}
c[j] = b;
}
描述的其實就是以前老師教我們在紙上乘法運算的過程:
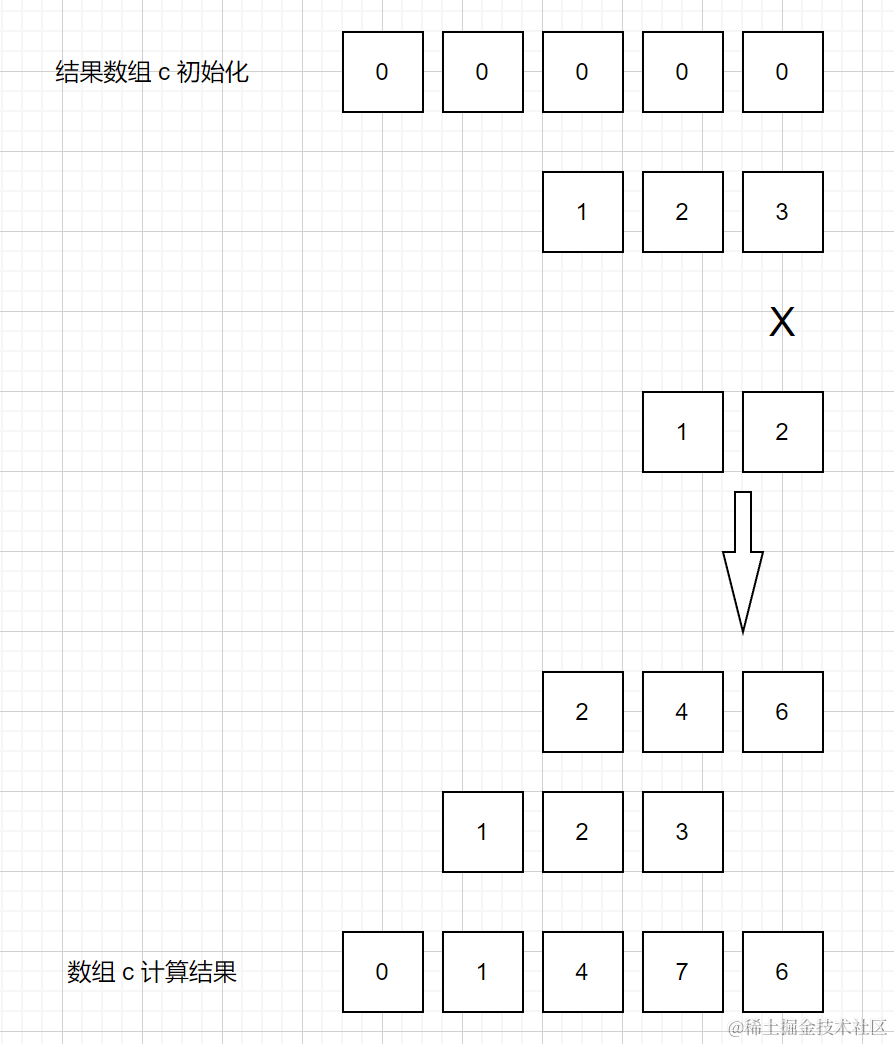
以 123*12 來舉例子分析上面這段程式碼
-
xc 是乘數 [1,2,3],yc 是被乘數 [1,2],b 是 yc 長度,a 是 xc 長度
-
c 是儲存結果的陣列,定義的長度是 a+b
兩個數相乘得到的結果長度可能是 a+b,也有可能是 a+b-1。所以後面需要刪除陣列頭部的 0
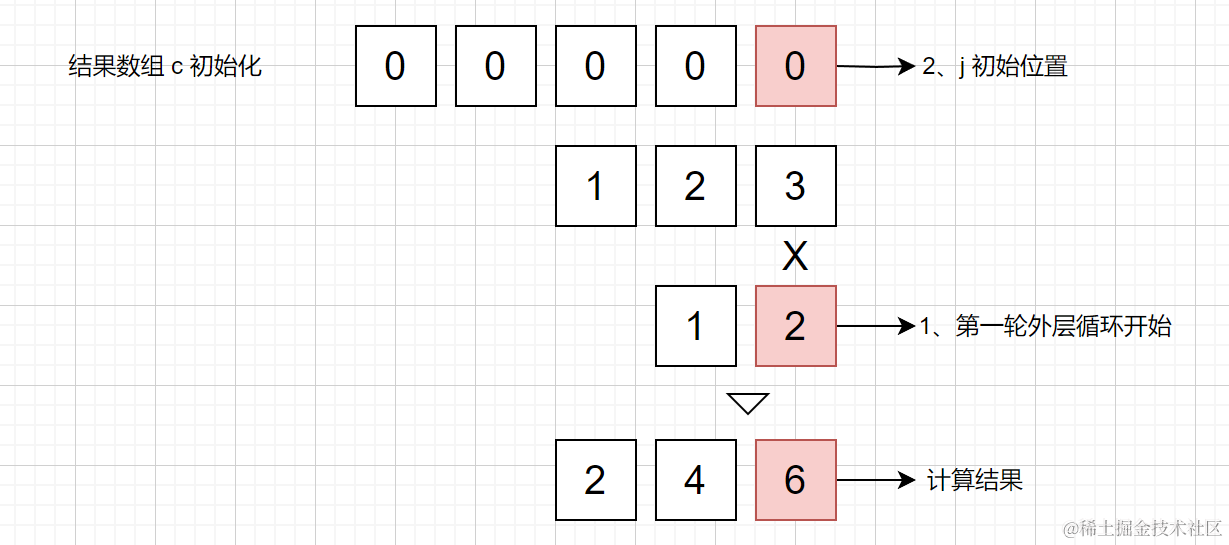
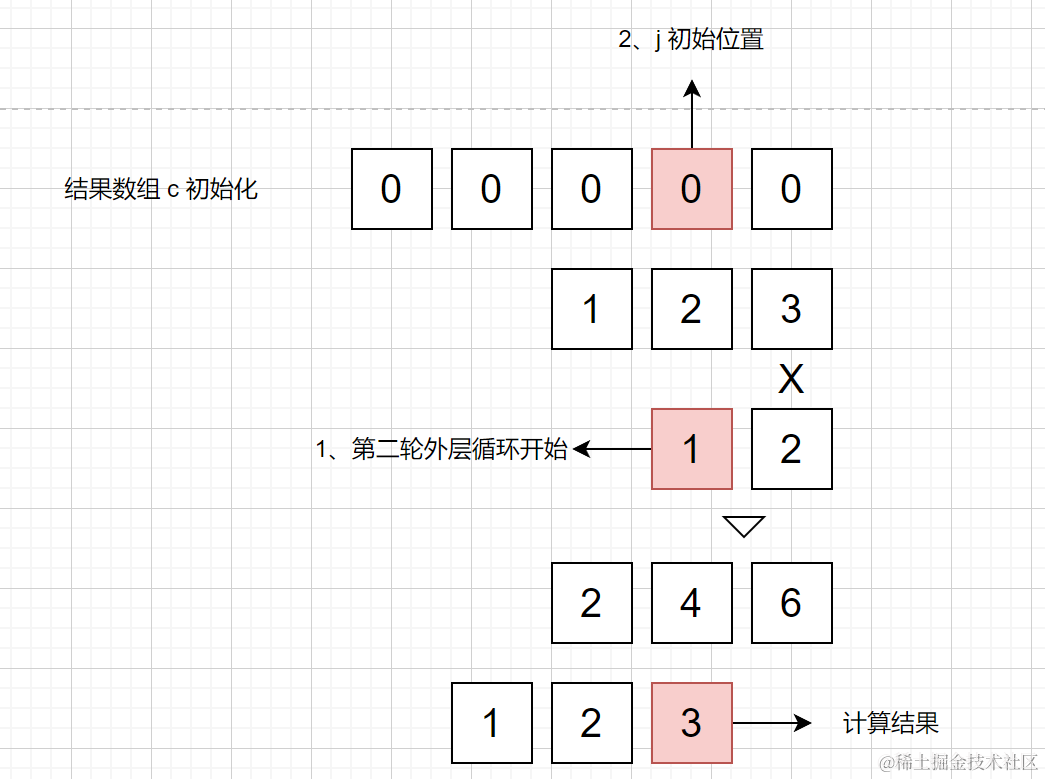
for (i = b; i--;)首先是外層迴圈,從陣列長度較短的被乘數開始迴圈,將 b 賦值給 i,i 充當 yc 的長度,而 b 用來儲存進位的值b = 0定義進位的值for (j = a + i; j > i;)內層乘數(123)的迴圈,這裡的 j 表示在結果陣列 c 中的位置
for (j = a + i; j > i;)實際上就是 for ( j = 乘數長度 + 當前被乘數數位的位置 ),這裡是因為當第二輪外層迴圈時,123 * 1 的時候,1 是 12 的 十位,所以在 j 也應該從十位開始儲存計算結果。
第一輪外層迴圈
第二輪外層迴圈
b = c[j] + yc[i] * xc[j - i - 1] + b當前數位位置的總和,加上進位
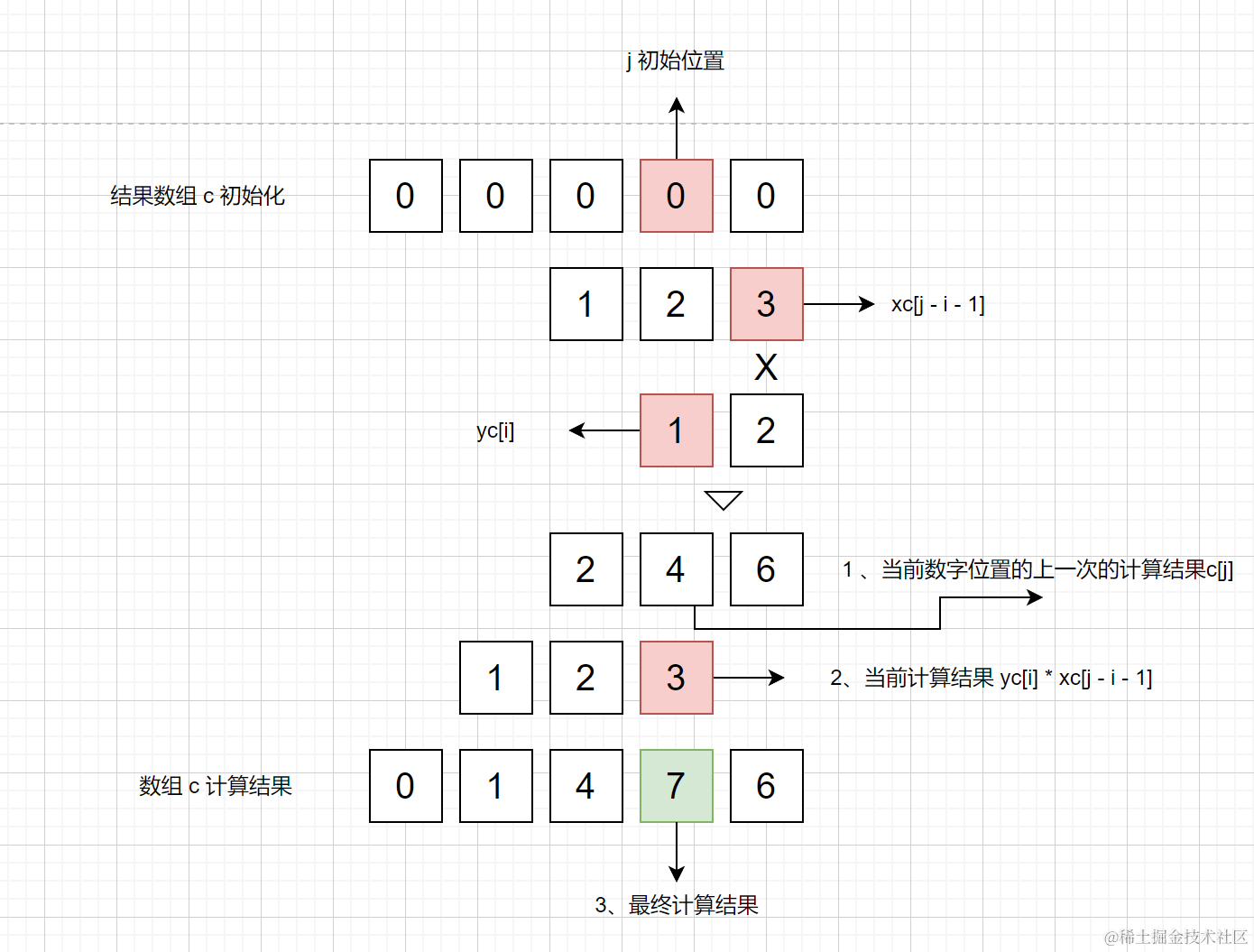
c[j--] = b % 10;當前位置去整取餘b = b / 10 | 0;進位值取整
至此乘法運算邏輯結束
除法
原始碼
P.div = function (y) {
var x = this,
Big = x.constructor,
a = x.c, // dividend
b = (y = new Big(y)).c, // divisor
k = x.s == y.s ? 1 : -1,
dp = Big.DP;
if (dp !== ~~dp || dp < 0 || dp > MAX_DP) {
throw Error(INVALID_DP);
}
// Divisor is zero?
if (!b[0]) {
throw Error(DIV_BY_ZERO);
}
// Dividend is 0? Return +-0.
if (!a[0]) {
y.s = k;
y.c = [y.e = 0];
return y;
}
var bl, bt, n, cmp, ri,
bz = b.slice(),
ai = bl = b.length,
al = a.length,
r = a.slice(0, bl), // remainder
rl = r.length,
q = y, // quotient
qc = q.c = [],
qi = 0,
p = dp + (q.e = x.e - y.e) + 1; // precision of the result
q.s = k;
k = p < 0 ? 0 : p;
// Create version of divisor with leading zero.
bz.unshift(0);
// Add zeros to make remainder as long as divisor.
for (; rl++ < bl;) r.push(0);
do {
// n is how many times the divisor goes into current remainder.
for (n = 0; n < 10; n++) {
// Compare divisor and remainder.
if (bl != (rl = r.length)) {
cmp = bl > rl ? 1 : -1;
} else {
for (ri = -1, cmp = 0; ++ri < bl;) {
if (b[ri] != r[ri]) {
cmp = b[ri] > r[ri] ? 1 : -1;
break;
}
}
}
// If divisor < remainder, subtract divisor from remainder.
if (cmp < 0) {
// Remainder can't be more than 1 digit longer than divisor.
// Equalise lengths using divisor with extra leading zero?
for (bt = rl == bl ? b : bz; rl;) {
if (r[--rl] < bt[rl]) {
ri = rl;
for (; ri && !r[--ri];) r[ri] = 9;
--r[ri];
r[rl] += 10;
}
r[rl] -= bt[rl];
}
for (; !r[0];) r.shift();
} else {
break;
}
}
// Add the digit n to the result array.
qc[qi++] = cmp ? n : ++n;
// Update the remainder.
if (r[0] && cmp) r[rl] = a[ai] || 0;
else r = [a[ai]];
} while ((ai++ < al || r[0] !== UNDEFINED) && k--);
// Leading zero? Do not remove if result is simply zero (qi == 1).
if (!qc[0] && qi != 1) {
// There can't be more than one zero.
qc.shift();
q.e--;
p--;
}
// Round?
if (qi > p) round(q, p, Big.RM, r[0] !== UNDEFINED);
return q;
};
在除法運算中,對於 a/b , a 是被除數,b 是除數,下面依次分析上面程式碼
if (dp !== ~~dp || dp < 0 || dp > MAX_DP)判斷 dp 是不是大於 0 的整數,並且小於 MAX_DP,這裡的 dp 可以自己設定
Big.DP = 30
- 除數為 0 則丟擲錯誤。
if (!b[0]) {
throw Error(DIV_BY_ZERO);
}
- 被除數是 0 則返回值為 0 的範例物件
if (!a[0]) {
y.s = k;
y.c = [y.e = 0];
return y;
}
- 接下來是除法運算邏輯,定義變數的那一段不貼了,直接看 do while 迴圈
do {
// n 是迴圈次數,表示從當前位置的餘數中可以分出多少個除數來,也就是當前位置的商。
for (n = 0; n < 10; n++) {
// 比較除數和餘數大小
if (bl != (rl = r.length)) {
cmp = bl > rl ? 1 : -1;
} else {
for (ri = -1, cmp = 0; ++ri < bl;) {
if (b[ri] != r[ri]) {
cmp = b[ri] > r[ri] ? 1 : -1;
break;
}
}
}
// 除數小於餘數,則繼續從餘數中減去除數
if (cmp < 0) {
// Remainder can't be more than 1 digit longer than divisor.
// Equalise lengths using divisor with extra leading zero?
for (bt = rl == bl ? b : bz; rl;) {
if (r[--rl] < bt[rl]) {
ri = rl;
for (; ri && !r[--ri];) r[ri] = 9;
--r[ri];
r[rl] += 10;
}
r[rl] -= bt[rl];
}
for (; !r[0];) r.shift();
} else {
break;
}
}
// qc 陣列儲存商
qc[qi++] = cmp ? n : ++n;
// 更新餘數
if (r[0] && cmp) r[rl] = a[ai] || 0;
else r = [a[ai]];
} while ((ai++ < al || r[0] !== UNDEFINED) && k--);
這個迴圈做了這些事情:以 1234 / 9 為例;
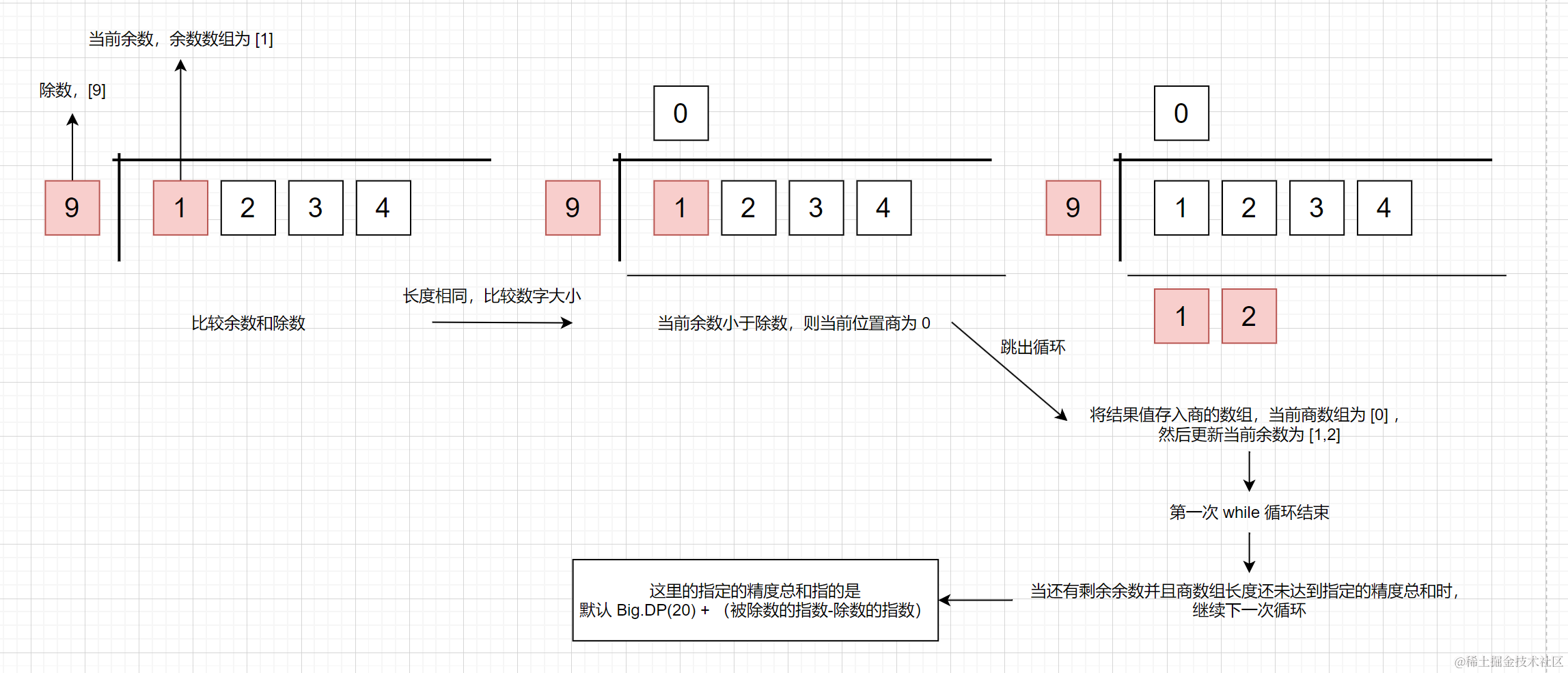
- 將當前位置的餘數 1 和除數 9 比較大小,(一開始餘數取的是被除數的前面 n 位,n 和除數的長度大小相同,所以取的是 1 )。先比較長度,長度相同再比較大小。
- 若除數大於當前位置餘數,則跳出迴圈(當前迴圈次數即為當前位置的商,9 > 1 ,那麼當前迴圈次數為 0 ,即當前位置商為 0 )
- 然後儲存商
qc[qi++] = cmp ? n : ++n; - 最後更新當前餘數,除數大於餘數時,則當前餘數向後借一位,餘數就由 1 變為了 12
if (r[0] && cmp) r[rl] = a[ai] || 0;
else r = [a[ai]];
- 若除數小於當前餘數,則繼續從餘數中減去除數 (開始減法 for 迴圈)
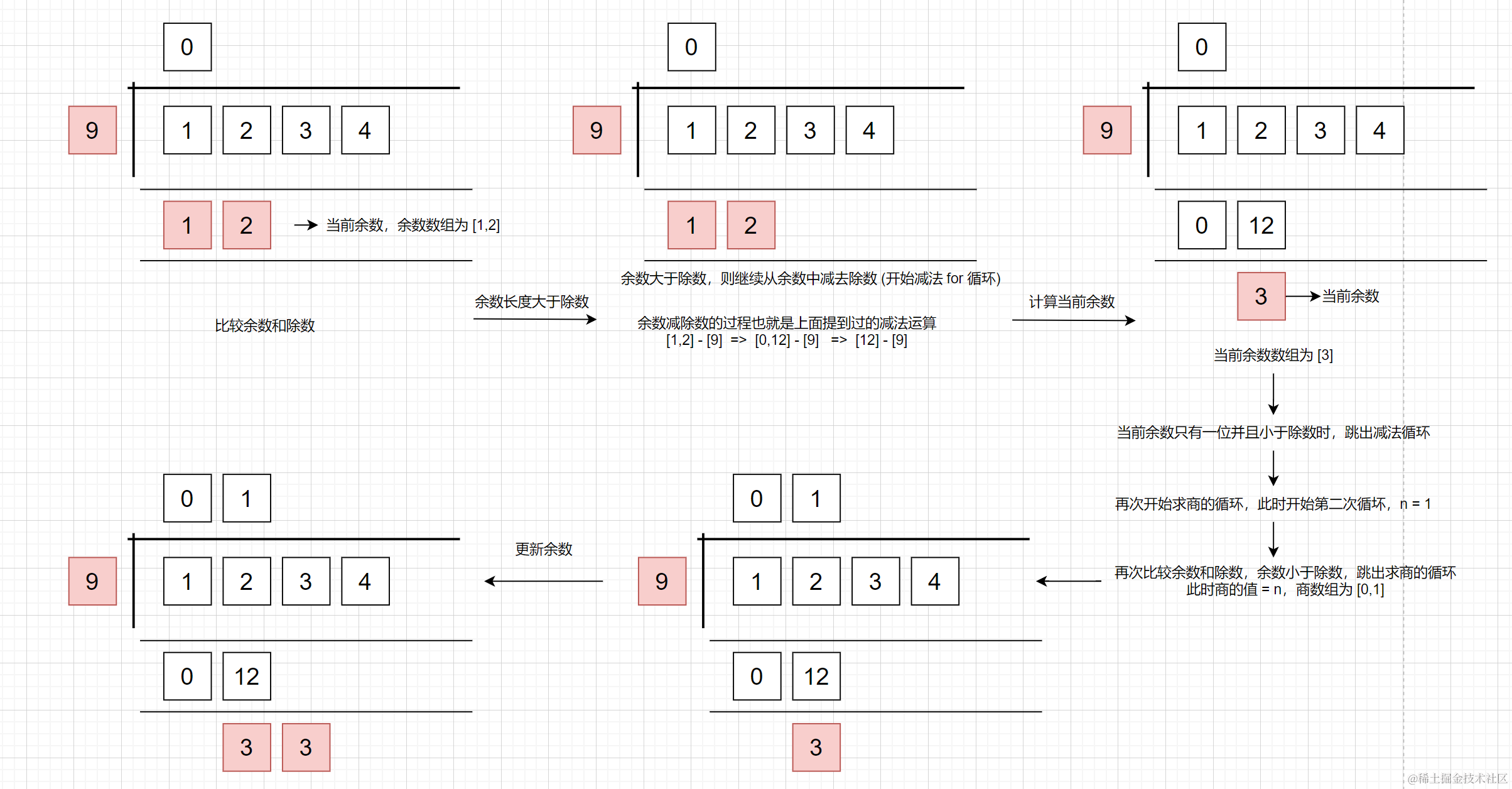
- 然後再次儲存商
qc[qi++] = cmp ? n : ++n; - 然後再次更新當前餘數,除數大於餘數時,則當前餘數向後借一位,餘數就由 3 變為了 33
- 當商陣列的長度沒有達到指定的精度總和,繼續上面的步驟,直至迴圈結束;
指定的精度總和指的是 Big.DP(預設20) + (被除數的指數-除數的指數); 1234 / 9 的指定精度總和是 23。
- 商陣列長度大於 1 的情況下,刪除陣列前面的 0 ;如果是 商就是 0 ,比如 0/1 = 0,這種情況不必刪除 0 了
if (!qc[0] && qi != 1) {
qc.shift();
q.e--;
p--;
}
- 舍入操作
if (qi > p) round(q, p, Big.RM, r[0] !== UNDEFINED);
至此除法邏輯結束
注意事項
big.js 用陣列儲存值,類似 高精度計算,只不過 big.js 是陣列中每個位置儲存一個值,然後對每個位置進行運算;而對超級大的數位(數百或數千位數值時),big.js 算術運算不如 bignumber.js 快。
例如,bignumber.js 將數位1234.56789的數位儲存為[1234,56789000000000] ,即以兩個1e14為基數的陣列形式儲存,而 big.js 儲存的數位與[1,2,3,4.5,6,7,8,9]相同,即以9個10為基數的陣列形式儲存。前者的算術運算可能更快,因為需要處理的元素較少。在實踐中,這可能只有在使用數百或數千位數值時才會有所不同。
在使用 big.js 進行運算時需要注意有時候沒有設定足夠大的精度,會導致結果不是想要的。
Big.DP = 20
+Big(1).div('11111111').times('11111111') // 0.9999999999999999
// 0.9999999999999999 在 Number 編碼的可以表示的準確精度範圍內
Big.DP = 30
+Big(1).div('11111111').times('11111111') // 1
// 而設定 Big.DP = 30 後
//結果陣列儲存的是 999999999999999999999999
//超過了 Number 編碼的可以表示的準確精度範圍,則會舍入為 1
總結
本文剖析了 big.js 解析函數原始碼,四則運算原始碼,分別用圖文詳細描述了運算過程,一步步還原了作者的構思。有不正確的地方或者不同見解還請各位大佬提出來。