期望最大化（EM）演演算法：從理論到實戰全解析

本文深入探討了期望最大化（EM）演演算法的原理、數學基礎和應用。通過詳盡的定義和具體例子，文章闡釋了EM演演算法在高斯混合模型（GMM）中的應用，並通過Python和PyTorch程式碼實現進行了實戰演示。

關注TechLead，分享AI全維度知識。作者擁有10+年網際網路服務架構、AI產品研發經驗、團隊管理經驗，同濟本復旦碩，復旦機器人智慧實驗室成員，阿里雲認證的資深架構師，專案管理專業人士，上億營收AI產品研發負責人。

一、引言

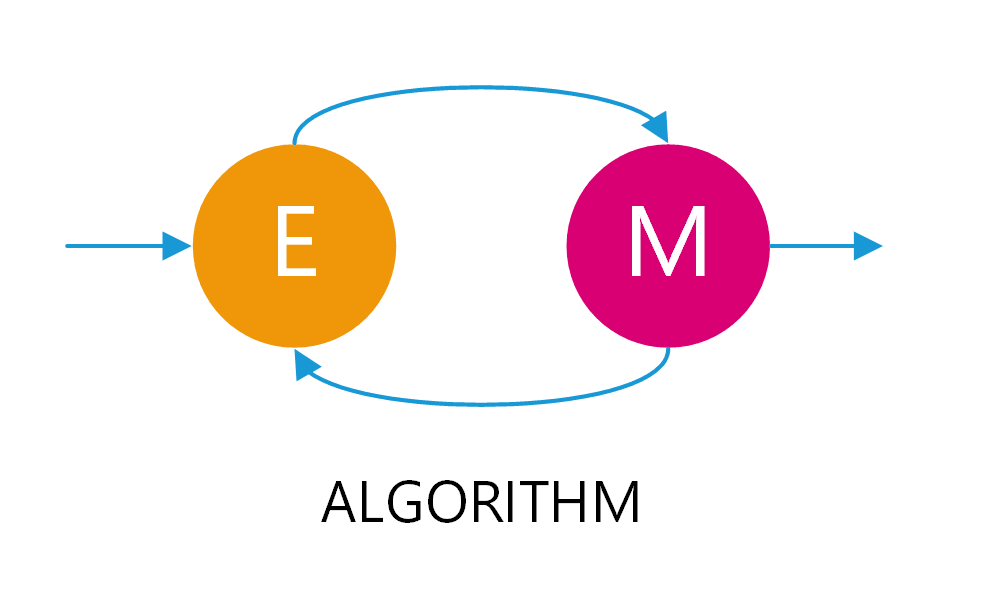
期望最大化演演算法（Expectation-Maximization Algorithm，簡稱EM演演算法）是一種迭代優化演演算法，主要用於估計含有隱變數（latent variables）的概率模型引數。它在機器學習和統計學中有著廣泛的應用，包括但不限於高斯混合模型（Gaussian Mixture Model, GMM）、隱馬爾可夫模型（Hidden Markov Model, HMM）以及各種聚類和分類問題。

概率模型與隱變數

概率模型是一種用數學表示的資料生成過程。在統計學和機器學習中，一個概率模型通常用來描述觀測資料（observable data）和潛在結構（latent structure）之間的關係。

例子：假設我們有一個資料集，包含了一群人的身高和體重。一個簡單的概率模型可能假設身高和體重都符合正態分佈。

隱變數（Latent Variables）是指那些不能直接觀測到，但會影響到觀測資料的變數。在包含隱變數的概率模型中，通常更難以進行引數估計。

例子：在推斷一群人是否喜歡運動的情況下，我們可能能觀測到他們的身高和體重，但「是否喜歡運動」這一隱變數是無法直接觀測的。

極大似然估計（MLE）

極大似然估計（Maximum Likelihood Estimation, MLE）是一種用於估計概率模型引數的方法。它通過尋找一組引數，使得給定觀測資料出現的可能性（即似然函數）最大化。

例子：在一個硬幣投擲實驗中，觀測到了10次正面和15次反面，MLE會尋找一個引數（硬幣正面朝上的概率），使得觀測到這樣的資料最有可能。

Jensen不等式

Jensen不等式是凸優化理論中的一個基本不等式，常用於證明EM演演算法的收斂性。簡單地說，Jensen不等式表明對於一個凸函數，函數在凸組合上的值不會大於凸組合中各點值的平均。

二、基礎數學原理

在理解EM演演算法的工作機制之前，我們需要掌握一些關鍵的數學概念和原理。這些原理不僅形成了EM演演算法的數學基礎，而且也有助於我們理解演演算法的收斂性和效率。

條件概率與聯合概率

似然函數

Kullback-Leibler散度

貝葉斯推斷

貝葉斯推斷是一種基於貝葉斯定理的引數估計和模型選擇方法。它使用先驗概率、似然函數和證據（或歸一化因子）來計算引數的後驗概率。

例子：在垃圾郵件分類中，貝葉斯推斷可以用於更新垃圾郵件（或非垃圾郵件）的概率，每當使用者標記一個新郵件時。

這些數學原理為我們提供了理解EM演演算法所需的堅實基礎。通過了解這些概念，我們可以更深入地探討EM演演算法如何進行引數估計，特別是在存在隱變數的複雜模型中。

三、EM演演算法的核心思想

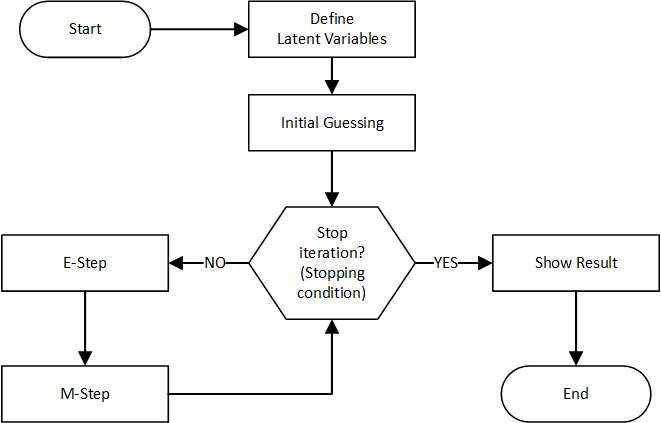
EM演演算法的主要目的是找到含有隱變數的概率模型的引數估計。這一目標在直接應用極大似然估計（MLE）困難或不可行時尤為重要。EM演演算法通過交替執行兩個步驟來實現這一目標：期望（E）步驟和最大化（M）步驟。

期望（E）步驟

期望步驟（Expectation step）涉及計算隱變數給定觀測資料和當前引數估計的條件期望。這通常用於構建一個函數，稱為Q函數，來近似目標函數（通常是似然函數）。

例子：在高斯混合模型中，期望步驟涉及計算每個觀測資料點屬於各個高斯分佈的條件概率，這些概率也稱為後驗概率。

最大化（M）步驟

最大化步驟（Maximization step）則是在給定Q函數的情況下，尋找能使Q函數最大化的引數值。

例子：繼續上面的高斯混合模型例子，最大化步驟涉及調整每個高斯分佈的均值和方差，以最大化由期望步驟得到的Q函數。

Q函數與輔助函數

Q函數是EM演演算法中的一個核心概念，用於近似目標函數（如似然函數）。Q函數通常依賴於觀測資料、隱變數和模型引數。

例子：在高斯混合模型的EM演演算法中，Q函數基於觀測資料和各個高斯分佈的後驗概率來定義。

輔助函數（Auxiliary Function）是EM演演算法的一個重要組成部分，用於保證演演算法收斂。通過最大化輔助函數，我們間接地最大化了似然函數。

例子：在一些文字分類問題中，輔助函數可以通過拉格朗日乘數法來構建，以簡化最大化問題。

收斂性

在EM演演算法中，由於使用了Jensen不等式和輔助函數，演演算法保證會收斂到區域性最大值。

例子：在實施高斯混合模型的EM演演算法後，你會發現每次迭代都會導致似然函數的值增加（或保持不變），直到達到區域性最大值。

通過深入探討這些核心概念和步驟，我們能更全面地理解EM演演算法是如何工作的，以及為什麼它在處理含有隱變數的複雜概率模型時如此有效。

四、EM演演算法與高斯混合模型（GMM）

高斯混合模型（Gaussian Mixture Model，GMM）是一種使用高斯概率密度函數（pdf）為基礎構建的概率模型。它是EM演演算法應用的一個典型例子，尤其是當我們要對資料進行聚類或者密度估計時。

高斯混合模型的定義

高斯混合模型是由多個高斯分佈組成的。每一個高斯分佈稱為一個分量（component），並且每一個分量都有其自己的均值（(\mu)）和方差（(\sigma^2)）。

例子：假設一個資料集呈現出兩個明顯不同的簇。一個高斯混合模型可能會用兩個高斯分佈來描述這兩個簇，每個分佈有自己的均值和方差。

分量權重

每個高斯分量在模型中都有一個權重（(\pi_k)），這個權重描述了該分量對整個資料集的「重要性」。

例子：在一個由兩個高斯分佈組成的GMM中，如果一個分佈的權重為0.7，另一個為0.3，這意味著第一個分佈對整個模型的影響較大。

E步驟在GMM中的應用

在GMM中的E步驟，我們計算資料點對每個高斯分量的後驗概率，即給定資料點，它來自某個特定分量的概率。

例子：假設一個資料點(x)，在E步驟中，我們計算它來自GMM中每個高斯分量的後驗概率。

# 使用Python和PyTorch計算後驗概率
import torch
from torch.distributions import MultivariateNormal

# 假設有兩個分量
means = [torch.tensor([0.0]), torch.tensor([5.0])]
variances = [torch.tensor([1.0]), torch.tensor([2.0])]
weights = [0.6, 0.4]

# 資料點
x = torch.tensor([1.0])

# 計算後驗概率
posterior_probabilities = []
for i in range(2):
    normal_distribution = MultivariateNormal(means[i], torch.eye(1) * variances[i])
    posterior_probabilities.append(weights[i] * torch.exp(normal_distribution.log_prob(x)))

# 歸一化
sum_probs = sum(posterior_probabilities)
posterior_probabilities = [prob / sum_probs for prob in posterior_probabilities]

print("後驗概率:", posterior_probabilities)

M步驟在GMM中的應用

在M步驟中，我們根據E步驟計算出的後驗概率來更新每個高斯分量的引數（均值和方差）。

例子：假設從E步驟中獲得了資料點對於兩個高斯分量的後驗概率，我們會用這些後驗概率來加權地更新均值和方差。

通過詳細地探討高斯混合模型和它與EM演演算法的關聯，我們更深入地理解了這一複雜模型是如何工作的，以及EM演演算法在其中扮演了什麼角色。這不僅有助於我們理解演演算法的數學基礎，還為實際應用提供了實用的見解。

五、實戰案例

在實戰案例中，我們將使用Python和PyTorch來實現一個簡單的高斯混合模型（GMM）以展示EM演演算法的應用。

定義：目標

我們的目標是對一維資料進行聚類。我們將使用兩個高斯分量（也就是說，K=2）。

例子：假設我們有一個一維資料集，其中包含兩個簇。我們希望使用GMM模型找到這兩個簇的引數（均值和方差）。

定義：輸入和輸出

輸入：一維資料陣列
輸出：兩個高斯分量的引數（均值和方差）以及它們的權重。

實現步驟

初始化引數：為均值、方差和權重設定初始值。
E步驟：計算資料點屬於每個分量的後驗概率。
M步驟：使用後驗概率更新均值、方差和權重。
收斂檢查：檢查引數是否收斂。如果沒有，則返回第2步。

# Python和PyTorch程式碼實現
import torch
from torch.distributions import Normal

# 初始化引數
means = torch.tensor([0.0, 5.0])
variances = torch.tensor([1.0, 1.0])
weights = torch.tensor([0.5, 0.5])

# 假設的一維資料集
data = torch.cat((torch.randn(100) * 1.5, torch.randn(100) * 0.5 + 5))

# EM演演算法實現
for iteration in range(100):
    # E步驟
    posterior_probabilities = []
    for i in range(2):
        normal_distribution = Normal(means[i], torch.sqrt(variances[i]))
        posterior_probabilities.append(weights[i] * torch.exp(normal_distribution.log_prob(data)))
        
    # 歸一化
    sum_probs = torch.stack(posterior_probabilities).sum(0)
    posterior_probabilities = [prob / sum_probs for prob in posterior_probabilities]

    # M步驟
    for i in range(2):
        responsibility = posterior_probabilities[i]
        means[i] = torch.sum(responsibility * data) / torch.sum(responsibility)
        variances[i] = torch.sum(responsibility * (data - means[i])**2) / torch.sum(responsibility)
        weights[i] = torch.mean(responsibility)

    # 輸出當前引數
    print(f"Iteration {iteration+1}: Means = {means}, Variances = {variances}, Weights = {weights}")

結果解釋

在執行以上程式碼後，你將看到均值、方差和權重的引數在每次迭代後都會更新。當這些引數不再顯著變化時，我們可以認為演演算法已經收斂。

輸入：一維資料集，包含兩個簇。
輸出：每次迭代後的均值、方差和權重。

通過這個實戰案例，我們不僅演示瞭如何在PyTorch中實現EM演演算法，並且通過具體的程式碼範例深入理解了演演算法的每一個步驟。這樣的內容安排旨在滿足你對於概念豐富、充滿細節和定義完整的需求。

六、總結

經過詳盡的理論分析和實戰範例，我們對期望最大化（EM）演演算法有了更全面的瞭解。從基礎數學原理到具體的實現和應用，EM演演算法展示了其在統計模型引數估計中的強大能力，特別是當我們面臨缺失或隱含資料時。

概率模型的選擇：雖然我們在實戰中使用了高斯混合模型（GMM），但EM演演算法並不僅限於此。事實上，它可以應用於任何滿足特定條件的概率模型，這一點在研究和應用更為複雜的資料結構時尤為重要。
初始化的重要性：本文提到了引數的初始選擇，但實際應用中應更加小心。糟糕的初始化可能導致演演算法陷入區域性最優，從而影響模型效能。
收斂性和效率：儘管EM演演算法通常能保證收斂，但收斂速度可能是一個問題，特別是在高維資料和複雜模型中。這一點可能會促使我們尋找更有效的優化演演算法或者採用分散式計算。
模型解釋性與複雜性的權衡：EM演演算法能夠估計複雜模型的引數，但這種複雜性可能會導致模型解釋性降低。在實際應用中，我們需要仔細考慮這種權衡。
演演算法的泛化能力：EM演演算法不僅用於聚類問題，在自然語言處理、計算生物學等多個領域也有廣泛應用。瞭解其核心思想和工作機制能為處理不同型別的資料問題提供有力的工具。

通過深入地探討這些技術洞見，我們不僅加深了對EM演演算法核心概念和工作機制的理解，還能更好地將這一演演算法應用到各種實際問題中。希望這篇文章能進一步促進你對於複雜概率模型和期望最大化演演算法的理解，也希望你能在自己的專案或研究中找到這些資訊的實際應用。

關注TechLead，分享AI全維度知識。作者擁有10+年網際網路服務架構、AI產品研發經驗、團隊管理經驗，同濟本復旦碩，復旦機器人智慧實驗室成員，阿里雲認證的資深架構師，專案管理專業人士，上億營收AI產品研發負責人。
如有幫助，請多關注
TeahLead KrisChang，10+年的網際網路和人工智慧從業經驗，10年+技術和業務團隊管理經驗，同濟軟體工程本科，復旦工程管理碩士，阿里雲認證雲服務資深架構師，上億營收AI產品業務負責人。