具體數學

本文是閱讀《具體數學》產生的理解性文字，並且涵蓋了部分其他相關的內容。

不怎麼重要或者太難的東西因為時間問題，我略過了。

本文來之不易，請勿機械搬運：原文地址 - https://www.cnblogs.com/jeefy/p/17848037.html

第二章 - 和式

和式的處理

和式是一切的基礎，其三個法則十分重要：

其中 \((1.1)\) 代表著分配律，\((1.2)\) 代表的結合律，而 \((1.3)\) 代表的交換律。

我們可以通過這三種法則證明高斯給出的等差數列求和的公式：

其中 \(0 \to 1 \to 2\) 我們用了兩次交換律，在 \(4\) 用了結合律，在 \(5\) 用了分配律。

常常我們化簡式子可能就是這些法則的排列組合。

對於多重和式，我們有著一個新的技巧：交換求和次序

其中 \([P(j, k)]\) 是用於驗證 \(j, k\) 的組合是否合法的符號，如果合法則為 \(1\)，反之為 \(0\)。

也就是說我們並不在意我們到底先列舉的是哪一個變數，但是有些時候列舉另一個變數確實可能簡單很多。

我們可以通過這個法則闡釋矩陣乘法的結合律：

於是我們可以從和式的角度瞭解到矩陣乘法確實滿足結合律。

有限微積分

較好的參考文章：有限微積分與數列求和 - LUNATIC time!

在離散數學中，最小的單位就是 \(1\)，那麼如果要把無限微積分那一套搞過來，那麼 \(Df(x)\) 中的 \(D\) 的含義就必須發生變化。

定義差分運算元 \(\Delta f(x) = f(x + 1) - f(x)\)，可以看到這與 \(Df(x) = \lim_{h \to 0} \frac {f(x + h) - f(x)} h\) 十分的相似。

對於無限微積分來說，\(D(x^n) = n x^{n - 1}\) 是個非常優美的性質。

然而 \(\Delta (x^n)\) 卻是十分的醜陋，於是需要找到新的代替品：

其中 \(x^{\underline n} = x (x - 1) (x - 2) \cdots (x - n + 1)\)。

有了類似的微分，我們需要考慮積分。在無限微積分中，我們有 \(\int_a^b g(x) dx = f(x) \vert_a^b = f(b) - f(a)\)，其中 \(g(x) = Df(x)\)。

而在有限微積分中，我們有另外一個東西：

其中 \(g(x) = \Delta f(x)\)。

這是一個左閉右開區間，所以我們可以簡單的合併幾個和式：\(\sum_a^b + \sum_b^c = \sum_a^c\)。

我們可以通過這個法則簡單的得到 \(x^{\underline n}\) 的求和公式。

考慮 \(\Delta (x^{\underline{n}}) = n x^{\underline{n - 1}}\) 的事實，我們可以推知 \(\frac 1 {m + 1}((x + 1)^{\underline {n + 1}} - (x)^{\underline {n + 1}}) = x^{\underline n}\)。

也就是若 \(g(x) = x^{\underline n}\)，那麼存在 \(f(x) = \frac 1 {n + 1} x^{\underline{n + 1}}\) 滿足 \(\Delta f(x) = g(x)\)。

那麼此時我們可以得到：

在這個過程中，對於下標 \(0 \le k \lt n\) 告訴我們，左閉右開區間一般比閉區間更好處理！

但是這個過程並不完美，因為我們沒有考慮到 \(m = -1\) 的情況。

考慮 \(x^{\underline {-1}} = \frac 1 {x + 1}\)，於是我們可以得知 \(\sum_{0 \le k \lt n} k^{\underline {-1}} = H_k \vert_0^n = H_n\) ！

其中 \(H_n = \sum_{1 \le k \le n} \frac 1 k\)，這是一個類似於 \(\ln n\) 的東西，兩者的差值並不會太大。

分部求和

無限微積分中，乘法求導有一個公式：\(D(uv) = u Dv + v Du\)，那麼有限微積分中是否也有類似的產物？

將差分運算元運用在兩個函數上：

如果我們定義位移運算元 \(E = \Delta^{-1}\)，也就是 \(E f(x) = f(x + 1)\)，那麼我們有：

我們重新排布一下兩邊，並且對於各自求一個和，那麼我們就可以得到部分求和法則：

它的作用在於一個和式兩部分不太好求，但是一部分是某一個簡單式子的差分形式，另一部分有著一個簡單的差分形式，那麼我們可以通過這種方式進行嘗試。

我們可以知道，\(f(x) = x\) 有著 \(\Delta f(x) = 1\) 的優秀形式，而 \(\Delta (2^k) = 2^k\)，於是利用部分求和法則：

對於第二部分是一個簡單的等比數列形式，那麼我們可以得知：

現在我們嘗試看另外一個例子：

其中 \(x^{\underline k}\) 有簡單的差分形式，而 \(a^x\) 是 \(\frac {a^x}{a - 1}\) 的差分形式，那麼我們可以化為：

這個式子我們需要保證 \(k \ne 0\) 才是正確的，否則，\(n^{\underline k} a^n\) 應當寫為 \(n^{\underline k} a^n - 0^{\underline k} a^0\) 以避免分討。

此時我們發現後半部分的式子是一摸一樣的，所以考慮設 \(S_k = \sum_0^n x^{\underline k} a^x \delta x\)，那麼根據上式，我們有：

其中，若 \(k = 0\) 時，有 \(S_0 = \sum_0^n a^x \delta x = \frac {a^n - 1}{a - 1}\)，於是我們可以 \(O(k)\) 的遞推求出這個式子。

我們可以嘗試進行展開：

得到了其較為簡單的非遞迴式，然而其是否存在封閉形式？目前看來並沒有。

小練習：

第四章 - 數論

階乘的因子

常見的問題為 \(n!\) 中有多少個因子 \(p\)。

我們常見的想法是考慮有 \(k\) 個因子 \(p\) 的數有多少個，但是這是不好算的，考慮至少有 \(k\) 個因子的有多少個。

簡單的，顯然的，這就是 \(\lfloor \frac n {p^k} \rfloor\)，於是乎恰好有 \(k\) 個因子的數有 \(\lfloor \frac n {p^k} \rfloor - \lfloor \frac n {p^{k + 1}} \rfloor\)，於是我們得到式子：

這太醜陋了，小小展開，我們其是就發現更簡單的形式：

有了這個，或許我們就可以證明 Kummer 定理了：

注意到 \(n!\) 中 \(p\) 的次數為 \(\sum_{i = 0} \lfloor \frac n {p^i} \rfloor\)

於是對於 \(\binom{n + m}{m} = \frac {(n + m)!}{n! m!}\)

因子的個數為 \(\sum_{i = 0} \lfloor \frac{n + m}{p^i} \rfloor - \lfloor \frac{n}{p^i} \rfloor - \lfloor \frac{m}{p^i} \rfloor\)

也就是說只有 \(n + m\) 在這裡進位了才能逃離被刪除的宿命……並且由此還可以證明其因數 \(p\) 的個數不超過 \(\log_p (n + m)\)。

互素

在書上的典型結構是 Stern-Brocot 樹。它大概長這樣：

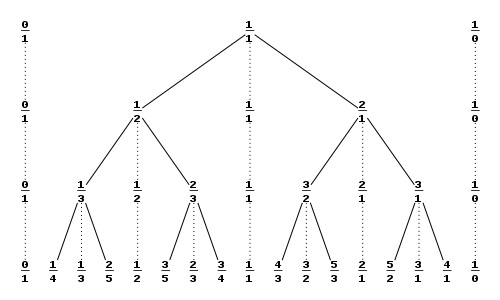
每次得到的新的分數是由左右兩個祖先 \(\frac m n, \frac {m'} {n'}\) 拼湊而來：\(\frac {m + m'}{n + n'}\)

如果繼續觀察，每一層相鄰的兩個數 \(\frac m n, \frac {m'} {n'}\) 一定滿足：

這意味著一定滿足 \(\frac m n < \frac {m'} {n'} \iff m' n - m n' > 0\)（因為這裡保證 \(n > 0\)）

這意味著如果我們有其相鄰的分數的資訊，我們就可以找到它。

我們可以通過矩陣的形式來表示：

我們考慮向左一步，那麼左側的不變，右側的變成自己：

向右一步則是左側變成自己，右側不變：

於是我們可以簡單的二叉搜尋出某個分數在樹上的位置。

第五章 - 二項式係數

二項式係數有很具體的用處，但是想要用好卻不是那麼容易。

比較細緻的文章：# 二項式係數 - zhiyangfan 的小窩

主要是變化太多了，啥都能套一套。

我們對書中部分公式進行證明。

\((5.1)\) 是範德蒙德折積，典。

\((5.2)\) 是利用了恆等變換的範德蒙德折積，前提是 \(t \ge 0\)。

原文中 \((5.3)\) 的證明利用了對於 \(s\) 的歸納法，這裡嘗試給出變換性的證明。

但是這個變化步驟中有很大的漏洞：

• 在第一步 \(\binom {t + k}{n} \to \binom {t + k}{t + k - n}\) 的過程中，我們並沒有關注 \(t + k \ge 0\) 的條件，同樣，在最後我們也沒有關注 \(t + m \ge 0\) 的條件。

但是我太菜了，只能想到如此推導了……

上文是我自己思考的結果……QwQ
感謝 @British_Union 的提示
並感謝 @myee 給出的另一種證明的方法：多項式推理法。

我們發現如果我們能夠保證 \(t > m\)，那麼上述的問題都將不復存在，我們可以合理的如此推導。

而多項式推理法指的是我們可以發現如果 \(n, m, s\) 確定，那麼這是一個關於 \(t\) 的 \(n - s\) 次多項式：

對於等式左側， 我們可以確定是其也是關於 \(t\) 的一個 \(n\) 次多項式，兩者在滿足 \(t > m\) 時相減存在無窮的零點，意味著相減後我們得出的多項式為常數多項式 \(f(x) = 0\)，意味著兩邊相等。

於是我們可以合理的推出這個式子在 \(t\) 作為變數的情況下對於全體實數成立。

剩下的兩個式子推導和這個是一樣的套路，不再展開。

我們順便多學習一下多項式推理法。

在正整數下，我們瞭解到帕斯卡恆等式的成立：

我們可以知道兩側都是關於 \(r\) 的 \(k\) 次多項式，相減也一定是一個 \(k\) 次多項式。

而一個 \(d\) 次多項式至多有 \(d\) 個零點，所以兩個 \(d\) 次多項式相減有兩種情況：

• 至多 \(d\) 個零點，這意味著兩者不盡相等。
• 無窮多個零點，此時相減出來的多項式正是 \(f(x) = 0\)。

我們在此可以瞭解到在 \(\Z_+\) 下等式成立，意味著減出來有無窮多個零點，也就意味著兩者相等！

於是我們可以瞭解到這個恆等式在 \(r \in \R\) 下成立！

來到新的挑戰：

顯然的我們利用三項式變化一下：

利用 \(\binom nm = \frac nm \binom {n - 1}{m - 1}\) 我們可以幹掉 \(k + 1\)：

對於內部來說，我們可以利用恆等變換，再利用 \((5.3)\) 的結果：

但是事實上這裡也有同上的漏洞，\(\binom {n + k} k\) 中 \(n + k\) 可能 \(< 0\) 使得恆等變化後原本沒有值的地方有了值，但是我們需要保證 \(k \ge 0\)，所以上面的變換不盡正確！

所以換一個嘗試：

也就是當 \(n = 0\) 非 \(0\)，即原式等價於 \([n = 0]\)。

通過如上兩個例子，我們發現對稱恆等式確實是一個陷阱……能別用就別用，除非能保證上指標 \(\ge 0\)。

我們進入作業題，對於整數 \(n, m \ge 0\)，求出：

看著好恐怖，\(j\) 出現了 \(4\) 次！還有兩個和式！不過這都是小問題。

我們嘗試一點一點消掉他們。

首先觀察到 \(\binom {-j + rk + s}{m - j}\) 上下都有 \(-j\)，嘗試利用上指標反轉幹掉一個：

我們發現在 \(k\) 已知的情況下，這就類似一個範德蒙德折積！於是改變求和順序：

考慮外面有一個 \((-1)^m\)，內部的下指標都是 \(m\)，那麼都反轉一下，順便將剩下的 \(-1\) 乘進去：

稍微平移一下下標：

於是我們就得到了這個簡單的封閉形式。

高階差分與牛頓級數

這在 math 1.4 中講了，內容參見 share-math。

第六章 - 特殊的數

斯特林數

斯特林數分為第一類和第二類。比較常用的是第二類。

第二類斯特林數 \(n \brace k\) 的組合意義為講 \(n\) 個物品的集合劃分為 \(k\) 個非空子集的方法數。

利用這個意義我們可以引出一個遞推式：

分別指的是新開一個子集，或者放入某一個子集的方案數。

對於第一類斯特林數，其還對於每一個子集排成了環，形成了 \(k\) 個輪換（cycle）

對於每一個大小為 \(m\) 的子集，存在 \((m - 1)!\) 種輪換，由此可以看出存在 \({n \brack k} \ge {n \brace k}\)。

我們同樣可以通過組合意義找到一個遞推式：

分別指新開一個輪換，或者插入到某一個元素前面。

有了加法公式，那麼很多時候我們就可以通過歸納法證明與之相關的內容了。

在這之前，我們可以討論一下 \({n \brack k}\) 與排列的關係。

輪換加排列在組合數學中有另外一個體現：置換。

置換可以將一個排列劃分為若干個有向圈，每一個有向圈對應著某一個輪換。

這意味著每一個排列都對應著一個子集輪換的方案，換言之：

我們回到加法公式和歸納法上，關於 \(n \brace k\) 有一個非常經典的等式：

我們一定可以通過歸納法證明它，考慮 \(x \times x^n = x^{n + 1}\)，或許我們能夠對 \(n\) 進行歸納證明之。

先考慮 \(n = 0\) 的情況，\(LHS = 1\)，而 \(RHS = {0 \brace 0} x^{\underline 0} = 1\)，故 \(n = 0\) 的時候成立。

對於 \(x^{n + 1}\)，我們如此考慮歸納：

我們考慮 \(x \times x^{\underline k}\) 是否有很好的表達方式，發現可以通過 \(x^{\underline {k + 1}} = x^{\underline k} (x - k)\) 得出：

於是我們可以簡單的將上式拆開：

於是歸納得證。

斯特林數有許許多多不那麼常用的恆等式，所以並不太需要注意。

不過我們回到加法公式：

我們是否能夠像：

一樣將他們推廣到更多的地方？

事實上，如果我們先約定 \({0 \brace k} = {0 \brack k} = [k = 0]\) 以及 \({k \brace 0} = {k \brack 0} = [k = 0]\)，那麼我們就可以利用加法公式求出負數下 \({n \brace k}\) 的值！

如果將整個表畫出來，那麼我們將得到一個驚人整齊的等式：

這容易利用加法公式驗證。

第一類斯特林數並沒有通項公式，但是第二類斯特林數卻存在。

可以通過二項式反演簡單的證明：

或者寫成稍微好看的一個形式：

當這個形式一出來，那麼我們就可以知道如何快速的求一行斯特林數了。

設 \(F(x) = \frac {x^n}{i!}\)，\(G(x) = \frac {(-1)^x} {x!}\)，那麼知道：

於是我們可以通過 NTT \(O(n \log n)\) 的求出整行的第二類斯特林數。

我們現在考慮是否能夠快速的求出整列的斯特林數？

我們考慮一列斯特林數的生成函數：

根據加法公式，我們有：

於是存在：

於是我們得到：

於是可以分治 NTT 和多項式取逆做即可。

然而實際上有辦法避免多項式求逆的，但是有點複雜。

但是不合理，程式碼太抽象了，我們換一個方法，考慮 EGF。

將斯特林數拆開：

於是多項式快速冪即可。這隻需要寫一個 NTT 即可做到 \(O(n \log n \log k)\)。

其實通過類似的方式，我們可以推匯出第一類斯特林數行列的求法。

這裡不做過多展開。

調和數

調和數 \(H_n = \sum_{i = 1}^n \frac 1i\)，認為是離散下對於 \(\ln n\) 的模擬，其誤差 \(\gamma \approx 0.577215\)。

這是尤拉所證明的：\(\lim\limits_{n \to \infty} (H_n - \ln n) = \gamma\)。

對於調和數我們還有一個與斯特林數掛鉤的等式：

考慮通過：

可以知道：

於是只需要展開這個遞迴式即可得到 \((6.1)\)。

第一個例題較好，複習了分部求和法則：

如果掌握的分部求和法則，那麼這就比較簡單，這裡不再展開。

我們總是會遇到它的生成函數的，雖然這是之後的內容（也是後面回來寫的）

學完生成函數和折積以後，我們會了解到一個小技巧：生成函數字首和。

具體來說，對於 \(\langle f_n \rangle\) 與 \(\langle 1, 1, \cdots \rangle\) 的折積會得到 \(\langle \sum_{i = 0}^n f_i \rangle\)。

在生成函數上的體現便是 \(F(x) \to \frac 1 {1 - x} F(x)\)。

我們可以利用這個技巧快速的算出 \(H_k\) 的生成函數。

考慮 \(H_n = \sum_{i = 1}^n \frac 1 i\)，那麼實際上它就是 \(\langle 0, 1, \frac 12, \frac 13, \cdots \rangle\) 的字首和。

後者實際上為 \(\ln \frac {1}{1 - x}\)，於是我們可以知道 \(H_n\) 的生成函數為：

斐波那契數

斐波那契數由如下遞迴式定義：

我們容易通過歸納法證明：

同樣，也可以通過矩陣乘法證明，參見 # 演演算法學習筆記(37): 矩陣

由此我們可以推出：

可以通過 \((6.2)\) 和歸納法簡單的證明。

於是我們可以知道：

線性遞推

斐波那契數列衍生而出的另一個知識叫做遞推，而遞推就可以講到線性齊次遞推和非齊次遞推。

或許我們需要先學會生成函數？

對於形如：

定義其特徵方程為：

根據代數基本定理，上式有 \(k\) 個根 \(q_1, q_2, \cdots, q_k\)，我們稱之為特徵根，那麼：

在下述意義下是原遞推關係的通解：

換句話來說，是通解意味著對於任意給定的初值，都可以解出如下方程組：

而此方程組的係數矩陣為：

這顯然是一個範德蒙德矩陣，其行列式為：

也就是說，我們需要保證根互不相同，使得矩陣滿秩（行列式不為 \(0\)）才可以求出唯一解。

然而實際上有另外一種利用生成函數的方法，更加簡明。

繼續沿用斐波那契數列的例子 \(f_n = f_{n - 1} + f_{n - 2}\)。

設 \(F(x) = \sum_{i \ge 0} f_i x^i\) 是其生成函數。

根據遞推關係，我們可以得出 \(F(x) = xF(x) + x^2F(x)\)。

具體來說，三個生成函數對應的序列如下：

於是 \(F(x) = \frac 1 {1 - x - x^2}\) 得出也就很自然了（當然這是錯誤的。

真的自然嗎？我們是不是忘了什麼東西？

確實，我們忘了一些東西，我們重新將三者寫下來：

也就是說 \(F(x) - xF(x) - x^2F(x)\) 實際上 \(= f_0 + (f_1 - f0)x\)！

將初始值 \(f_0 = 0, f_1 = 1\) 帶入，我們才真正地正確地得到其生成函數：

如果我們得到了生成函數，我們是否能夠確定其通項公式？答案是可以的。

我們將 \(\frac x {1 - x - x^2}\) 稍微分解 \(= \frac {c_1}{x - \frac {-1 + \sqrt 5}{2}} + \frac {c_2}{x - \frac {-1 - \sqrt 5}{2}}\)。

可以列出方程簡單的求解出 \(c_1, c_2\) 是什麼。

我們通過 \(\frac 1 {1 - x} = \sum_{i \ge 0} x^i\) 各項展開，於是就可以得到其通項公式！

我們現在看看 \(\frac {1 + \sqrt 5}{2}\) 以及 \(\frac {1 - \sqrt 5}{2}\) 這兩個數。

我們賦予了其一個符號，足以可見其重要程度：\(\phi = \frac {1 + \sqrt 5}2, \hat \phi = \frac {-1} \phi = \frac {1 - \sqrt 5} 2\)。

這兩個數是 \(1 - x - x^2 = 0\) 的根，故我們有：

我們通過這兩個符號將 \(F(x)\) 寫出來：

這形式很優美，我們之後將會用到。

通過冪級數展開，我們就得到了 \(f_n\) 的通項公式：

奇妙的是一堆 \(\sqrt 5\) 乘起來就變成了一個整數！

來到更大的挑戰：

我們是否能夠找到其通項公式？

從特徵根考慮：\(x^2 - 4x + 4 = 0 \to (x - 2)^2 = 0\)。

此時 \(2\) 作為根出現了兩次，我們稱之為二重特徵根，在此情況下 \((6.3)\) 退化成了：

然而這並不是我們想要的，因為對於給定的 \(h_0 = a, h_1 = b\)，我們不一定能夠滿足：

所以我們需要另闢蹊徑。

我們很容易知道 \(h_n = 2^n\) 是其一個解，我們也可以證明 \(h_n = n 2^n\) 是一個解。

為了尋找通解，我們可以斷言：

是這個遞推式的通解！

我們進行驗證，對其施加 \(h_0 = a, h_1 = b\) 的初始條件，那麼：

我們總是有解！於是這可以作為其通解。

我們可以合理外推，從而找到一個更一般的結論。

對於非齊次線性遞推，一般來說，利用生成函數會更為方便。這裡舉例說明。

設其生成函數 \(F(x)\)，根據遞推關係，我們有：

於是

我們知道：

於是我們知道：

於是，我們便可以通過拆分這一個函數求解出其通項：

生成函數立大功！

第七章 - 生成函數

無限微積分

生成函數與高等數學強相關，確實需要部分知識，這裡寫下以便參考。

關於求導：

關於泰勒展開（這是在 \(0\) 處的展開，我們用的最多）：

解遞迴式

我們線上性遞推那裡已經看到了生成函數的重要性，我們是否能夠找到一個基本方法以求解出任何遞推式？

答案是可以的，並且這個方法相當的機械：

1. 將遞迴式寫成關於 \(h_n\) 的單個方程，在假定 \(h_{-1} = h_{-2} = \cdots = 0\) 的情況下對於任何正整數成立！
2. 將他改寫為生成函數 \(F(x)\) 之間的關係。
3. 解得到的生成函數 \(F(x)\)，將之表示為封閉形式。
4. 展開 \([x^n]F(x)\)，得到 \(g_n\) 的封閉形式。

前面的步驟在上文的鋪墊中應該十分清晰了，然而對於第四步，我們可能還有技巧上的困難。

一般來說，我們需要通過強硬的分解，將生成函數表示為：

從而得出很好的係數：

然而難點並不是在這一步，而是強硬分解出 \(c_i\) 的那一步 QwQ

我們可能更多的只能依靠人類智慧完成。

我們來一個很好的例子：

我們將之寫成一個式子：

於是可以將之改寫為生成函數之間的關係：

我們可以稍微變化一下這個式子：

於是得到：

於是暴力展開即可得到通項：

折積

對於給定的兩個數列 \(\langle f_n \rangle\) 以及 \(\langle g_n \rangle\) 的折積 \(\langle h_n \rangle\)，我們有：

注意到數列的折積和生成函數的乘積對應，那麼對於許多式子，我們就有很好的方法利用折積處理了。

斐波那契數列折積

是的，還是斐波那契數列，它具有十分重要的地位，它足夠簡單，也足夠複雜。

我們嘗試計算 \(\sum_{k = 0}^n f_k f_{n - k}\) 的封閉形式，這是 \(\langle f_n \rangle\) 與自身的折積。

正常來說，我們直接可以利用 \(F(x) = \frac x {1 - x - x^2}\) 的平方 \(F(x)^2 = \frac {x^2}{(1 - x - x^2)^2}\) 然後展開求解其通項，但是這比較複雜，並沒有更好的用到斐波那契和折積。

我們嘗試利用另一個生成函數：

中間關於 \(\frac {1}{(1 - \phi x)(1 - \hat \phi x)}\) 的化簡我們再從一個生成函數入手：

考慮 \(\phi \hat \phi = -1\)，我們有：

於是 \(\frac {1}{(1 - \phi x)(1 - \hat \phi x)} = \frac {F(x)} x - \sum_{n \ge 0} f_{n + 1} x^n\)。

接下來我們繼續化簡上述式子，現在難點就在於 \(\sum_{n \ge 0} (\phi^n + \hat \phi^n) x^n\) 怎麼求。

考慮兩者的生成函數：

於是我們嘗試對左式化簡：

於是：

於是我們得到：

於是得到通項公式：

生成函數的勝利！

指數生成函數

我們看看一個好好的例子：

好好好，這麼玩是吧，但是為什麼不用 \(z^{\bar{m}} = \sum_{n \ge 0} {m \brack n} z^n\)？

我們回到正常的 EGF，考慮對於 \(\langle h_n \rangle\) EGF 的操作有哪些影響。

考慮 \(xF(x)\)：

這就是 \(\langle n g_{n - 1} \rangle\) 的 EGF，相當於在 OGF 上求了一次導。

如果需要平移，那麼我們只需要 \(F'(x)\) 或者 \(\int_0^z F(x)\) 即可。

對於指數生成函數的折積來說，生成的數列是 \(\langle f_n \rangle\) 和 \(\langle g_n \rangle\) 的二項折積：

也就是考慮到 \(\binom nk = \frac {n!}{k! (n - k)!}\)：

這可以和伯努利數牽扯起來。

考慮伯努利數的遞迴式：

發現這就是 \(\langle B_n \rangle\) 和 \(\langle 1, 1, \cdots \rangle\) 的二項折積。

所以我們得到其指數生成函數為 \(\frac z {e^z - 1}\)。

指數生成函數在組合意義上十分有用，其一個重要的應用於 \(\exp\) 相關。

可以參考：# 淺談 Exp 的組合意義 - 飛雨煙雁 的部落格

更多 \(O(n^2)\) 對於多項式的操作見：# 各種多項式操作的 n^2 遞推

第八章 - 離散概率

期望與方差

期望的線性性以及耳熟能詳了：

值得一提的是這並不要求兩個隨機變數獨立！

對於方差，其基本的定義為：

但是我們可以將之展開：

也就是說：

我們也可以證明：

概率生成函數

感覺沒啥用，咕。

作者有話說

本文共 \(\ge 10000\) 個詞，\(\ge 25000\) 個字元（包括公式），花了 \(3\) 天時間，梳理了具體數學一書中目前對我有用的部分。

有很多的啟示，補全了很多我所未知或者不熟練的東西。

限於時間原因，很多內容我無法細細談論，如果有時間後面再補充（其實也沒啥特別重要的東西了，邊邊角角的

完結撒花★,°:.☆(￣▽￣)/$:.°★ 。